Search

벡터와 벡터 연산

대분류
인공지능/데이터
소분류
AI 수학
유형
선형 대수학
부유형
벡터
벡터 연산
주요 레퍼런스
https://brunch.co.kr/@jennyjang93/42
최종 편집 일시
2024/10/27 15:34
생성 일시
2024/07/15 02:43
13 more properties

벡터

•
크기와 방향을 가진 양을 나타내는 개념
•
화살표(→)로 작성
•
벡터의 크기 : 화살표의 시작점과 끝점 사이의 거리

벡터 표기법

•
단위 벡터
◦
벡터의 크기가 1인 벡터
◦
머리 위에 달린 괄호 모양 = hat
x^\hat{x}
•
일반 벡터
◦
방향과 크기를 갖고 있는 물리량 = 힘 : F = ma
nx^=x→ n\hat{x}=\overrightarrow{x}
•
미분
◦
1번 미분 (dot)
x˙\dot{x}
◦
2번 미분(double dot)
x¨ \ddot{x}
•
벡터의 아래첨자
◦
벡터의 방향이 어느 축 위에 있다면 하단에 축을 기록
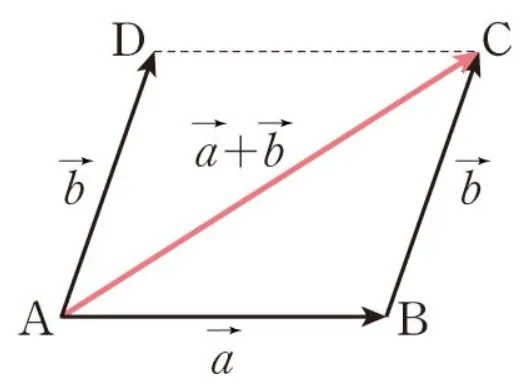
v1→,v2→,v3→\overrightarrow{v_1},\overrightarrow{v_2},\overrightarrow{v_3}

벡터 덧셈

•
두 개 이상의 벡터를 합하는 연산
•
두 개의 n-차원 벡터 u = [u1, u2, … un]과 v = [v1,v2, …, vn]가 있을 때
이들의 합인 w = u + v는 다음 수식으로 정의
w=u+v=[u1+v1,u2+v2,...,un+vn]w = u + v = [u1+v1, u2+v2, ...,un+vn]
<전제 조건> 해당 u와 v는 같은 차원을 가지고 있어야 함 벡터 덧셈은 각 요소들을 각각 더하는 연산 각 요소가 더해진 결과인 로운 벡터 w도 같은 차원을 가짐
•
예시
◦
2-차원 벡터 [1,3]과 [4,2]를 더하면 [1+4, 3+2] = [5,5]
◦
이는 좌표 평면 상에서 원점에서부터 각각 (1,3)과 (4,2)만큼 떨어져 있는 두 점을 연결하는 벡터와 동일
◦
이 두 벡터를 더하면 원점에서 부터 (5,5)만큼 떨어져 있는 점을 지나는 새로운 벡터가 됨

벡터 스칼라곱

•
벡터와 스칼라(실수)를 곱한 결과
•
n-차원 벡터 v = [v1,v2, …, vn]와 스칼라(실수) a가 있을 때, 이들의 스칼라곱인 w = a * v는 다음 수식으로 정의
w=a×v=[av1,av2,...a×vn]w = a × v = [av1, av2, ... a×vn]
•
각 요소들에 스칼라 곱을 곱해주는 연산
→ 벡터 스칼라곱의 결과인 새로운 벡터 w도 같은 차원을 가짐
•
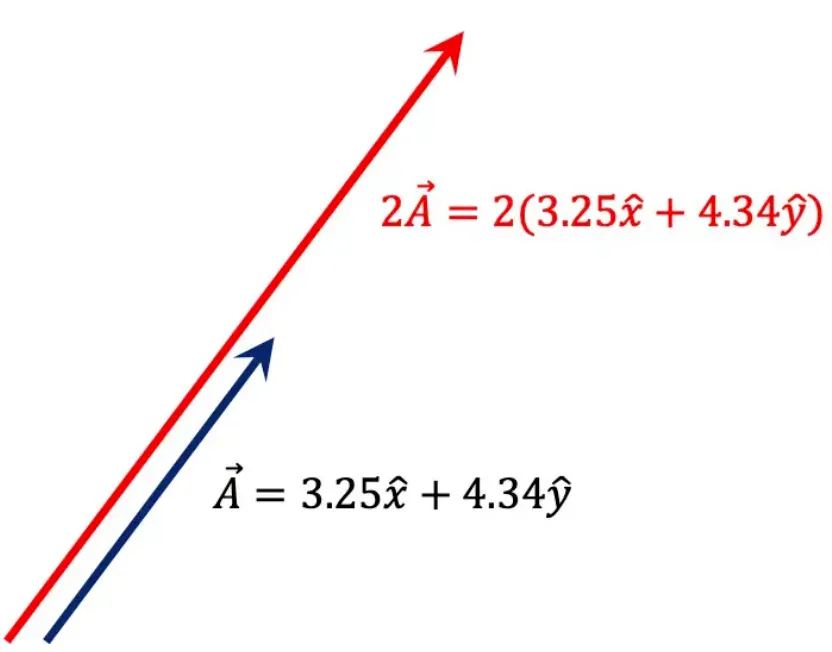
벡터의 크기를 조절하는 역할
◦
a가 양수일 때 : 벡터의 방향은 유지되면서 크기가 증가
◦
a가 음수일 때 : 벡터의 방향이 반대가 되면서 크기가 감소
◦
a = 0일 때 : 벡터의 크기가 0이 되므로, 벡터가 원점에 위치
•
예제
◦
2-차원 벡터 [1,2]와 스칼라 값
▪
2를 곱하면 [2,4] : 이는 원래 벡터 방향을 유지하면서 크기를 2배로 만든 벡터
▪
-1을 곱할 시 [-1,-2] : 벡터의 방향은 반대, 크기는 1배로

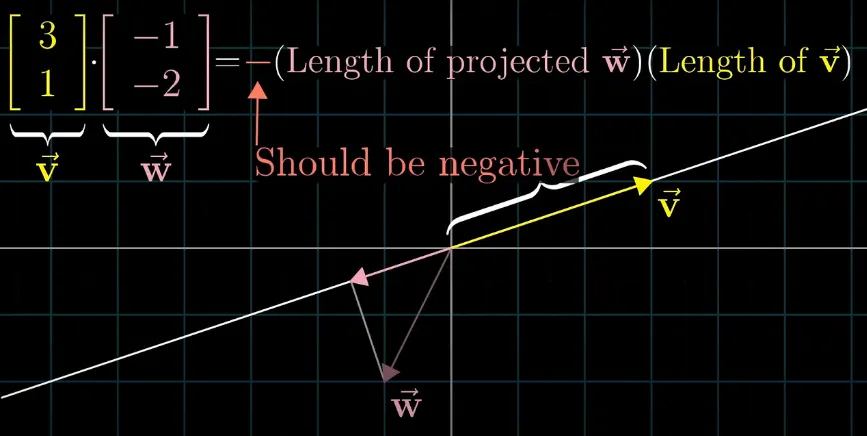
벡터 내적 (Inner product)

•
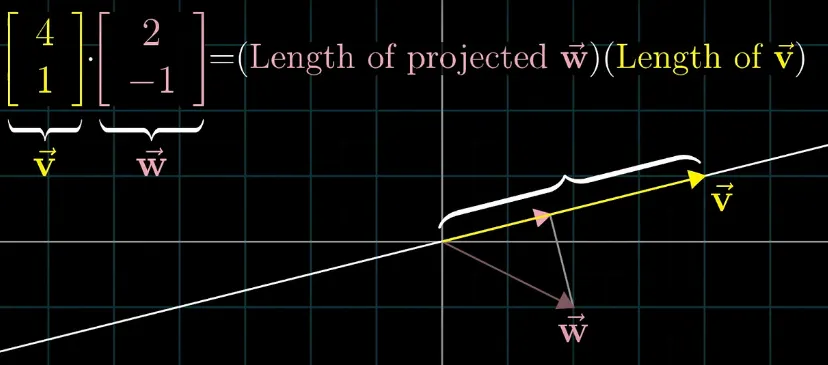
두 벡터의 곱의 합을 구하는 연산 ( · )
•
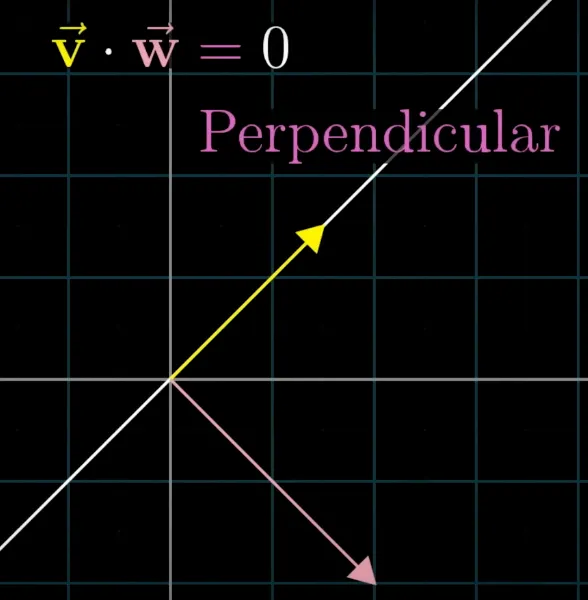
두 벡터 사이의 각도와 크기 정보를 제공
•
n-차원 벡터 u = [u1, u2, …, un]와 v = [v1, v2, … vn]가 있을 때, 이들의 내적 w = u · v는 다음 수식으로 정의
w=u⋅v=u1v1+u2v2+...+unvnw = u · v = u1v1 + u2v2 + ... + un vn
u⋅w=∣∣u∣∣∣∣w∣∣cosθu ·w = ||u|| ||w||cos\theta
◦
ex) [1,2] · [3,4] = (1*3)+(2*4) = 3+8 = 11
•
두 벡터의 내적은 각 차원의 요소들을 곱한 후, 그 곱의 합을 구하는 것
•
벡터 내적은 두 벡터가 이루는 각도와 벡터의 크기 정보를 제공
◦
두 벡터의 내적이 0이면 두 벡터는 수직 (직교)
◦
내적이 양수인 경우 : 두 벡터는 같은 방향을 지침
◦
내적이 음수인 경우 : 두 벡터는 반대 방향을 지침

머신러닝에서의 내적

•
유사도(similarity) 측정
◦
데이터 간의 관계 파악, 분류(클래스피케이션), 군집화(클러스터링), 추천(레코멘디드) 등에 활용
◦
내적 값이 클수록 두 벡터는 유사하다는 것을 의미
•
회귀 분석(regression analysis)
◦
입력 변수(input features)와 출력 변수(target variable)간의 선형 관계 모델링
◦
벡터의 내적은 입력 변수와 가중치(weight)간의 연산으로 이루어짐 → 예측 모델 학습
•
차원 축소
◦
고차원 데이터(high-dimensional data)를 저차원 공간(low-dimensional space)으로 축소하여 데이터를 시각화하거나 분석에 활용
◦
차원 축소 기법 중 주성분 분석(PCA: Principal Component Analysis)에서 사용
•
커널 기법
◦
비선형 문제 해결 방법
◦
커널 함수(kernel function)는 입력 데이터 간의 유사도를 측정하여, 비선형 문제를 선형 문제(linear problem)으로 변환
◦
이 때 커널 함수는 벡터의 내적 연산으로 계산

벡터 외적(Cross product)

•
두 개의 벡터를 이용하여 수직인 방향의 새로운 벡터를 생성하는 연산
•
벡터의 외적은 다음 수식으로 정의
∣a×b∣=∣a∣∣b∣sinθ| a ×b| = |a||b| sin\theta
a×b=−b×aa×b = -b×a
a×b=c(수직인벡터)a×b=c(수직인 벡터)
◦
|a×b|는 벡터 a와 b가 이루는 평면의 면적
◦
θ는 벡터 a와 b가 이루는 각도
•
외적의 특징
◦
벡터의 크기가 아닌 벡터의 방향 계산
◦
외적 결과는 두 벡터가 이루는 평면에 수직인 방향을 지침
◦
벡터의 외적은 3차원 벡터에 대해서만 정의 (2차원은 적용되지 않음)

내적과 외적의 차이

내적
외적
계산
두 벡터의 크기와 두 벡터가 이루는 각도에 따라 스칼라 값을 계산
두 벡터가 이루는 평면에서 수직인 벡터 계산
결과값
스칼라
벡터
차원
두 벡터의 크기가 같은 n-차원
only 3-차원