Search

RNN

대분류
인공지능/데이터
소분류
ML/DL 정리 노트
유형
딥 러닝
부유형
NLP Pytorch
최종 편집 일시
2024/10/27 15:22
생성 일시
2024/10/02 00:30
14 more properties

First Order System

•
현재 시간의 상태가 이전 시간의 상태와 관련이 있다고 가정

이전 시간의 상태만 입력으로

•
Autonomous System
•
외부 입력 없이 자기 혼자서 돌아가는 특징을 보유
xt=f(xt−1)x_t = f(x_{t-1})
◦
xx : 상태, 피처
◦
tt : 시간
◦
xtx_t: t시간일 때의 상태
◦
xt−1x_{t-1}: t-1시간(바로 직전, 이전 시간)일 때의 상태
•
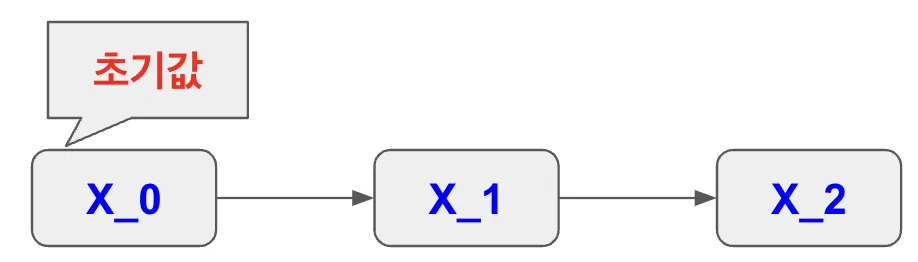
이전 시간의 상태만 입력으로
◦
X0X_0: 초기값, 시스템의 시작 상태, 이 값으로부터 시스템의 동작이 시작
◦
X1X_1: 첫 번째 시간 단계에서의 상태, 이 값은 바로 이전 상태인 X0에 의해서만 결정
◦
X2X_2: 두 번째 시간 단계에서의 상태, 이 값은 이전 상태인 X1을 기반으로 결정

이전 시간의 상태와 현재 값을 입력으로

•
어떤 시스템이 현재의 상태를 결정할 때, 그 상태는 이전의 상태와 현재의 입력 값에 의해 결정된다는 것
•
상태가 이전 상태와 현재 입력에 의존하는 시스템을 이용하면, 복잡한 동작을 가진 시스템의 동작을 예측하거나 제어하는 데 큰 도움이 된다.
xt=f(xt−1,ut)x_t = f(x_{t-1},u_t)
◦
xx : 현재의 상태 (t 시점에서의 상태)
◦
tt: 시간
◦
utu_t: 현재의 입력 (t 시점에서 시스템에 가해진 입력).
◦
xtx_t: t시간일 때의 상태
◦
xt−1x_{t-1}: 이전 시간의 상태 (t-1 시점에서의 상태).
◦
ff : 현재 상태를 계산하는 함수, 즉 시스템의 동작을 설명하는 수학적 규칙.
•
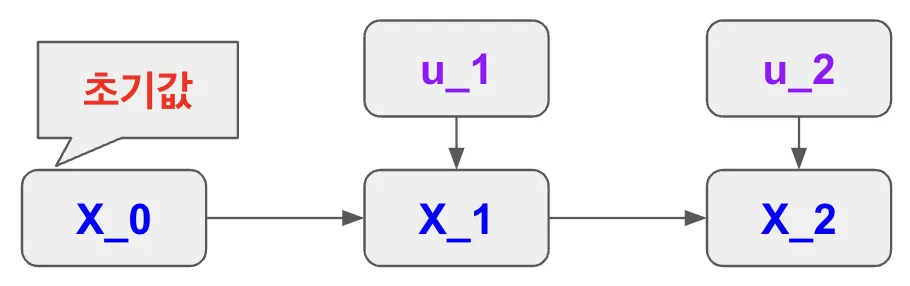
이전 시간의 상태와 현재 값을 입력으로
◦
X0X_0: 초기값, 시스템의 시작 상태, 이 초기 상태로부터 시스템의 동작이 시작
◦
X1:X_1: 첫 번째 시간 단계에서의 상태, 이 값은 이전 상태 X0와 첫 번째 입력 값 u1의 영향을 받아 결정
→ 즉, 이전 상태뿐만 아니라 현재 입력이 상태 변화에 영향을 미치는 것
◦
X2X_2: 두 번째 시간 단계에서의 상태, 이전 상태 X1과 두 번째 입력 값 u2에 의해 결정
◦
X_0(50%)와 U_1(50%)에 대한 학습 정보 → X_1
◦
X_1(50%)와 U_2(50%)에 대한 학습 정보 → X_2
◦
최종 : X_0(25%)와 U_1(25%)과 U_2(50%)에 대한 학습 정보 → X_1
→ 단점 : 비율이 다름, 맨 처음 학습 정보

상태 공간 모델(State-Space Model)

•
1차원 시스템의 모형(First Order System)
xt=f(xt−1,ut)x_t = f(x_{t-1}, u_t)
◦
utu_t: t시간일 때의 현재(입력) 값
◦
xt−1x_{t-1}: t-1시간(이전 시간)일 때의 상태
•
각 시간에서 관측 가능한 상태($x_t$)의 모음
yt=h(xt)y_t = h(x_t)
◦
xx: 상태(hidden layer의 state)
◦
tt: 시간
◦
xtx_t: t시간일 때의 상태
◦
yty_t: t시간일 때의 출력 값
◦
h()h(): 활성화 함수
•
상태 업데이트: 현재의 상태는 이전 상태와 현재 입력에 의해 결정된다.
◦
수학적으로는 다음과 같은 식으로 표현할 수 있다: xt=f(xt−1,ut)x_t = f(x_{t-1}, u_t)
◦
여기서 ff는 시스템의 특성을 결정하는 함수, 이 함수는 선형일 수도 있고 비선형일 수도 있다.
•
출력 계산: 현재의 출력은 현재의 상태에 의해 결정된다.
◦
이를 수학적으로 표현하면: yt=g(xt)y_t=g(x_t)
◦
여기서 gg는 상태에서 출력을 계산하는 함수, 이 출력 함수는 시스템의 관찰 가능한 결과를 나타낸다.
•
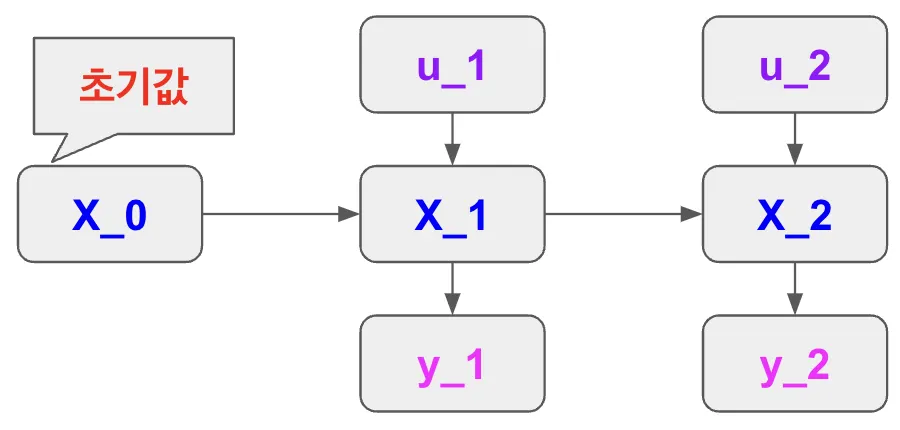
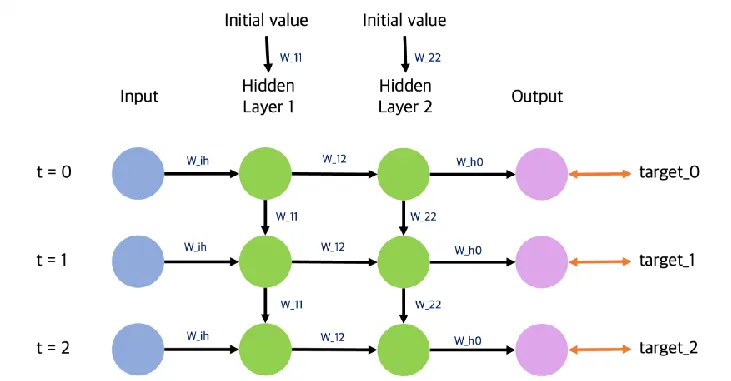
State-Space Model 구조
◦
X0X_0: 초기 상태, 시스템의 시작 상태, 여기서 시스템이 어떤 상태에서 시작하는지 결정되며, 이 상태를 기반으로 이후의 상태가 계산
◦
u1u_1, u2u_2: 각 시간 단계에서 주어지는 입력 값, u1u_1은 첫 번째 시간 단계에서, u2u_2는 두 번째 시간 단계에서 시스템에 영향을 미치는 외부 자극이나 제어 신호
◦
X1X_1, X2X_2: 시스템의 상태(state), 예를 들어, X1은 첫 번째 시간 단계에서의 상태이며, 이는 이전 상태인 X0X_0과 현재 입력인 u1u_1에 의해 결정, 마찬가지로, X2X_2는 X1X_1과 u2u_2에 의해 결정
◦
y1y_1, y2y_2: 각 시간 단계에서의 출력(output), y1y_1은 상태 X1X_1에 의해 결정되며, 시스템이 외부로 나타내는 결과물, y2y_2는 상태 X2X_2에 의해 결정되는 출력

RNN(Recurrent Neural Networks) : 순환 신경망

•
시계열 데이터나 순차적인 데이터를 처리하고 분석하는 데 특화된 인공지능 모델
•
이전의 상태를 기억하고, 그 정보를 이용해 다음 출력을 생성할 수 있다.
•
입력받는 신호의 길이가 한정되지 않은 동적 데이터를 처리
•
CNN vs RNN
◦
CNN은 이미지 구역별로 같은 weight를 공유
◦
RNN은 시간별 같은 weight를 공유

특징

•
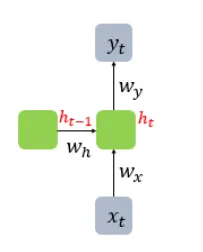
hth_t는 tt일 때의 hidden layer 상태를 나타낸다.
•
hth_t는 이전까지의 상태(h0,ht−1h_{0}, h_{t-1})와 이전까지의 입력(xt−1,xtx_{t-1}, x_t)을 대표할 수 있는 압축본이라고 할 수 있다.
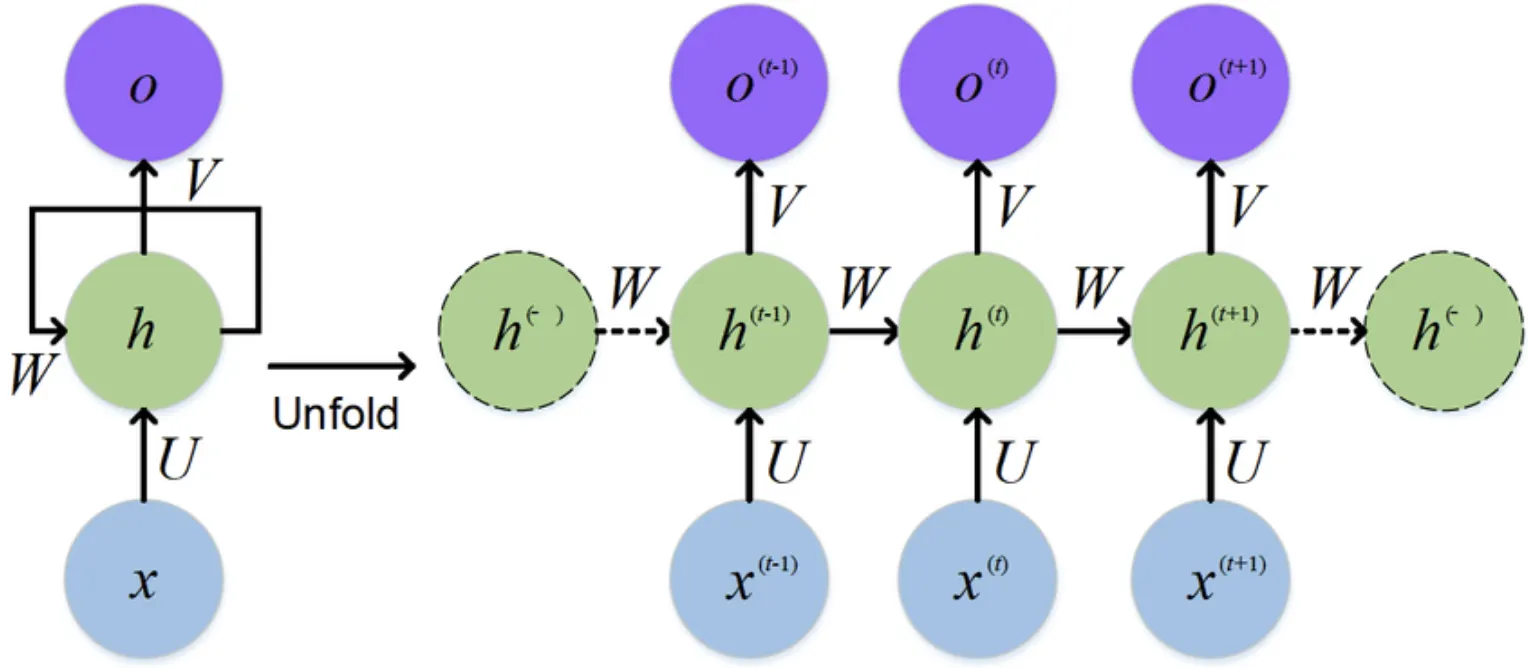
왼쪽: RNN 셀 (Fold)
오른쪽 :시간에 따른 RNN의 펼친 모습 (Unfold)
◦
레이어는 2개
◦
유닛은 3개
◦

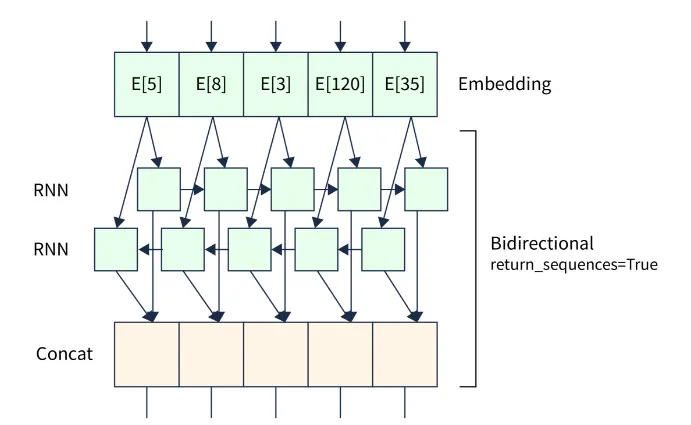
Bi-directional RNNs

Back propagation in RNN (역전파 과정 - 순환 신경망)

시계열 데이터 학습 수행

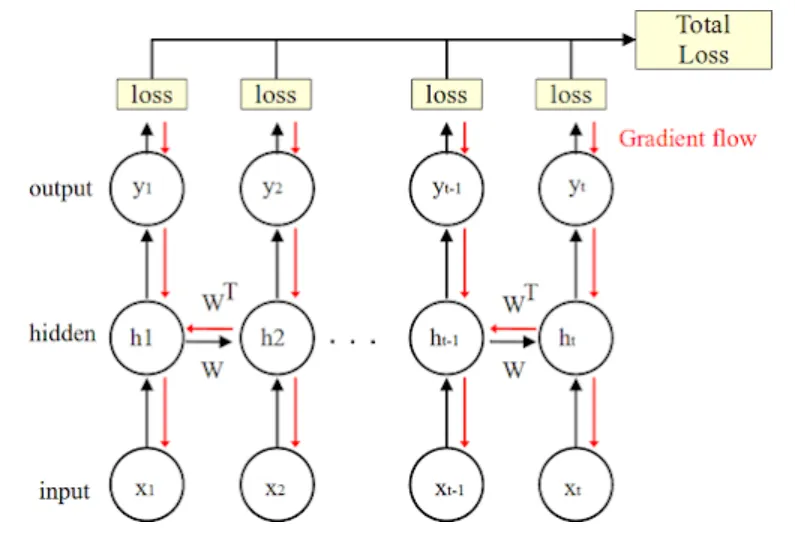
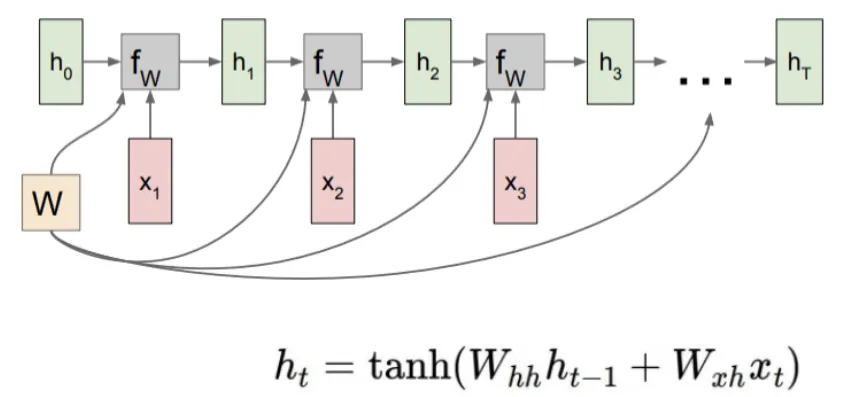
1. RNN의 시간적 확장

•
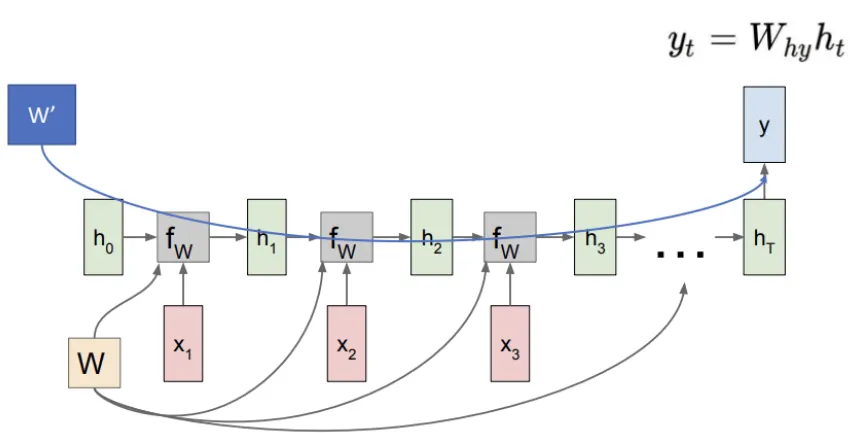
그림에서는 RNN이 시계열 데이터를 처리하기 위해 시간 축을 따라 펼쳐진 형태로 표현되어 있다. RNN은 동일한 가중치 W를 각 시간 단계에서 공유하며, 이는 신경망이 같은 파라미터를 여러 시간 단계에서 반복적으로 사용하는 특징을 나타낸다.
WW
•
입력 (x1,x2,…,xtx_1, x_2, \ldots, x_tx1​,x2​,…,xt​): 입력 데이터가 각 시간 단계에 걸쳐 순차적으로 들어온다.
•
은닉 상태 (h1,h2,…,hth_1, h_2, \ldots, h_th1​,h2​,…,ht​): 이전 은닉 상태와 현재 입력을 결합하여 새로운 은닉 상태를 생성한다.
•
출력 (y1,y2,…,yty_1, y_2, \ldots, y_ty1​,y2​,…,yt​): 각 은닉 상태에서의 출력 값을 통해 특정 작업을 예측하거나 계산한다.

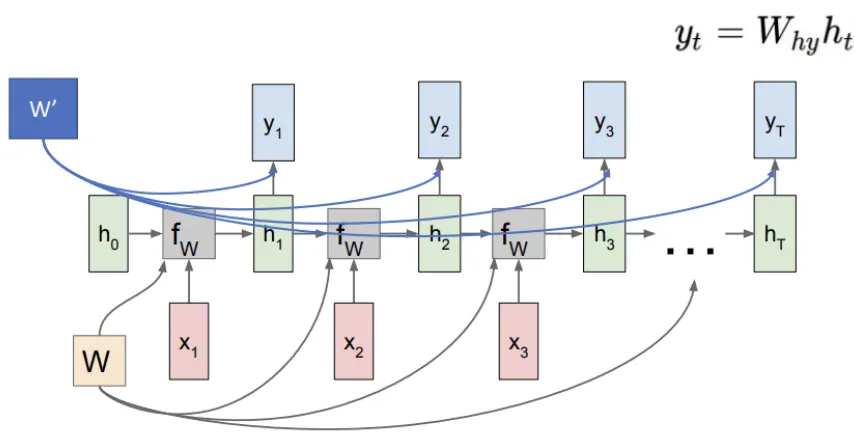
2. 손실 함수와 역전파

•
각 시간 단계에서 **손실(loss)**이 계산되며, 최종적으로 **총 손실(Total Loss)**로 결합된다. 이 총 손실은 모든 시간 단계의 손실을 합산한 값이다.
•
역전파(Backpropagation Through Time): 손실을 최소화하기 위해 BPTT 방식을 통해 가중치를 업데이트한다. 역전파는 시간의 역순으로 이루어지며, 현재 시점의 오류를 이전 시간 단계로 전파하여 가중치 W에 대한 그래디언트를 계산한다.
WW
◦
그림에서 빨간색 화살표는 그래디언트가 흐르는 방향을 나타낸다. 이는 각 손실이 은닉층과 가중치로 다시 전파되어 가중치를 업데이트하는 과정이다.

3. 가중치 공유 및 그래디언트 소실 문제

•
모든 시간 단계에서 가중치 WW는 공유되므로, 이 가중치를 업데이트하기 위해 각 시간 단계에서 역전파를 통해 그래디언트가 전파된다.
•
RNN에서 Gradient Flow는 연쇄적인 그래디언트 계산으로 인해 그래디언트 소실(Vanishing Gradient) 또는 그래디언트 폭발(Exploding Gradient) 문제가 발생하기 쉽다.
그래디언트 소실/폭발(Exploding/Vanishing Gradient) : 시계열이 길어질수록 그래디언트가 점점 더 작아져서 모델이 과거의 정보를 학습하기 어려워지는 현상

4. 시간 단계의 역전파

•
BPTT는 역전파 알고리즘의 변형으로, RNN의 모든 시간 단계에 걸쳐서 손실의 그래디언트를 계산하는 과정이다.
•
예를 들어, h2h_2에서의 손실은 h1h_1의 영향을 받고, 이 과정이 반복적으로 이전 시간 단계로 거슬러 올라가면서 각 시간 단계에서의 손실 기여도를 반영하여 가중치를 업데이트한다.

5. 그래디언트 흐름과 가중치 업데이트

•
WW와 WTW^T의 업데이트는 모든 시간 단계의 손실에 대한 합에 의해 영향을 받는다. 이러한 구조 때문에 RNN은 긴 시간 의존성을 학습하는 데 한계가 있을 수 있으며, 이를 해결하기 위해 LSTM이나 GRU 같은 개선된 구조가 개발되었다.

구조 종류

•
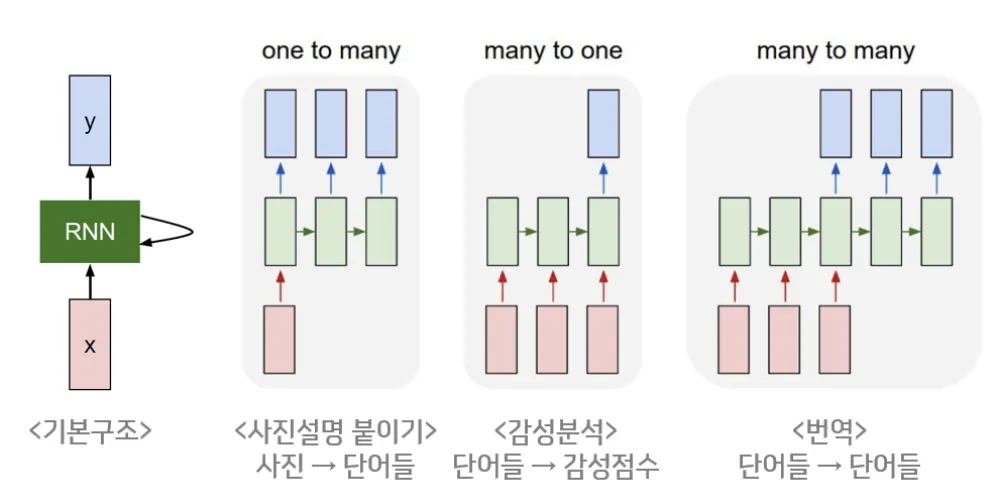
기본구조
•
One-to-Many (사진 설명 붙이기)
◦
하나의 입력이 주어지면 여러 개의 출력이 나오는 구조
◦
입력: 사진 한 장 (하나의 입력)
◦
출력: 사진에 대한 설명 (여러 단어들로 구성된 문장)
◦
추가 예시 : 이미지에 대한 설명 생성, 오디오 파일로부터 자막 생성
•
Many-to-One (감성 분석)
◦
여러 개의 입력을 받아 하나의 출력을 생성하는 구조
◦
입력: 여러 단어들로 이루어진 문장
◦
출력: 감성 점수 (긍정 또는 부정 등)
◦
추가 예시 : 감정 분석, 문서의 요약, 음악의 장르 분류
•
Many-to-Many (번역)
◦
여러 개의 입력을 받아 여러 개의 출력을 생성하는 구조
◦
입력: 단어들로 이루어진 문장 (원문)
◦
출력: 단어들로 이루어진 문장 (번역된 문장)
◦
추가 예시 : 순차적인 데이터인 경우 사용 - 두 언어 간의 변환, 대화 시스템에서 문맥에 맞는 응답 생성, 비디오 프레임 분석 등
순차적 데이터 : 순서에 따라 연속적으로 이어지는 데이터 텍스트 데이터, 시계열 데이터, 음성 데이터, 동영상 프레임 등

연산

•
기본 구조
•
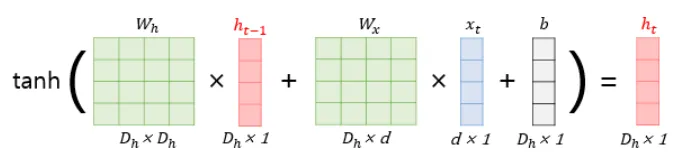
현재 시점 t에서의 은닉 상태값을 hth_t라고 정의. 은닉층의 메모리 셀은 hth_t를 계산하기 위해서 총 두 개의 가중치를 가진다.
•
하나는 입력층을 위한 가중치 WxW_x이고, 하나는 이전 시점 t−1t-1의 은닉 상태값인 ht−1h_{t-1}을 위한 가중치 WhW_h이다.
이를 식으로 표현하면 다음과 같다.
◦
은닉층: ht=tanh(Wxxt+Whht−1+b)h_t = tanh(W_x x_t + W_h h_{t-1} + b)
◦
출력층: yt=f(Wyht+b)y_t = f(W_y h_t +b)
▪
f()f()는 activatefunctionactivate function