.gif&blockId=11b00c82-b138-8050-a58b-dcbceda2ef8f)
DP란?
•
기본적인 아이디어로 하나의 큰 문제를 여러 개의 작은 문제로 나누어서 그 결과를 저장하여 다시 큰 문제를 해결할 때 사용하는 것
•
큰 문제를 작은 문제로 쪼개서 그 답을 저장해두고 재활용한다.
DP가 나온 이유는 무엇일까?
•
완전 탐색, DFS, BFS와 같이 수 많은 경우의 수를 전부 따져봐야 하는 알고리즘 문제에서 해당 경우의 수가 너무 많을 때 속도가 느려지는 문제에서 수행 시간을 개선하고자 나온 알고리즘이다.
•
DP를 사용하지 않았을 때는 최단 경로를 찾거나 최고 점수를 만들어야 하는 문제에선 결국 모든 조합을 다 따져봐야했다.
•
그래서 DP를 사용하여 모든 조합을 찾지 않아도 중복되는 부분을 줄여서 찾아 수행 시간을 단축시키려고 나왔다.
DP의 사용 조건
1.
Overlapping Subproblems(겹치는 부분 문제)
•
DP는 기본적으로 문제를 나누고 그 문제의 결과 값을 재활용해서 전체 답을 구한다.
•
그래서 동일한 작은 문제들이 반복하여 나타나는 경우에 사용이 가능하다.
•
부분 문제가 반복적으로 나타나지 않는다면 재사용이 불가능하니 부분 문제가 중복되지 않는 경우에는 사용할 수 없다.
2.
Optimal Substructure(최적 부분 구조)
•
부분 문제의 최적 결과 값을 사용해 전체 문제의 최적 결과를 낼 수 있는 경우
•
특정 문제의 정답은 문제의 크기에 상관없이 항상 동일하다.
•
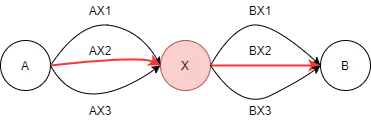
ex) A - B까지의 가장 짧은 경로를 찾고자 하는 경우, 중간에 X가 있을 때, A - X / X - B가 많은 경로 중 가장 짧은 경로라면 전체 최적 경로도 A - X - B가 정답이 된다.
◦
이 때 전체 최단 경로는 변하지 않는다.
•
위 그림처럼 부분 문제에서 구한 최적의 결과가 전체 문제에서도 동일하게 적용되어 겨로가가 변하지 않을 때 사용이 가능하다.
DP를 이해해보자.
문제 : DP를 사용하지 않았을 때
프로그래머스 - 정수 삼각형
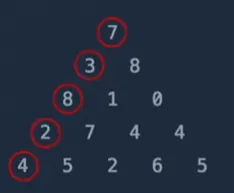
삼각형의 꼭댓기에서 바닥까지 이어지는 경로 중, 거쳐간 숫자의 최댓값을 리턴하는 문제
SUM : 24
SUM : 25 → MAX : 24
SUM : 30 → MAX : 25
•
위와 같이 최댓값을 찾기 위해서 BFS를 사용할 경우 모든 경우의 수를 다 따져가면서 문제를 풀어야 한다.
•
이 때 그림처럼 5줄 짜리 삼각형이면 DFS로 푸는데 지장은 없지만 500줄 5000줄이 될 경우 수행 시간이 굉장히 길어지게 된다.
•
위 그림에서도 보이듯 7-3-8이라는 중복된 경로가 존재한다.
•
DP는 이런 중복된 경로를 저장시켜놓고 꺼내 쓰는게 핵심이다.
예제
1. 배열 만들기
•
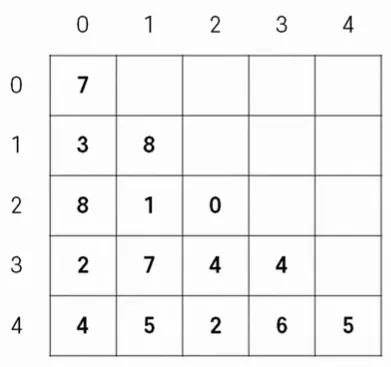
원본 삼각형
문제에 주어진 값을 보유한 배열
•
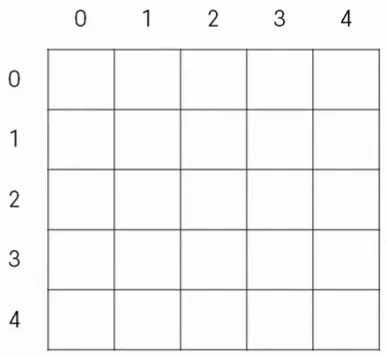
DP 삼각형
해당 위치까지 올 수 있는 최댓값을 저장하는 배열
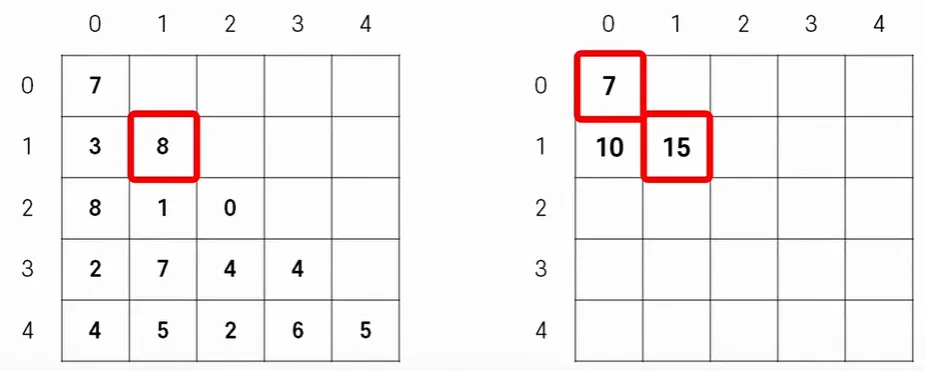
2. 1행 채우기 (0번 줄에서 1번 줄로 내려가는 최댓값)
1.
처음 최댓값은 (0, 0) 자기 자신인 7이다.
2.
(0, 0)에서 내려갈 수 있는 길은 (1, 0)과 (1, 1) 두 가지이다.
3.
(1, 0)까지 올 수 있는 최댓값은 현재 최댓값 (0, 0)인 7에 (1, 0)의 3을 더한 10이다.
4.
(1, 1)까지 올 수 있는 최댓값은 현재 최댓값 (0, 0)인 7에 (1, 1)의 8을 더한 15이다.
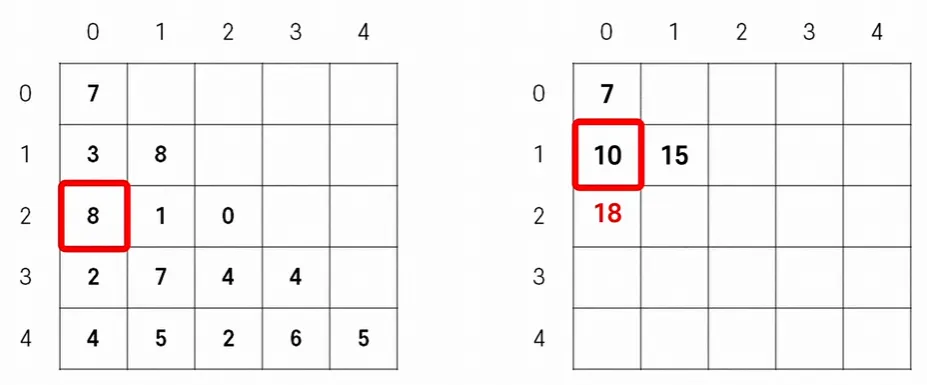
3. 2행 채우기 (1번 줄에서 2번 줄로 내려가는 최댓값)
1.
(2,0)
a.
(1, 0)의 값인 10에 (2, 0)의 값인 8을 더하면 18이라는 값이 (2,0)에 담기게 된다.
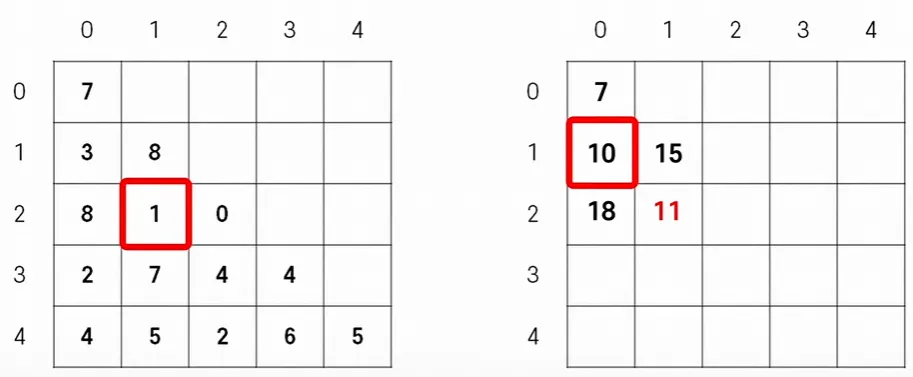
2.
(2, 1)
a.
(1, 0)의 값인 10에 (2, 1)의 값인 1을 더하면 11이라는 값이 (2,1)에 담기게 된다.
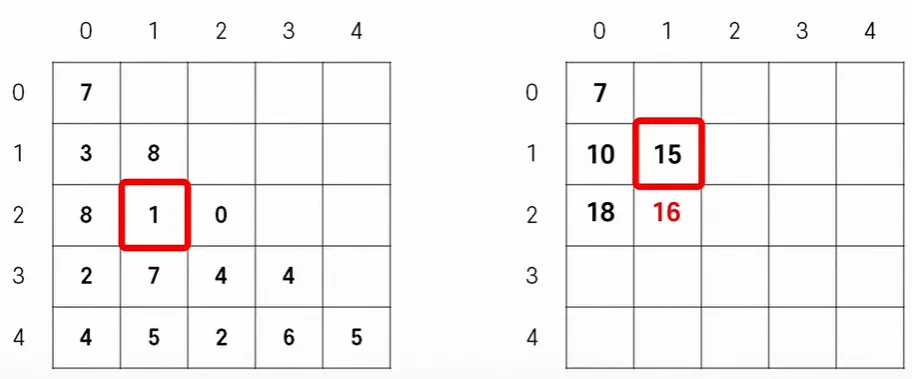
b.
(1, 1)의 값인 15에 (2, 1)의 값인 1을 더하면 16이 되므로 기존 11보다 크기 때문에 최댓값을 갱신한다.
•
동작의 의미 파악
◦
기존 7+3+1 조합과 새로운 7+8+1 조합을 비교하여 진짜 최댓값인 16으로 갱신시켜준 것
◦
그렇기 때문에 (2, 1)에서 다시 연산을 시작할 때는 7+3+1 조합의 연산은 모두 무시하고 7+8+1 조합만 고려하게 된다.
DFS에서는 7+3+1이라는 조합을 전부 추가적으로 수행해서 수행 속도가 느리겠지만 DP에서는 7+3+1 조합의 연산은 모두 무시하고 7+8+1 조합만 사용하기 떄문에 수행 속도가 더 빨라진다.
DP 정리
1.
메모리를 사용해서 중복 연산을 줄인다.
메모리를 사용한다는 것 = 배열 혹은 자료구조를 만드는 것
2.
중복 연산을 줄여서 수행 속도를 개선한다.
중복 연산을 줄인다 = 연산한 결과를 배열에 담는다.
다이나믹 프로그래밍 문제 알아보고 구분하기
1. DFS/BFS로 풀 수는 있지만 경우의 수가 너무 많은 문제
a.
조합 유추하기.
•
예시 문제에선 1줄, 2줄, 3줄, 4줄일 때의 조합을 유추할 수 있다.
b.
패턴을 찾아라.
•
위 예시의 조합을 보고 1부터 시작해서 2배씩 증가하는 패턴임을 알 수 있다.
c.
수학적으로 정리해보자.
•
패턴을 보면 식이 나오는데 이걸 통해서 경우의 수가 얼마나 되는지, 어떻게 로직을 세워야 하는지를 알 수 있다.
d.
경우의 수를 따져봐라.
•
만약 문제에서 n(줄/행)이 500이라고 주어졌을 때 경우의 수 최댓값은 가 나오는 것을 알 수 있고 이는 이 나오게 된다.
•
BFS, DFS로 풀 수 있는 최악의 수 마지노선은 500만개인데 이는 수학식으로 이다.
•
그렇다면 위 문제에선 절대 못푼다는 소리가 나오게 된다.
e.
이제 DP를 고민해보자.
2. 경우의 수들에 중복적인 연산이 많은 경우
•
어차피 안될 조합은 버리고 챙길 조합만 챙기자
공부법
•
그냥 문제를 많이 풀어보자.
•
경험이 축적되야 터득이 빨라진다.
•
30분 정도 고민해보고 정 안 되겠다 싶으면 그냥 풀이를 보고 구현해보는 쪽으로 하자.
