Model Layers and Auto Defferentiation

대분류

인공지능/데이터

소분류

ML/DL 정리 노트

유형

딥 러닝

부유형

Introduction Pytorch

최종 편집 일시

2024/10/27 15:18

생성 일시

2024/10/17 00:20

14 more properties

What is a neural network

Components of a neural network

Build a neural network

1. 훈련에 사용될 하드웨어 디바이스 선택

Automatic differentiation(자동미분)

Forward Propagation(순전파)

Backward Propagation(역전파)

Tensors, Functions and Computational graph

Computing gradients

Disabling gradient tracking

What is a neural network

•

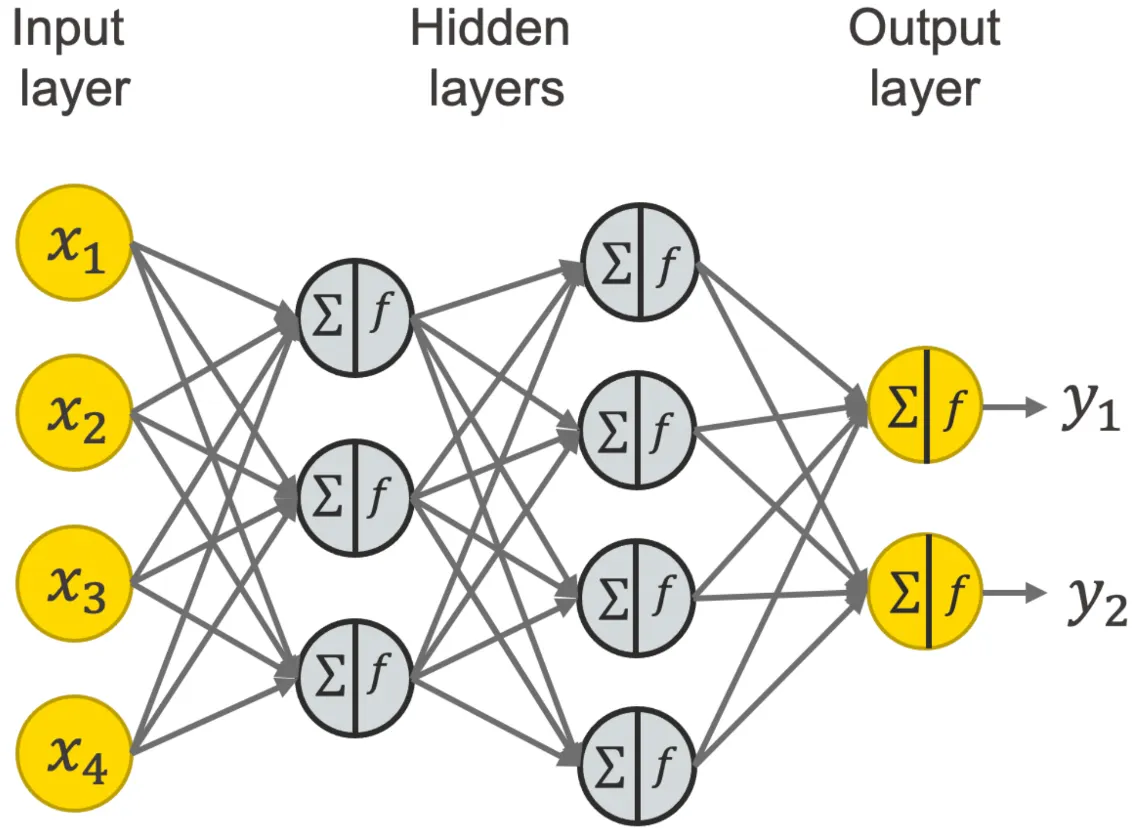
첫번째 Hidden layer

y = f(b + w_1x_1 + w_2x_2 + w_3x_3 + w_4x_4)

•

두번째 Hidden layer

y = f(b + w_1x_1 + w_2x_2 + w_3x_3)

Components of a neural network

•

weight(가중치) = 네트워크의 출력이 예상 출력 값에 얼마나 근접하는지에 영향

•

bias(편향) = 활성화 함수의 출력과 의도한 출력 간의 차이]

y = f(w_1x_1 + w_2x_2 + b)

y = f(\sum{w_ix_i}+b)

Build a neural network

%matplotlib inline
# 리눅스/윈도우 등과 같은 os를 사용할 수 있게 도와주는 모듈
import os

# deep learning 모델을 생성/학습/추론 등을 도와주는 모듈
import torch
# nn -> neural network -> 딥러닝 모델
from torch import nn
# torch의 DataLoader -> 딥러닝 모델이 학습을 할 수 있도록 데이터를 배치 크기 단위로 제공하는 모듈
from torch.utils.data import DataLoader
# datasets -> 학습용 데이터를 딥러닝 모델이 이해할 수 있도록 torch로 형변환하는 모듈
# transforms -> features 데이터를 전처리 해주는 모듈
from torchvision import datasets, transforms
Python
복사

1. 훈련에 사용될 하드웨어 디바이스 선택

device = 'cuda' if torch.cuda.is_available() else 'cpu'
print(f'Using {device} device')
Python
복사

2. nn.Module 클래스 정의

# 딥러닝 모델을 만들려면, nn.Module을 상속 받아야 함!!!
# -> 생성함수(__init__)
#    -> 학습함수에서 사용할 변수를 선언
# -> 학습함수(forward)
#    -> input으로 features 받아야 함!!
class NeuralNetwork(nn.Module):
    # 생성함수 -> 자식 클래스를 인스턴스화
    def __init__(self):
        # super() 부모 클래스 -> nn.Module
        # super().__init__() -> 부모 클래스를 인스턴스화
        super().__init__() # super(NeuralNetwork, self).__init__()
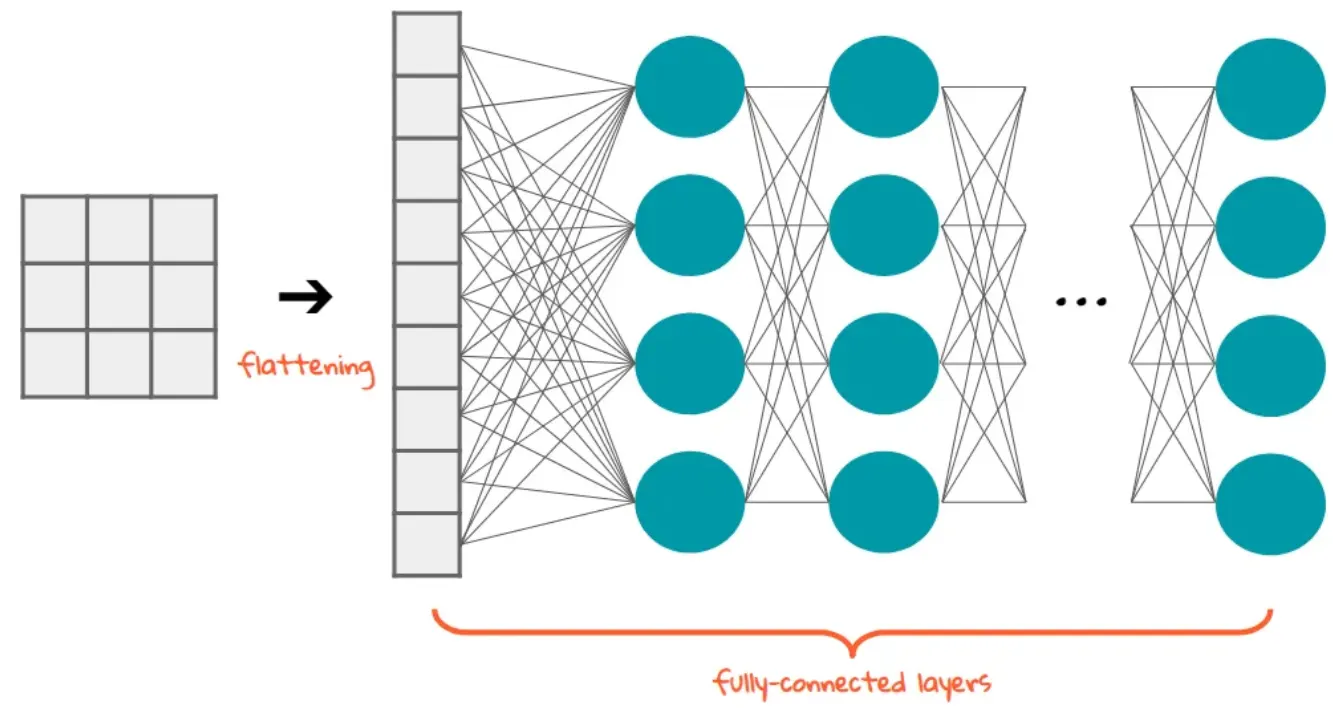
        # nn.Flatten() -> n 차원의 데이터를 vector로 변경해주는 함수
        # -> (28,28) -> (28*28,)
        self.flatten = nn.Flatten()
        # nn.Sequential -> 안에 있는 레이어를 순서대로 실행해주는 함수
        self.linear_relu_stack = nn.Sequential(
            # nn.Linear(input_size, output_size) -> 선형 모델

            # 첫번째 레이어의 input_size는 features_size와 같다!
            # -> 28*28 크기를 갖는 feature만 학습이 가능
            nn.Linear(28*28, 512),
            # nn.ReLU() -> 활성화 함수(선현 모델을 비선형 모델로 변경해주는 역할)
            nn.ReLU(),

            # 두번째 레이어의 input_size는 첫번째 레이어의 output_size와 같다.
            nn.Linear(512, 512),
            nn.ReLU(),

            # 세번째 레이어의 output_size는 target_size와 같다.
            # -> target_size는 10
            # 세번째 레이어의 input_size는 두번째 레이어의 output_size와 같다.
            nn.Linear(512, 10),
            nn.ReLU()
        )

    def forward(self, x): # (batch_size, 28, 28)
        print("학습 시작했어요 ^^")
        out_flatten = self.flatten(x) # out_flatten: (batch_size, 28*28)
        logits = self.linear_relu_stack(out_flatten) # logits: (batch_size, 10)
        return logits
Python
복사

•

NeuralNetwork를 만들고 device에 적용

model = NeuralNetwork().to(device) # 하드웨어에 모델 저장
print(model)
Python
복사

NeuralNetwork(
  (flatten): Flatten(start_dim=1, end_dim=-1)
  (linear_relu_stack): Sequential(
    (0): Linear(in_features=784, out_features=512, bias=True)
    (1): ReLU()
    (2): Linear(in_features=512, out_features=512, bias=True)
    (3): ReLU()
    (4): Linear(in_features=512, out_features=10, bias=True)
    (5): ReLU()
  )
)
Python
복사

4.Model layers

# (batch_size, features1, features2)
input_image = torch.rand(3, 28, 28)
print(input_image.size())
Python
복사

nn.Flatten

# flatten 생성
flatten = nn.Flatten()

flat_image = flatten(input_image) # (3, 28, 28)
print(flat_image.size()) # (3, 28 * 28)
Python
복사

nn.Linear

# linear 생성
layer1 = nn.Linear(in_features=28*28, out_features=20)

hidden1 = layer1(flat_image) # flat_image -> (3, 28 * 28)
print(hidden1.size()) # hidden1 -> (3, 20)
Python
복사

nn.ReLU

•

Linear output: x = weight * input + bias

•

ReLU: f(x) = 0 if x < 0 else x

print(f"Before ReLU: {hidden1}\n\n")
hidden1 = nn.ReLU()(hidden1)
print(f"After ReLU: {hidden1}")

Before ReLU: tensor([[ 0.2826, -0.4782, -0.0358, -0.6311,  0.4889, -0.1665,  0.4779, -0.1052,
          0.1502,  0.0660,  0.3299,  0.6115, -0.2084,  0.5777,  0.0515,  0.0722,
          0.6335,  0.0632,  0.4001, -0.4047],
        [ 0.3017, -0.1036, -0.2424, -0.7319,  0.1596,  0.1269,  0.4524, -0.1588,
          0.0712, -0.0481,  0.3125,  0.6833, -0.2455,  0.7615,  0.1625, -0.0434,
          0.7479,  0.2325,  0.1314, -0.1276],
        [ 0.4567, -0.5776, -0.2184, -0.3951,  0.1225, -0.0140,  0.4541, -0.0516,
         -0.1272, -0.0818,  0.3577,  0.7219, -0.2957,  0.5377,  0.0630, -0.1395,
          0.9187,  0.3089, -0.1543, -0.1834]], grad_fn=<AddmmBackward0>)


After ReLU: tensor([[0.2826, 0.0000, 0.0000, 0.0000, 0.4889, 0.0000, 0.4779, 0.0000, 0.1502,
         0.0660, 0.3299, 0.6115, 0.0000, 0.5777, 0.0515, 0.0722, 0.6335, 0.0632,
         0.4001, 0.0000],
        [0.3017, 0.0000, 0.0000, 0.0000, 0.1596, 0.1269, 0.4524, 0.0000, 0.0712,
         0.0000, 0.3125, 0.6833, 0.0000, 0.7615, 0.1625, 0.0000, 0.7479, 0.2325,
         0.1314, 0.0000],
        [0.4567, 0.0000, 0.0000, 0.0000, 0.1225, 0.0000, 0.4541, 0.0000, 0.0000,
         0.0000, 0.3577, 0.7219, 0.0000, 0.5377, 0.0630, 0.0000, 0.9187, 0.3089,
         0.0000, 0.0000]], grad_fn=<ReluBackward0>)
Python
복사

nn.Sequential

# nn.Sequential -> 안에 있는 레이어를 순서대로 실행
seq_modules = nn.Sequential(
    flatten,
    layer1, # (28*28, 20)
    nn.ReLU(),
    nn.Linear(20, 10)
)

input_image = torch.rand(3,28,28)

logits = seq_modules(input_image)

> logits.shape
torch.Size([3, 10])
Python
복사

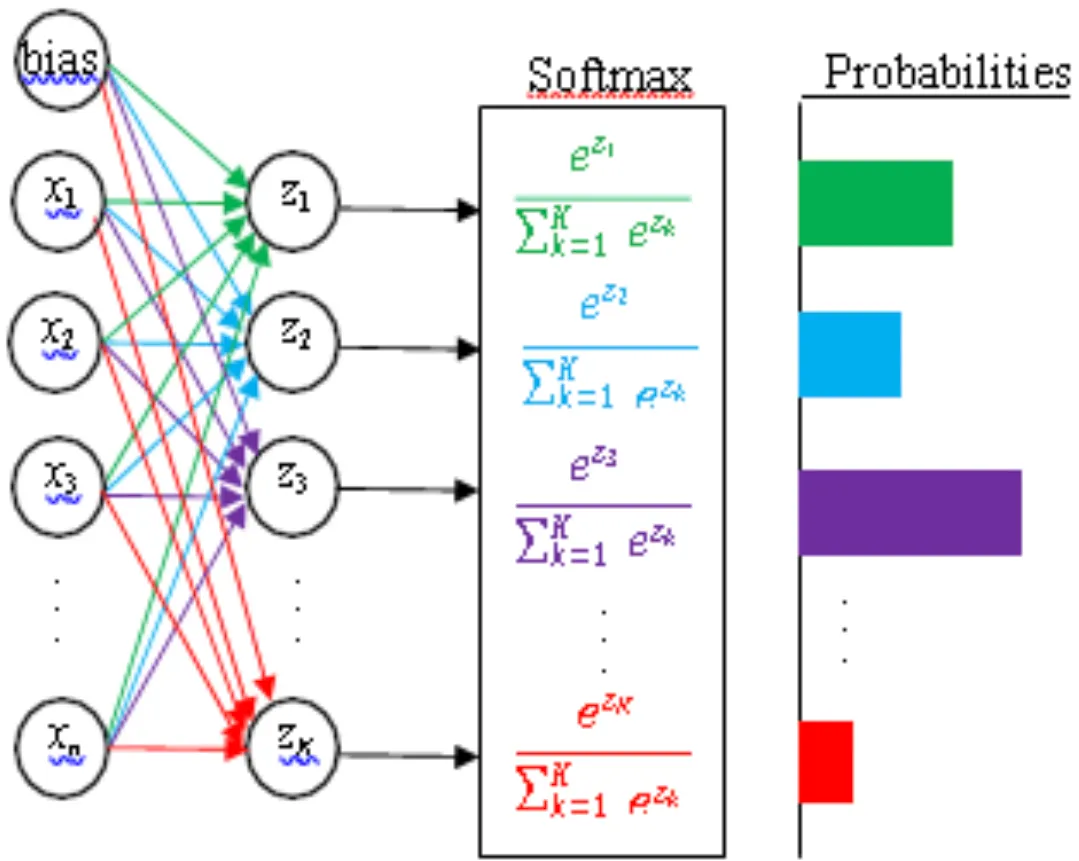
nn.Softmax

softmax = nn.Softmax(dim=1)
pred_probab = softmax(logits)

> pred_probab.shape
torch.Size([3, 10])
Python
복사

5.Model parameters

print("Model structure: ", model, "\n\n")

for i, (name, param) in enumerate(model.named_parameters()):
    print(f"{i}번째, Layer: {name} | Size: {param.size()} | Values : {param[:2]} \n")
Python
복사

Model structure:  NeuralNetwork(
  (flatten): Flatten(start_dim=1, end_dim=-1)
  (linear_relu_stack): Sequential(
    (0): Linear(in_features=784, out_features=512, bias=True)
    (1): ReLU()
    (2): Linear(in_features=512, out_features=512, bias=True)
    (3): ReLU()
    (4): Linear(in_features=512, out_features=10, bias=True)
    (5): ReLU()
  )
) 


0번째, Layer: linear_relu_stack.0.weight | Size: torch.Size([512, 784]) | Values : tensor([[ 0.0051, -0.0264,  0.0349,  ..., -0.0113, -0.0163,  0.0005],
        [-0.0279, -0.0011, -0.0182,  ..., -0.0355, -0.0305, -0.0042]],
       grad_fn=<SliceBackward0>) 

1번째, Layer: linear_relu_stack.0.bias | Size: torch.Size([512]) | Values : tensor([ 0.0289, -0.0258], grad_fn=<SliceBackward0>) 

2번째, Layer: linear_relu_stack.2.weight | Size: torch.Size([512, 512]) | Values : tensor([[-0.0179, -0.0038, -0.0322,  ..., -0.0206, -0.0286, -0.0135],
        [ 0.0012, -0.0280, -0.0273,  ..., -0.0417,  0.0397,  0.0163]],
       grad_fn=<SliceBackward0>) 

3번째, Layer: linear_relu_stack.2.bias | Size: torch.Size([512]) | Values : tensor([-0.0415,  0.0110], grad_fn=<SliceBackward0>) 

4번째, Layer: linear_relu_stack.4.weight | Size: torch.Size([10, 512]) | Values : tensor([[-0.0071,  0.0086,  0.0301,  ...,  0.0281, -0.0350,  0.0328],
        [ 0.0209, -0.0027, -0.0258,  ..., -0.0195, -0.0110,  0.0344]],
       grad_fn=<SliceBackward0>) 

5번째, Layer: linear_relu_stack.4.bias | Size: torch.Size([10]) | Values : tensor([0.0156, 0.0235], grad_fn=<SliceBackward0>) 
Python
복사

Automatic differentiation(자동미분)

•

Gradient Descent를 이용해 손실함수의 최솟값을 쫓아가면서 가중치들을 업데이트하는 것

•

Automatic differentiation은 Forward Propagation(순전파) -> Backward Propagation(역전파) 순서로 진행된다.

Forward Propagation(순전파)

•

신경망은 정답을 맞추기 위해 최선의 추측을 한다.

•

이렇게 추측을 하기 위해서 입력 데이터를 각 함수들에서 실행한다.

Backward Propagation(역전파)

•

신경망은 추측한 값에서 발생한 오류에 비례하여 매개변수들을 적절히 조절한다.

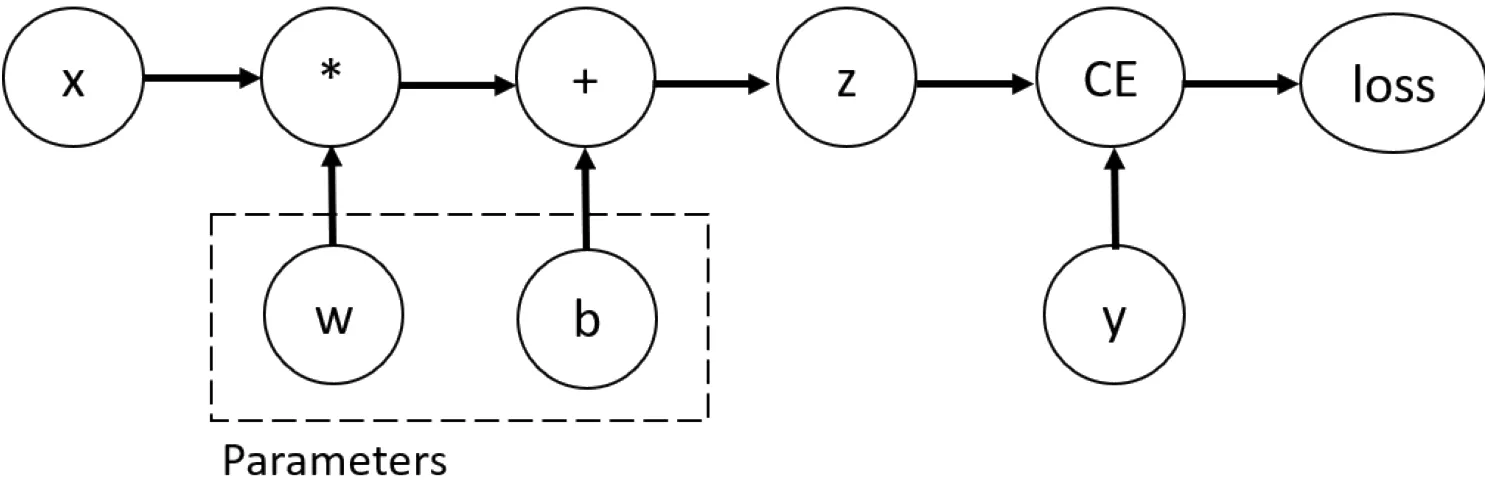
Tensors, Functions and Computational graph

•

z: prediction(예측값)

•

x: features(피처)

•

y: target(타겟)

•

CE: loss function(손실 함수)

◦

target과 prediction 차이를 숫자로 표현하는 함수

z = b + wx

loss = ce(z, y)

Computing gradients

loss.backward()

print(w.grad)
print(b.grad)
Python
복사

tensor([[0.3202, 0.0967, 0.0895],
        [0.3202, 0.0967, 0.0895],
        [0.3202, 0.0967, 0.0895],
        [0.3202, 0.0967, 0.0895],
        [0.3202, 0.0967, 0.0895]])
tensor([0.3202, 0.0967, 0.0895])
Python
복사

Disabling gradient tracking

z = torch.matmul(x, w)+b
> print(z.requires_grad)
True

with torch.no_grad(): # No gradient tracking(테스트용)
    z = torch.matmul(x, w)+b
> print(z.requires_grad)
False
Python
복사

•

다른 방법 : 텐서에서 detach() 메소드 사용하기

z = torch.matmul(x, w)+b
z_det = z.detach() # No gradient tracking(테스트용)
print(z_det.requires_grad)
Python
복사