.gif&blockId=11b00c82-b138-8050-a58b-dcbceda2ef8f)
•
“부동”이라는 한자는 떠다니며 정해진 위치가 없음을 의미
•
이는 “float”라는 영어 단어와 깊은 연관이 있다.
•
컴퓨팅에서 “float”는 부동소수점 수를 지칭하는데, 이 용어는 소수점의 위치가 고정되어 있지 않고 데이터의 크기나 정밀도에 따라 자유롭게 이동할 수 있다는 사실을 반영한다.
•
이러한 특성은 컴퓨터가 다양한 범위의 실수를 효율적으로 표현할 수 있게 해준다.
고정소수점
•
고정소수점 방식에서는 숫자를 정수 부분과 소수 부분으로 나누어 각각 고정된 위치에 저장한다.
•
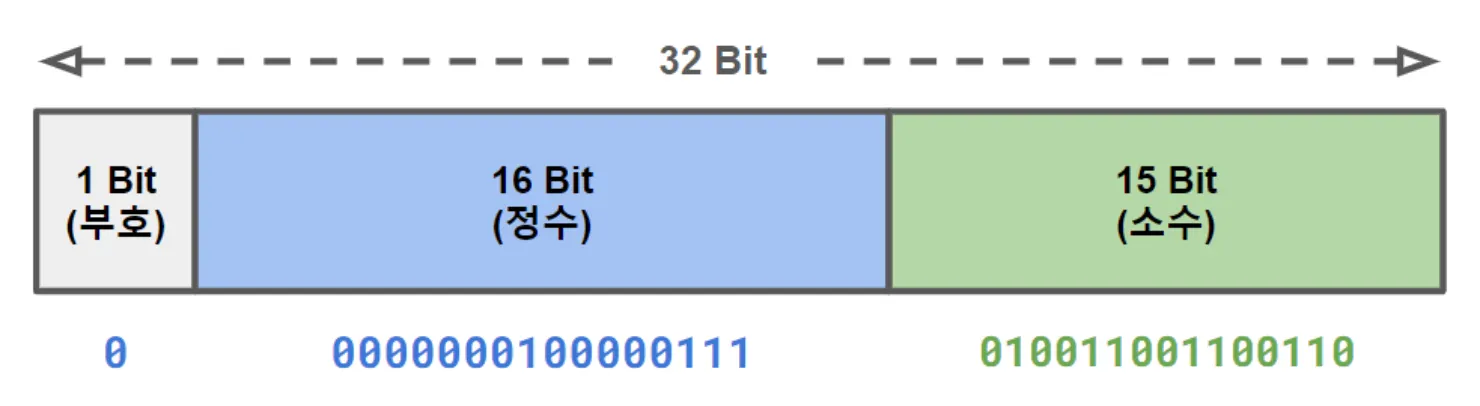
예를 들어, 263.3이라는 숫자를 4바이트(32비트) 시스템에서 표현한다고 가정하였을 때, 여기서 부호는 1비트, 정수 부분은 16비트, 소수 부분은 15비트를 사용한다고 한다.
•
정수 부분(263): 2진수로 변환하면 0000000100000111이다.
•
소수 부분(0.3): 2진수로 근사치를 표현하면 010011001100110이다. (정확한 표현은 불가능하므로 근사치 사용).
→ 따라서, 이 시스템에서 263.3은 부호 비트가 0(양수), 정수 부분이 0000000100000111, 소수 부분이 010011001100110으로 표현된다.
부동소수점
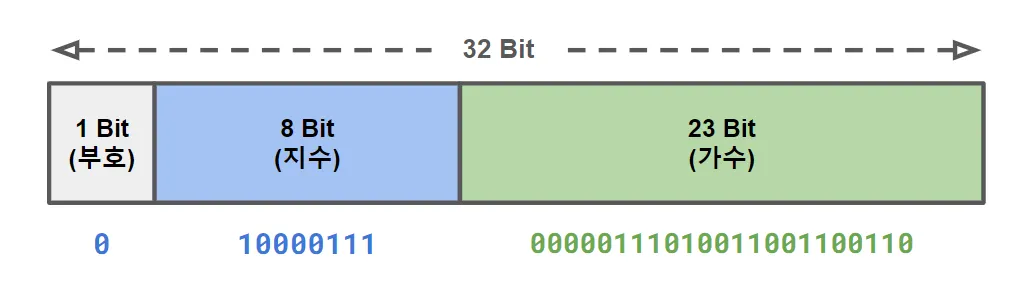
부동소수점 수는 가수(mantissa)와 지수(exponent)로 구분하여 표현
•
부호(bit): 양수이므로 0이다.
•
정규화: 263.3 을 2진수로 변환하면 100000111.01001100110011001100110011...(무한반복)이고, 정규화를 통해 1.0000011101001100110011001100110011... * 2^8로 표현할 수 있다.
•
가수(mantissa): 소수점 이하 부분을 사용
필요하다면 23비트로 맞추기 위해 뒷부분을 잘라내거나 0으로 채운다.
•
지수(exponent)와 Bias: 지수는 8이고, IEEE 754 표준에서는 32비트 부동소수점의 경우 지수에 127(Bias)를 더한 값을 사용한다.
따라서, 지수 부분은 8 + 127 = 135, 2진수로 10000111이다.
•
이런 식으로, 263.3은 부동소수점으로 표현될 때 부호, 지수, 가수 부분을 각각 0, 10000111, 00000111010011001100110으로 나타낼 수 있다.
부동소수점에서 편향(Bias) 127을 더하는 이유
•
지수 표현의 범위를 조정하기 위해서
•
지수를 부호 없는 정수로 표현할 때, 음수 지수와 양수 지수를 모두 다루어야 한다.
•
하지만 부동소수점 표준에서는 음수를 다루는 대신 Bias 값을 더하여 모든 지수를 양수로 만들어 처리한다.
•
이렇게 함으로써 지수를 부호 없는 정수로 표현할 수 있으며, 지수의 범위를 더 크게 확보할 수 있다.
