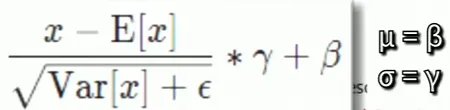Batch Normalization

대분류

인공지능/데이터

소분류

ML/DL 정리 노트

유형

딥 러닝

부유형

기초

주요 레퍼런스

https://www.youtube.com/watch?v=LpXeOt3xmhM&list=LL&index=1

https://only-wanna.tistory.com/entry/Affine-%EB%B3%80%ED%99%98%EA%B3%BC-%EB%94%A5%EB%9F%AC%EB%8B%9D

최종 편집 일시

2024/11/15 08:08

생성 일시

2024/11/12 14:00

13 more properties

배치 정규화(Batch Normalization)

Batch Normalization의 필요성

Covariate Shift

Covariate Shift 해결책 ⇒ Batch Normalization

running mean(이동 평균)과 running variance(이동 분산)

개념

Running Mean과 Running Variance가 필요한 이유

계산 방식

학습과 추론에서의 활용

Batch Normalization의 작동 원리

배치 정규화(Batch Normalization)

•

모델 학습 과정에서 신경망의 각 레이어 입력 데이터 분포를 정규화(normalization)하여 학습 속도를 향상시키고, 과적합(overfitting)을 줄이는 역할을 하는 중요한 기법

Batch Normalization의 필요성

•

딥러닝 모델의 여러 층을 학습할 때, 각 층의 입력 분포가 계속해서 변할 수 있다. 

•

이를 내부 공변량 변화(Covariate Shift)라고 하며, 이는 모델 학습을 불안정하게 만들고, 더 많은 학습 에포크를 요구한다.

•

Batch Normalization은 이 문제를 해결하기 위해 각 미니배치(mini-batch) 단위로 데이터의 분포를 정규화하여 입력 분포의 변화를 억제하고 모델의 학습을 안정화한다.

Covariate Shift

•

모델이 훈련할 때 사용한 데이터와 실제 테스트할 때의 데이터가 서로 다른 분포를 가지는 문제

◦

나중 모듈 입장에서는 최선을 다하고 있지만 주어진 입력의 특성이 계속 달라져 학습이 비교적 불안정하게 진행된다.

•

입력 변수의 분포 P(X)P(X)P(X)가 훈련과 테스트(또는 실제 환경) 간에 달라지지만, 출력 변수 YYY 조건부 분포 P(Y∣X)P(Y∣X)P(Y∣X)는 일정하게 유지되는 상황

→ 학습 데이터에서의 입력 분포

P_{train}(X)

와 실제 데이터(테스트 데이터)의 입력 분포

P_{test}(X)

가 서로 다르지만, 조건부 분포

P(Y|X)

는 동일하다.

Covariate Shift 해결책 ⇒ Batch Normalization

•

위 Covariate Shift를 완화시켜주는 대책으로 나온 것이 정규화.

•

정규화를 하게 되면 입력 숫자 특성이 거의 일정해진다.

\frac{x-E[x]}{\sqrt{Var[x]+\epsilon}} * \gamma + \beta

◦

각 학습 Iteration 때마다 채널 각각에 대해서 평균(μ) 0, 표준편차(σσσ) 1이 되고 가중치(weight, γ \gammaγ)를 곱하고 편향(bias, β\betaβ)을 더하면 평균 bias에 표준편차 weight가 된다.

\mu = \beta \\ \sigma = \gamma

◦

여기서 weight랑 bias는 업데이트가 조금씩 되기 때문에 나중 모듈(fc2)입장에서는 흔들린 입력(γ+β\gamma+\betaγ+β)이긴 하지만 그 두 개의 의해서만 값이 바뀌기 때문에 선형적으로 흔들리는 것에 가깝다.

◦

Affine변환으로 흔들림

Affine변환 : 직선과 평형성을 그대로 유지하는 변환
Linear Transformation에 Traslation 항이 추가된 형태

towardsdatascience

◦

결론적으로 나중 모듈(fc2)입장에서는 덜 흔들리는 입력의 변화라고 할 수 있다.

running mean(이동 평균)과 running variance(이동 분산)

개념

•

Running Mean: 학습 과정에서 미니배치 단위로 계산된 평균을 누적하여 이동 평균 형태로 저장해둔 값.

•

Running Variance: 학습 과정에서 미니배치 단위로 계산된 분산을 누적하여 이동 분산 형태로 저장해둔 값.

Running Mean과 Running Variance가 필요한 이유

•

학습 시에는 미니배치의 평균과 분산을 사용하여 정규화를 수행하지만, 추론 시에는 배치 크기(batch size)가 1인 경우도 많고, 고정된 평균과 분산을 사용하는 것이 일반적으로 더 안정적이다.

•

학습 시 매 미니배치마다 계산되는 평균과 분산은 추정치이므로 다소 불안정할 수 있다. 

•

따라서, 학습 동안 전체 데이터셋을 대표할 수 있는 평균과 분산 값을 지속적으로 업데이트하면서 "고정된 값"으로 만들 필요가 있다. 

•

이 고정된 값이 추론 시 사용되며, 이를 running mean과 running variance라고 한다.

계산 방식

•

Running Mean과 Running Variance는 지수 이동 평균(exponentially moving average) 방식을 사용해 업데이트된다.

•

이는 이전의 running 값에 새로운 미니배치의 평균과 분산을 가중합하여 누적하는 방식이다.

•

Running Mean 업데이트

\text{running\_mean} = \text{momentum} \times \text{running\_mean} + (1 - \text{momentum}) \times \text{batch\_mean}

•

Running Variance 업데이트

\text{running\_variance} = \text{momentum} \times \text{running\_variance} + (1 - \text{momentum}) \times \text{batch\_variance}

•

수식 설명

◦

momentum: 이전 running 값과 새로운 배치 값 간의 가중치를 조절하는 하이퍼파라미터

▪

일반적으로 0.9 정도의 값을 사용하며, 이는 이전 값의 영향을 90% 반영하고, 현재 미니배치 값의 영향을 10% 반영하는 것을 의미

◦

batch_mean과 batch_variance: 현재 미니배치에서 계산된 평균과 분산 값

학습과 추론에서의 활용

•

학습 시: 미니배치의 평균과 분산을 사용해 정규화하는 동시에, running mean과 running variance를 업데이트하여 점진적으로 학습 데이터 전체의 평균과 분산을 대표할 수 있는 값으로 수렴하게 만든다.

•

추론 시: 더 이상 미니배치 평균과 분산을 계산하지 않고, 학습 시에 구해둔 running mean과 running variance 값을 사용해 정규화한다. 이렇게 하면 테스트 단계에서 미니배치 크기와 상관없이 안정적인 결과를 얻을 수 있다.

Batch Normalization의 작동 원리

미니배치 평균과 분산 계산

•

입력 데이터 xxx에 대해 미니배치의 평균 μμμ와 분산 σ2σ^2σ2를 계산한다. 이때 미니배치 단위로 진행하여 효율성을 높인다.

미니배치 평균 계산

\mu = \frac{1}{m} \sum_{i=1}^m x_i

•

xix_ixi​: 미니배치 안의 각 데이터 포인트.

•

mmm: 미니배치에 있는 데이터의 개수.

•

μμμ: 미니배치 안에서 각 데이터 포인트 xix_ixi​ 값의 평균

•

미니배치 내의 데이터들이 어떤 분포를 가지는지 확인하기 위한 중간 과정이다.

•

평균을 빼줌으로써, 데이터의 중심을 0에 맞추게 된다. 

→ 데이터의 중심이 매번 동일하게 유지되며, 이를 통해 학습이 더 안정화될 수 있다.

미니배치 분산 계산

\sigma^2 = \frac{1}{m} \sum_{i=1}^m (x_i - \mu)^2

•

σ2σ^2σ2: 미니배치 안의 데이터가 평균을 기준으로 얼마나 퍼져 있는지를 나타내는 값

•

분산을 이용해 스케일을 조정하게 되면, 모델의 각 층에서 입력 값의 크기가 일정하게 유지되어 학습이 더 안정적이다.

정규화 과정 (Normalize)

•

각 입력 값에서 평균을 빼고 분산으로 나누어 정규화한다.

→ 각 데이터 포인트

x_i

에서 미니배치 평균

μ

을 빼고, 미니배치 분산

\sigma^2

의 제곱근으로 나눠 준다.

\hat{x}_i = \frac{x_i - \mu}{\sqrt{\sigma^2 + \epsilon}}

◦

ϵ\epsilonϵ: 매우 작은 양의 상수로, 분모가 0이 되는 것을 방지한다.

◦

데이터의 분포를 평균이 0이고 분산이 1인 정규분포로 변환하는 과정

→ 평균과 분산을 조정하여 입력 데이터가 항상 동일한 분포를 유지하도록 만들어 준다.

◦

각 층에서 입력 데이터의 분포가 달라지는 문제를 방지하고, 전체 네트워크의 학습을 안정화시킬 수 있다.

스케일링과 시프트 (Scaling and Shifting)

•

학습 가능한 파라미터 γγγ와 β ββ를 사용해 정규화된 값을 다시 스케일링하고 시프트하여 모델이 적합한 분포로 데이터를 변환할 수 있게 한다.

y_i = \gamma \hat{x}_i + \beta

◦

γγγ: 정규화된 데이터를 스케일링하는 학습 가능한 파라미터.

◦

β\betaβ: 정규화된 데이터에 시프트를 주는 학습 가능한 파라미터.

•

이를 통해 단순히 정규화된 분포만 사용하는 대신, 모델이 필요로 하는 분포를 학습할 수 있다.

•

최종 수식

실제 파이썬 코드 구현

import numpy as np

def batch_norm(X, gamma, beta, epsilon=1e-5):
    """
    X: 입력 데이터 (배치 크기 x 특성 크기)
    gamma: 학습 가능한 스케일 파라미터
    beta: 학습 가능한 시프트 파라미터
    epsilon: 안정성을 위한 작은 상수
    """
    # 1. 미니배치 평균과 분산(표준편차) 계산
    mu = np.mean(X, axis=0)
    var = np.var(X, axis=0)
    
    # 2. 정규화
    X_normalized = (X - mu) / np.sqrt(var + epsilon)
    
    # 3. 스케일링과 시프트
    out = gamma * X_normalized + beta
    
    return out
Python
복사

정리하기

학습 파라미터 / 학습 X 파라미터

•

batch normalization은 위에서 설명한 작동 원리에서 나온 것처럼 평균과 분산을 계산한 후 이후 과정에서 두 가지 계산 과정으로 나눌 수 있다.

평균과 분산

•

minibatch단위로 자기 자신에서 평균(μ)과 표준편차/분산(σ2σ^2σ2)를 구한다.

Normalization(정규화)

•

각 입력 값에서 평균을 빼고 분산으로 나누어 정규화한다.

곱셈, 덧셈(Elementwise)

•

채널의 Element 수만큼 가중치(weight - γ\gammaγ)와 편향(bias - β\betaβ)이 있다. 

y_i = \gamma \hat{x}_i + \beta

•

각 채널별 Elementwise로 곱하고 더한다.

고정된 값

•

Normalization(정규화)

•

별도의 파라미터가 들어갈 여지가 없다.

◦

자기 자신에서 평균(μ)과 표준편차/분산(σ2σ^2σ2)를 구한 뒤 빼고 나누기 때문

◦

빼고

◦

나누고

학습 파라미터

•

곱셈, 덧셈(Elementwise)

•

각 채널 별로 곱하고 - 가중치(weight - γ\gammaγ)

•

더한다. - 편향(bias - β\betaβ)

학습 X 파라미터

학습(Training) 때(좌)는 자기 자신 데이터에서 minibatch 기준으로 평균과 분산을 구하는 반면, 추론(Inference) 때(우)는 minibatch라는 개념이 없다.

이 때 추론(Inference) 단계에서 한 번에 여러 추론 요청을 받을 수는 있겠지만 학습에서의 minibatch와는 다른 개념이다.

•

그래서 학습 모드에서는 몰래 Training 데이터셋을 가지고 평균과 분산을 매 Iteration 때마다 계속 계산해 둔다.

•

그리고 그 뒤에 eval모드에서는 minibatch라는 개념이 없기 때문에 학습 때 몰래 계산해둔 평균과 표준편차를 써서 정규화를 한다.

eval(Evaluation)과 Inference의 차이점

구분	Evaluation (Eval)	Inference
목적	모델 성능 평가	실제 예측
설정	드롭아웃 비활성화, Batch Norm의 running mean/variance 사용, minibatch 없음	동일
사용 시점	학습 후 성능 검증, 학습 중 검증	모델 배포 후 실제 환경
출력	성능 지표, 예측 값	예측 값만

요약

	학습 O	학습 X
Train	가중치(weight - $\gamma$ )와 편향(bias - $\beta$ ) - 곱/덧셈	minibatch 축으로 정규화
Eval / Inference	가중치(weight - $\gamma$ )와 편향(bias - $\beta$ ) - 곱/덧셈	평균(μ)과 표준편차/분산( $σ^2$ ) - 정규화

•

곱하고 더하는 파라미터는 학습되는 파라미터이다.

•

빼고 나누는 파라미터(정규화)는 학습이 되지 않는 파라미터/고정된 값이다.