.gif&blockId=11b00c82-b138-8050-a58b-dcbceda2ef8f)
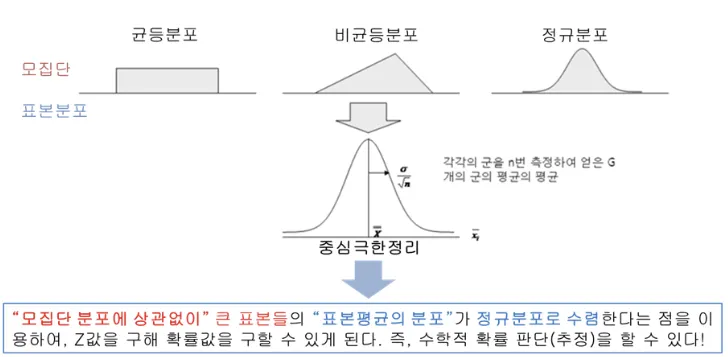
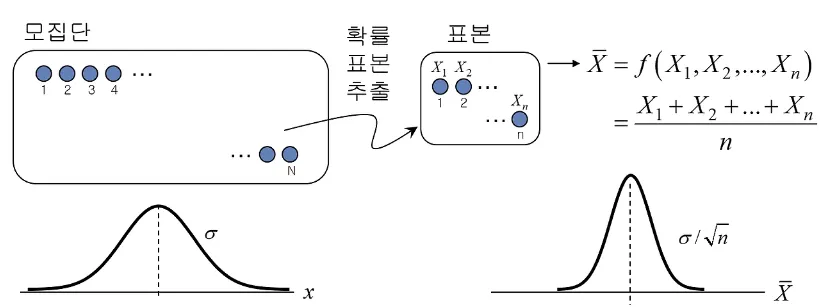
중심극한정리(Central Limit Theorem, CLT)
•
통계학에서 매우 중요한 개념으로, 모집단의 분포와 상관없이 표본 평균의 분포가 큰 표본 크기에서 정규분포에 가까워진다는 내용을 담고 있다.
•
이 정리는 많은 통계적 방법론의 기초를 형성한다.
⇒ 어떤 모집단에서 많은 표본을 뽑아서 그 평균을 구하면 이 평균들이 모여서 만드는 분포는 정규분포(종 모양의 분포)에 가까워진다는 것
모집단이 정규분포일 필요가 없다.
표본을 많이 뽑아 그 평균을 구하면, 그 평균들의 분포는 정규분포처럼 보이게 된다.
중심극한정리의 정의
•
중심극한정리는 다음과 같이 정의된다:
◦
모집단: 평균이 이고 분산이 인 모집단이 있다고 하자.
◦
표본: 이 모집단에서 크기 의 표본을 여러 번 추출하여 각 표본의 평균을 계산한다고 하자.
•
중심극한정리는 다음과 같이 말한다:
◦
표본 크기 이 충분히 크다면, 표본 평균의 분포는 원래 모집단의 분포가 정규분포인지 아닌지에 관계없이 정규분포에 근접하게 된다.
◦
이 정규분포의 평균은 이고, 표준편차(표준오차)는 이다.
•
즉, 표본 평균 는 아래와 같은 분포를 따른다:
중심극한정리의 주요 포인트
1.
모집단의 분포와 무관:
•
모집단이 정규분포든 비정규분포든 관계없이, 표본 평균의 분포는 정규분포에 가까워진다.
2.
표본 크기의 중요성:
•
표본 크기가 커질수록, 표본 평균의 분포는 더욱 정규분포에 가까워진다.
•
일반적으로, 일 때 표본 평균의 분포는 충분히 정규분포에 근접한다고 여겨지지만, 이는 보편적인 기준일 뿐 상황에 따라 다를 수 있다.
3.
표본의 표준오차:
•
표본 평균의 표준편차는 로, 표본 크기가 커질수록 표본 평균의 변동성은 줄어든다.
•
즉, 더 큰 표본 크기에서는 표본 평균이 모집단의 평균에 더 가깝게 집중된다.
예외와 주의사항
•
작은 표본 크기: 표본 크기가 작을 때, 특히 인 경우, 모집단의 분포가 매우 비정규적이면 중심극한정리의 효과가 충분히 발휘되지 않을 수 있다.
•
비대칭 분포: 모집단이 극도로 비대칭적이거나 꼬리가 긴 분포라면, 표본 크기가 매우 커야(예: 또는 더 큼) 정규성을 얻을 수 있다.
