Search

가우시안 정규 분포

대분류
인공지능/데이터
소분류
통계 실험
유형
팁
최종 편집 일시
2024/10/31 05:25
생성 일시
2024/09/08 14:16
15 more properties

가우시안 정규 분포(Gaussian Normal Distribution)

•
통계학에서 가장 중요한 분포 중 하나
•
데이터가 평균을 중심으로 대칭적으로 분포하는 패턴을 설명
•
이는 연속 확률 분포 중 하나이며, 정규 분포(Normal Distribution)라고도 한다.
•
많은 자연현상과 실험 데이터가 정규 분포를 따르는 경향이 있기 때문에, 정규 분포는 실질적인 데이터 분석에서 중요한 역할을 한다.
•
정규 분포의 확률 밀도 함수
f(x)=12πσ2e−(x−μ)22σ2f(x) = \frac{1}{\sqrt{2\pi \sigma^2}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}
◦
μ : 평균(mean)으로, 분포의 중심을 나타낸다.
◦
σ\sigma : 표준 편차(standard deviation)로, 분포의 넓이를 결정. σ2σ^2는 분산(variance)
◦
xx : 확률 변수
◦
ee : 자연로그의 밑, 약 2.718

정규 분포의 특징

•
평균 μ\mu:
◦
정규 분포는 평균 μμ를 중심으로 대칭을 이룬다. 평균은 데이터가 가장 많이 몰려 있는 곳을 나타낸다.
•
표준 편차 σ\sigma
◦
표준 편차 σ는 데이터가 얼마나 흩어져 있는지를 나타내는 지표
◦
값이 클수록 분포가 넓고, 작을수록 분포가 좁다.
•
종 모양 곡선:
◦
정규 분포의 그래프는 종 모양(bell curve)을 가지고 있으며, 대칭적인 형태
•
68-95-99.7 규칙 (Empirical Rule):
◦
정규 분포에서는 평균을 중심으로 값이 다음과 같은 확률을 가집니다:
▪
데이터의 약 68%가 평균 ± 1 표준편차 범위 내에 존재합니다.
▪
데이터의 약 95%가 평균 ± 2 표준편차 범위 내에 존재합니다.
▪
데이터의 약 99.7%가 평균 ± 3 표준편차 범위 내에 존재합니다.

그래프 분석

# Import necessary libraries import numpy as np import matplotlib.pyplot as plt # 평균과 표준편차 설정 mu = 0 sigma1 = 1 sigma2 = 2 # x값 생성 x = np.linspace(-10, 10, 1000) # 가우시안 정규 분포 함수 계산 pdf1 = (1 / (np.sqrt(2 * np.pi * sigma1**2))) * np.exp(- (x - mu)**2 / (2 * sigma1**2)) pdf2 = (1 / (np.sqrt(2 * np.pi * sigma2**2))) * np.exp(- (x - mu)**2 / (2 * sigma2**2)) # 그래프 그리기 plt.figure(figsize=(8, 6)) plt.plot(x, pdf1, label='Standard Deviation 1') plt.plot(x, pdf2, label='Standard Deviation 2') plt.title('Gaussian Normal Distribution') plt.xlabel('x') plt.ylabel('Probability Density') plt.grid(True) plt.legend() plt.show()
Python
복사
•
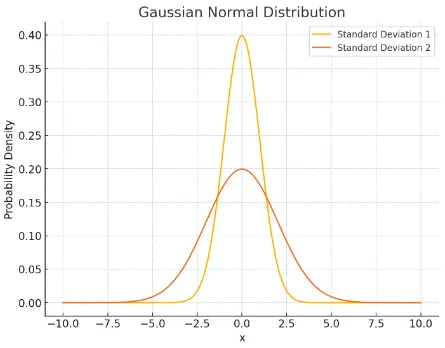
표준 편차 1: 그래프가 좁고 높으며, 분포가 평균에 더 밀집되어 있다.
•
표준 편차 2: 그래프가 넓고 낮으며, 분포가 평균에서 더 멀리 퍼져 있다.
•
이 그래프는 정규 분포가 평균을 중심으로 대칭적으로 분포한다는 것을 보여주며, 표준 편차가 클수록 분포가 넓게 퍼진다.

표준 정규 분포 (Standard Normal Distribution)

•
평균이 0, 표준 편차가 1인 정규 분포
Z=X−μσZ = \frac{X - \mu}{\sigma}
◦
Z : 표준화된 변수
◦
X : 원래의 값
•
분석이나 계산을 간단하게 하기 위해 데이터의 변환에 자주 사용