.gif&blockId=11b00c82-b138-8050-a58b-dcbceda2ef8f)
개요
•
선형대수학 : 벡터, 행렬, 선형변환 등을 연구하는 수학, AI에서 중추적인 역할을 함
•
데이터 표현 : 머신러닝에서 데이터는 일반적으로 행렬이나 벡터의 형태로 표현됨
이미지 데이터 → 픽셀 값들의 행렬
문서 데이터 → 단어들의 벡터
•
선형 변환과 행렬 연산 : 머신러닝에서 모델의 학습과 예측에 사용
•
차원 축소와 특이값 분해 : 데이터의 차원 축소와 관련된 기법 제공
차원 축소 → 고차원 데이터의 특징 추출 및 중요한 정보 유지에 사용
특이값 분해(Singular Value Decomposition, SVD) : 차원 축소와 행렬 분해에 사용
•
최적화 문제와 선형 시스템 : 선형 회귀(Linear Regression)는 최적화 문제로 표현
텐서 용어 정리
스칼라 (Scalar) | 벡터(Vector) | 행렬(Matrix) | 텐서(Tensor) | |
텐서 차원 | 0차원 | 1차원 | 2차원 | 단위 |
설명 | 하나의 값을 가지는 데이터 타입, 크기와 방향의 개념X | 크기와 방향을 모두 가지는 양을 나타내는 개념 | 숫자의 집합을 2차원 배열로 구성한 것, 여러 개의 벡터를 하나의 구조체로 묶어서 표현 가능 | 다차원 배열로 구성된 데이터를 나타내는 개념 |
표현 방식 | 단일 값 | 숫자의 배열로 표현, 행 벡터 또는 열 백터로 나타낼 수 있음. | 행렬은 행(row)과 열(column)로 구성, 각 요소는 행렬의 위치를 나타내는 (i,j)쌍으로 표현 | 2차원까지는 스칼라, 벡터, 행렬
3차원부터는 고차원 텐서 |
예제 | [2],[3] | [5,3,7] | [[4,14,2], [16,4,3]] | 3차원 텐서 : 시계열 데이터, 동영상 데이터
그외 텐서 : 고차원 |
노름(norm): 벡터의 길이
•
벡터의 크기를 나타내는 값
•
L1노름
◦
벡터의 원소의 절댓값을 모두 더한 값
ex) 2차원 벡터 [1, 3]의 L1노름은 |1| + |2| = 3
•
L2노름 (머신러닝에서 주로 사용)
◦
벡터의 원소들의 제곱을 모두 더한 후, 그 값의 제곱근을 취한 것
◦
예제
◦
벡터를 정규화 하는 데에 사용
▪
벡터의 방향은 그대로 유지되면서 크기가 1인 단위 벡터로 변환
→ 모델에서 벡터의 크기에 민감하지 않게 만들 수 있음
◦
벡터 간 거리 측정하는 유클리드 거리(Euclidean distance) 계산 가능
◦
L2 노름 계산법
•
파이토치 예시 파일 (노름 구하기)
import torch
# 벡터 생성
v = torch.tensor([3.0, 4.0])
# L1 노름 구하기
l1_norm = torch.norm(v, p=1)
# L2 노름 구하기
l2_norm = torch.norm(v, p=2)
print("L1 norm:", l1_norm)
print("L2 norm:", l2_norm)
Python
복사
일차독립(선형독립)
•
일차독립(선형독립)
◦
벡터들이 선형적으로 독립적인 상태
◦
하나의 벡터를 다른 벡터의 선형조합으로 나타낼 수 없는 상태
•
벡터 a, b, c의 일차독립
◦
a + 2b + 3c = 0의 일차독립 경우는 a = b = c = 0
◦
위 식을 만족 시키기 위해서 a, b, c 중 하나 이상의 벡터를 다른 벡터들의 선형조합으로 나타낼 수 없기 때문
•
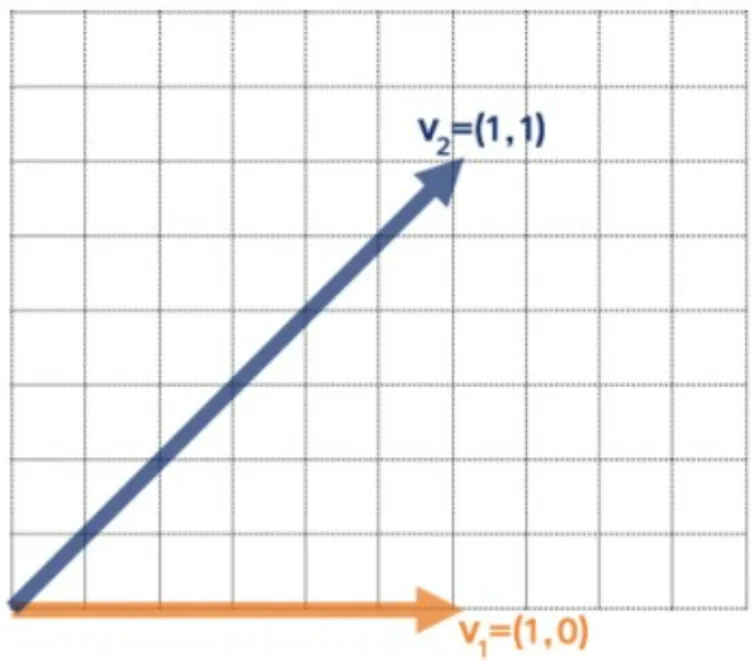
세 벡터 (1,0,0), (0,1,0), (0,0,1)은 일차 독립인가?
◦
c₁(1,0,0) + c₂(0,1,0) + c₃(0,0,1) = (c₁, c₂, c₃)에서
c₁(1,0,0) + c₂(0,1,0) + c₃(0,0,1) = 0 (0벡터) 이면
c₁ = c₂ = c₃ = 0 이므로 주어진 세 벡터는 일차 독립
◦
위 식에서 =0이 되는 값은 스칼라인 c₁, c₂, c₃가 0이 되어야만 가능하기(0이 아닌 다른 해는 존재하지 않음)때문에 일차 독립
일차 종속
•
벡터들이 선형적으로 종속적인 상태
•
0이 아닌 다른 해를 가질 수 있으면 일차 종속
•
하나의 벡터를 다른 벡터들의 선형조합으로 나타낼 수 있는 상태
◦
ex) a + 2b + 3c = 0 일 때, a = -2b - 2c
◦
위 식을 만족시키는 a, b, c의 조합이 존재하기 때문에 a, b, c는 일차종속
•
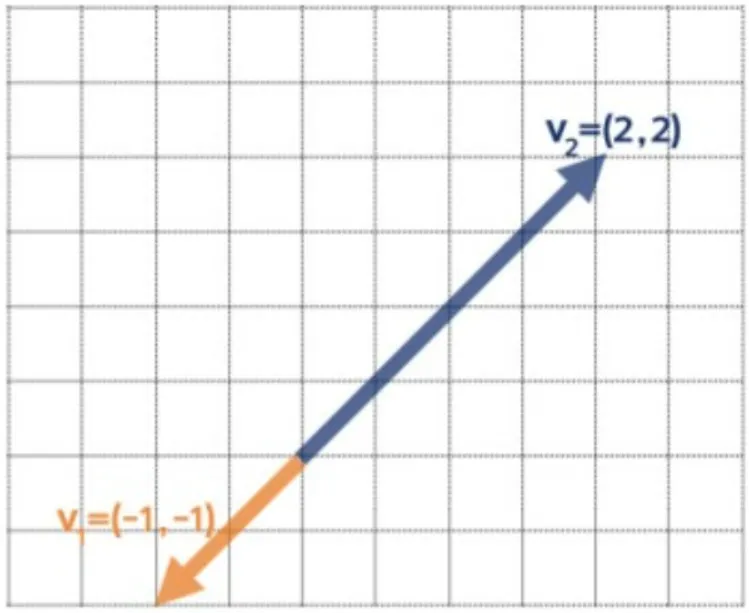
두 벡터 (1, 1)과 (2, 2)는 일차독립인가?
◦
c₁(1,1) + c₂(2,2) = (c₁ + 2c₂,c₁ + 2c₂ )에서
c₁ = -2, c₂ = 1 이면 c₁(1,1) + c₂(2,2) = 0이면서
c₁ 과 c₂가 0이 아니므로 주어진 두 벡터는 일차종속
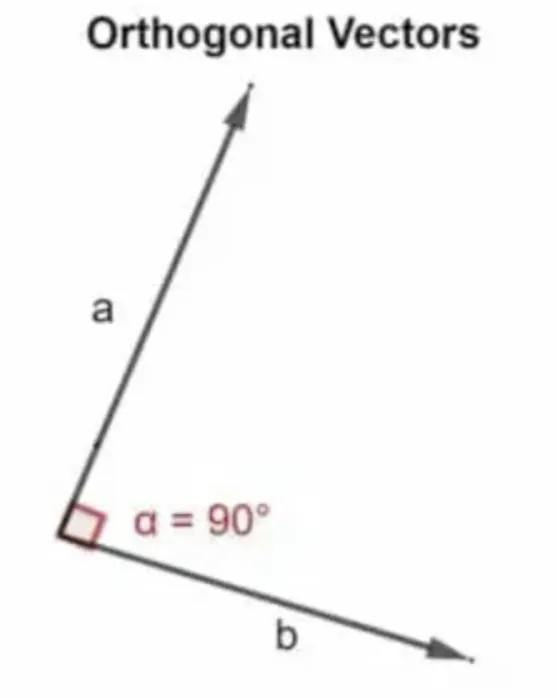
직교
•
두 벡터가 이루는 각도가 90도인 상태
•
두 벡터의 내적이 0인 상태를 의미
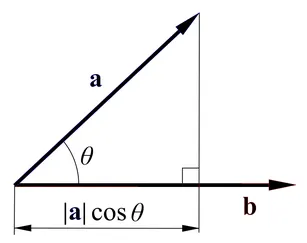
내적 : 벡터를 수처럼 곱하는 개념(방향이 일치하는 정도)
한 벡터를 다른 벡터로 정사영(벡터 그림자)시켜서, 그 벡터의 크기를 곱한다.
두 벡터가 이루는 각이 90도일 땐, 일치하는 정도가 없기 때문에 내적의 값은 0
내적의 결과값 ⇒ 스칼라
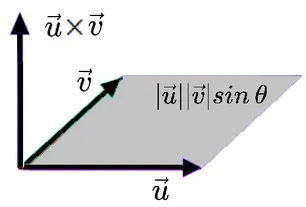
외적 : 벡터를 수처럼 곱하는 개념
방향은 곱하는 두 벡터에 수박하고, 크기는 두 벡터가 이루는 정사각형의 넓이
외적의 결과값 ⇒ 벡터
