.gif&blockId=11b00c82-b138-8050-a58b-dcbceda2ef8f)
트리란?
•
그래프의 하위 개념
•
방향성이 있는 연결된 비순환 그래프
•
계층 구조를 지니고 있다.
디렉토리 폴더 구조가 가장 흔한 예시
폴더에서 폴더로 한 계층씩 이동하며 마지막 파일을 찾는 구조
노드 = 폴더, 경로 = 엣지, 파일 = 리프노드가 가지는 데이터
트리의 특징
•
그래프는 정점들과 간선들로 이루어진 추상적인 자료구조
정점 : 위치, 노드
노드 : 위치 간의 관계 (노드를 연결하는 선)(link, branch
노드로 이루어진 자료 구조
1.
트리는 하나의 루트 노드를 갖는다.
2.
루트 노드는 0개 이상의 자식 노드를 갖고 있다.
3.
그 자식 노드 또한 0개 이상의 자식 노드를 갖고 있고, 이는 반복적으로 정의된다.
•
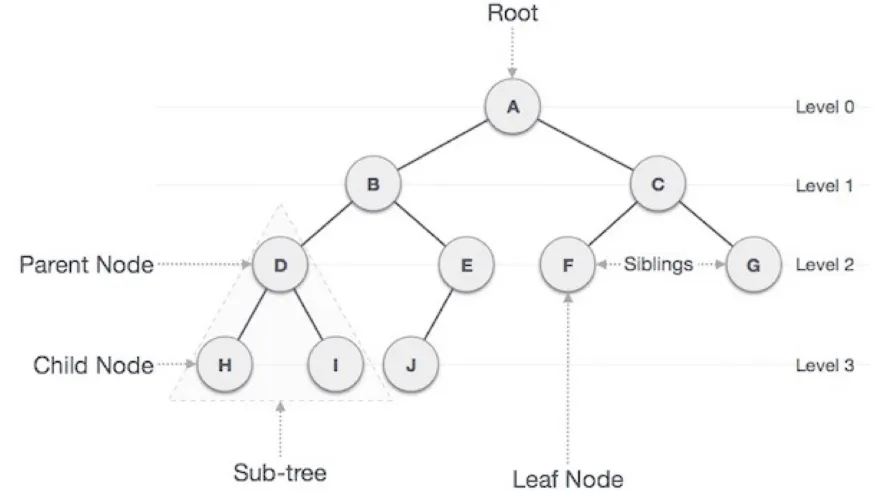
루트 노드(root node): 부모가 없는 노드, 트리는 하나의 루트 노드만을 가진다.
•
단말 노드(leaf node): 자식이 없는 노드, ‘말단 노드’ 또는 ‘잎 노드’라고도 부른다.
•
내부(internal) 노드: 단말 노드가 아닌 노드
•
간선(edge): 노드를 연결하는 선 (link, branch 라고도 부름)
•
형제(sibling): 같은 부모를 가지는 노드
•
노드의 크기(size): 자신을 포함한 모든 자손 노드의 개수
•
노드의 깊이(depth): 루트에서 어떤 노드에 도달하기 위해 거쳐야 하는 간선의 수
•
노드의 레벨(level): 트리의 특정 깊이를 가지는 노드의 집합
•
노드의 차수(degree): 하위 트리 개수 / 간선 수 (degree) = 각 노드가 지닌 가지의 수
•
트리의 차수(degree of tree): 트리의 최대 차수
•
트리의 높이(height): 루트 노드에서 가장 깊숙히 있는 노드의 깊이
Red-Black Tree
•
AVL tree, Splay tree와 같은 Self-balanced Binary Search Tree
•
모든 노드를 빨간색/검정색으로 표현
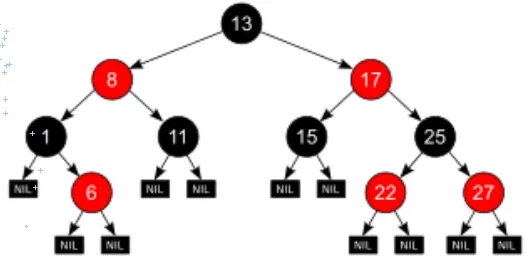
R-B Tree 만족 조건
1.
모든 노드는 빨간색 혹은 검은색
2.
루트 노드는 검은색
3.
모든 NIL은 검은색
NIL : null leaf, 자료를 갖지 않고 트리의 끝을 나타내는 리프 노드
4.
빨간색 노드의 자식은 반드시 검은색
== No Double Red(빨간색 노드가 연속으로 나올 수 없다)
5.
모든 리프 노드에서 Black Depth는 동일
== NIL에서 루트 노드까지 가는 경로에서 만나는 검은색 노드의 개수가 동일
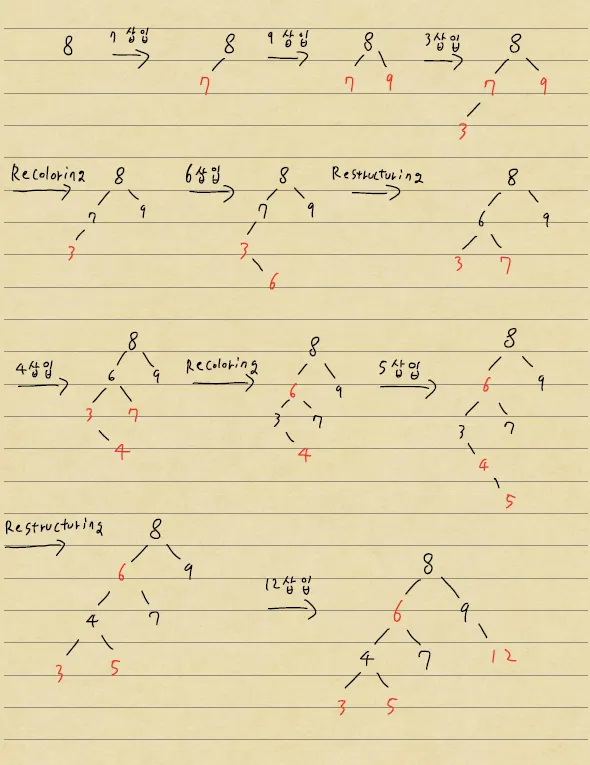
R-B Tree 삽입 과정
1.
R-B 트리의 새로운 노드는 항상 빨간색으로 삽입
•
Double Red 현상이 발생하여 4번 조건에 위배
2.
위 문제를 해결하기 위해 2가지 전략을 사용
N(New) : 새로 삽입할 노드
P(Parent) : 부모 노드
G(Grand Parent) : 조상 노드
U(Uncle) : 삼촌 노드
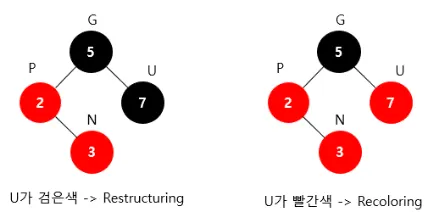
a.
U가 검은색일 경우 ⇒ Restructuring 수행
b.
U가 빨간색일 경우 ⇒ Recoloring 수행
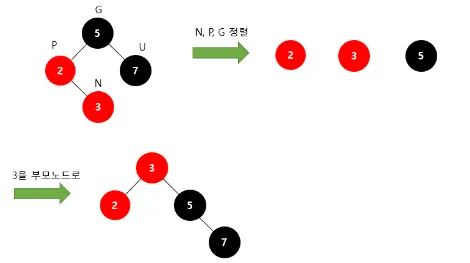
Restructuring(재구조)
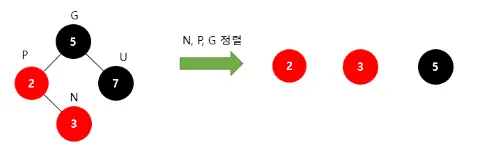
1.
새로운 노드(N), 부모 노드(P), 조상 노드(G)를 오름차순으로 정렬
2.
셋 중 중간값을 부모로 만들고 나머지 둘을 자식으로 변경
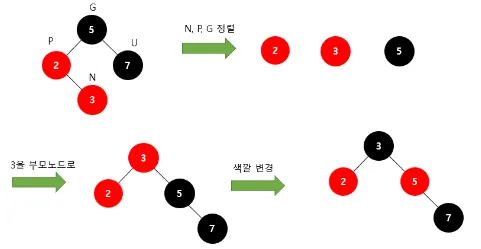
3.
새로 부모가 된 노드를 검은색으로 만들고 나머지 자식들을 빨간색으로 변경
4.
새롭게 부모가 된 3을 검은색으로 변경
5.
나머지 두 자식노드인 2,5의 색을 빨간색으로 변경하면 해결
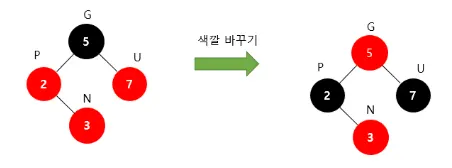
Recoloring (재색칠)
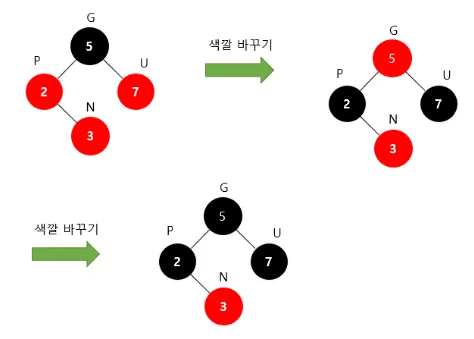
1.
새로운 노드(N)의 부모(P)와 삼촌(U)을 검은색으로 바꾸고 조상(G)을 빨간색으로 변경
a.
조상(G)이 루트 노드라면 검은색으로 변경
b.
조상(G)을 빨간색으로 바꿨을 때 또다시 Double Red가 발생한다면 또다시Restructuring 혹은 Recoloring을 진행해서 Double Red 문제가 발생하지 않을 때까지 반복
