Search

XAI : 설명 가능한 인공지능

대분류
인공지능/데이터
소분류
ML/DL 정리 노트
유형
머신 러닝
부유형
Advanced ML
주요 레퍼런스
https://velog.io/@sjinu/%EA%B0%9C%EB%85%90%EC%A0%95%EB%A6%ACSHAPShapley-Additive-exPlanations
최종 편집 일시
2024/10/30 04:49
생성 일시
2024/08/20 01:06
13 more properties

XAI(Explainable Artificial Intelligence)

•
설명 가능한 인공지능
•
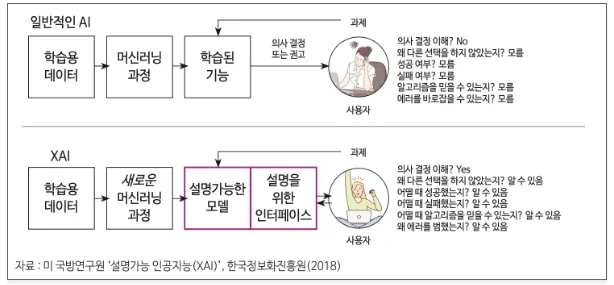
인공지능의 행위와 도출한 결과를 사람이 이해할 수 있는 형태로 설명하는 방법론과 분야
•
흔히 인공지능 기술은 복잡한 일련의 과정을 통해 결론을 도출하나, 그 과정을 설명할 수 없는 블랙박스로 여겨진다.
•
XAI는 이에 반하는 개념으로 인공지능의 불확실성을 해소하고 신뢰성을 높이는 역할을 하여, 최근 연구가 활발하게 이루어지는 분야이다.
•
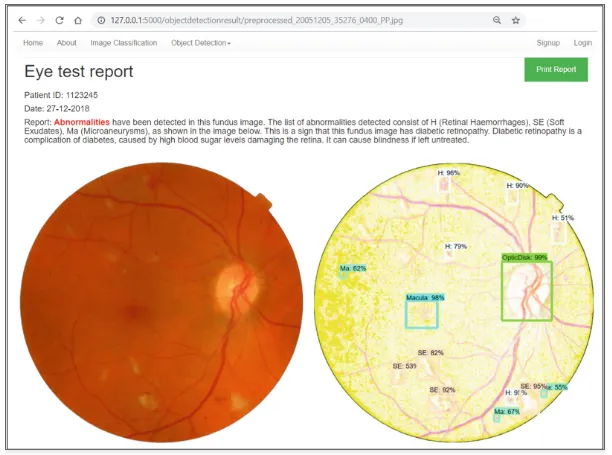
적용 사례

SHAP vs SAGE

•
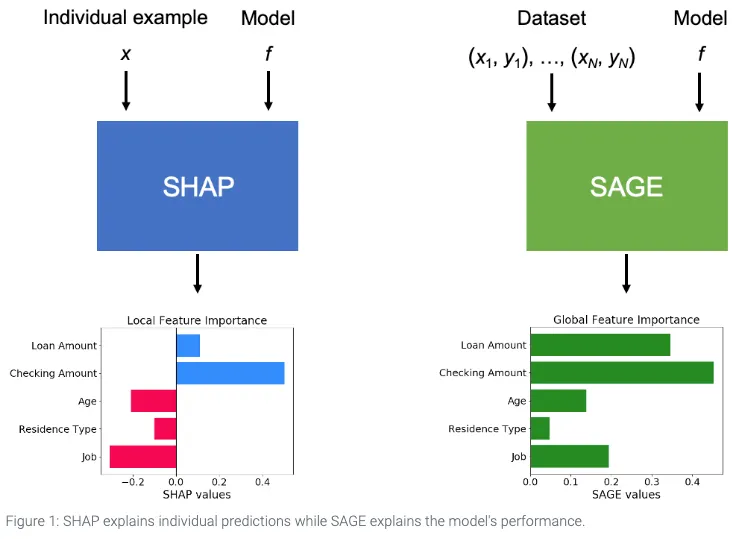
SHAP
◦
how much does each feature contribute to this individual prediction?
→ 각 피쳐들이 개별 예측에 얼마나 기여를 하였는지?
•
SAGE (Shapley Additive Global importancE)
◦
how much does the model depend on each feature overall?
→ 모델 학습시 각 피쳐들에 얼마나 의존하였는가?

SAGE(Shapley Additive Global importancE)

•
특성의 전역적인 중요도(Global Importance)를 측정하는 방법

측정 방법

•
SAGE는 Shapley 값을 이용해 특성의 기여도를 계산하는데, 이는 협력 게임 이론에서 각 참여자가 협력에 기여한 정도를 공정하게 분배하는 방식이다.
•
SAGE는 모든 데이터 포인트에 대해 Shapley 값을 계산한 후, 각 특성에 대해 전역적으로 평균화하여 중요도를 평가한다.
•
즉, SAGE는 모델의 전체 데이터에서 특성이 예측 성능에 얼마나 기여하는지를 측정하며, 이는 모델의 전역적인 특성 중요도를 평가하는 데 유용하다.

학습

from lightgbm import LGBMClassifier, plot_importance model = LGBMClassifier(random_state = random_state).fit(X_tr,y_tr)
Python
복사

평가

from sklearn.metrics import roc_auc_score pred = model.predict_proba(X_te)[:,1] > roc_auc_score(y_te, pred) 0.8821106821106821
Python
복사

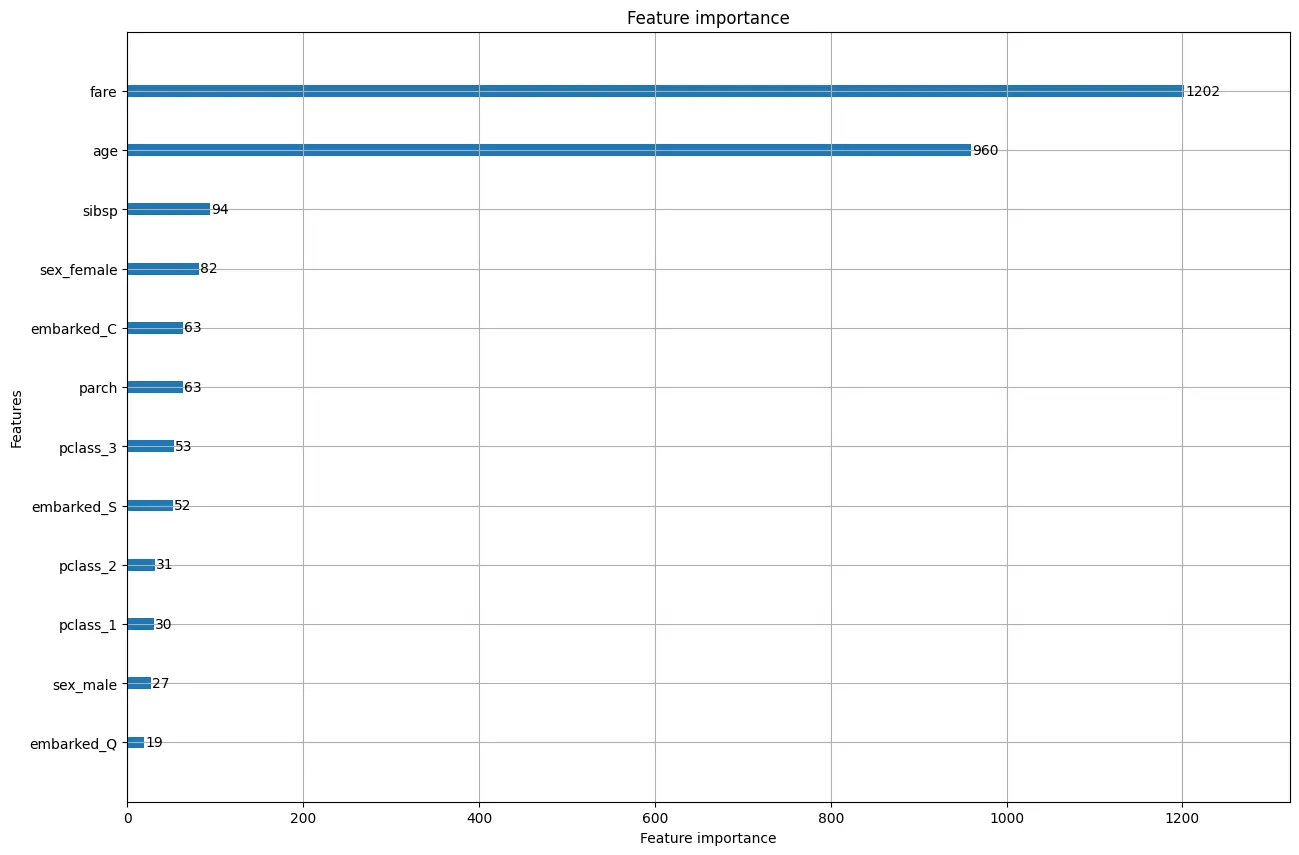
주요 파라미터 확인

import matplotlib.pyplot as plt fig, ax = plt.subplots(figsize = (15,10)) plot_importance(model,ax=ax) plt.show()
Python
복사

SHAP(Shapley Additive exPlanations)

•
Shapley Value와 피쳐간 독립성을 핵심 아이디어로 사용하는 기법
•
Shapley Value는 게임 이론을 바탕으로 각 피쳐의 기여도를 계산하는 방법
•
SHAP의 목적은 예측에 대한 각 피쳐의 기여도를 계산하여 관측치(X)의 예측값을 설명 하는것

Shapley Value - 여기서 플레이어는 Feature

1.
모든 부분집합 S⊆N∖{i}S \subseteq N \setminus \{i\}에 대해 반복한다.
2.
모든 기여도를 합산하여 플레이어 ii의 Shapley값을 계산한다.
ϕi(v)=∑S⊆N∖{i}∣S∣!(n−∣S∣−1)!n!⋅(v(S∪{i})−v(S))\phi_i(v) = \sum_{S \subseteq N \setminus \{i\}} \frac{|S|!(n - |S| - 1)!}{n!} \cdot \left( v(S \cup \{i\}) - v(S) \right)
•
ϕi(v)\phi_i(v): 플레이어 ii의 Shapley 값
→ 즉, 플레이어 ii가 전체 협력에서 기여하는 가치를 나타낸다.
•
NN: 전체 플레이어의 집합, 참여자
•
ii: 특정 플레이어 = 특성(feature)
•
SS: 플레이어 ii를 제외한 모든 플레이어의 부분집합
→ 즉, S⊆N∖{i}S\subseteq N \setminus \{i\}는 플레이어 ii를 제외한 가능한 모든 조합을 의미
•
∣S∣|S| : 집합 SS에 속한 플레이어의 수
•
v(S)v(S): 집합 SS가 협력했을 때의 가치, v=valuev = value
→ 즉, SS에 속한 플레이어들이 협력했을 때 발생하는 이득 또는 결과를 의미
•
v(S∪{i})−v(S)v(S \cup \{i\}) - v(S): 플레이어 ii가 집합 SS에 추가됨으로써 기여한 추가적인 가치
◦
SS에 속한 플레이어들이 협력하는 상황에서 플레이어 ii가 추가로 협력했을 때, 추가적으로 얻는 이득을 계산한다.
•
∣S∣!(n−∣S∣−1)!n!\frac{|S|!(n - |S| - 1)!}{n!}: 각 부분집합이 발생할 확률을 의미하는 가중치
◦
이 가중치는 플레이어 i i가 특정 부분집합에 포함될 확률을 공정하게 반영한다.
◦
Shapley 값은 모든 가능한 플레이어 조합에서 기여한 값을 공평하게 계산하기 위해 이 가중치를 사용한다.

Feature Importance와의 차이

피처 중요도 

•
예측에 가장 큰 영향을 주는 변수를 퍼뮤테이션(Permutation)하며 찾는 기법.
•
피처의 변화가 예측에 주는 영향력을 계산함으로써 피처 영향력을 측정하지만, 퍼뮤테이션의 정도와 에러에 기반한 추정 한계 때문에 알고리즘 실행 시마다 중요도가 다를 수 있다.
•
또한, 피처 중요도는 ‘피처 간 의존성’을 간과한다.
(피처 간 상관관계가 존재하는 모델은 사용을 지양해야 한다).

부분 의존성 플롯(PDP)

•
관심 피처를 조정한 값을 모델에 투입해 예측값을 구하고 평균을 낸다.
•
부분 의존성 플롯은 3차원까지의 관계만 표시할 수 있는 한계를 가진다.
(4차원 이상의 플롯은 할 수 없어 결과가 왜곡될 수 있다)

SHAP란?

Shapley Value의 조건부 기대값

fx(z′)=f(hx(z′))=E[f(z)∣zS]fx(z′)=f(hx(z′))=E[f(z)∣zS]
•
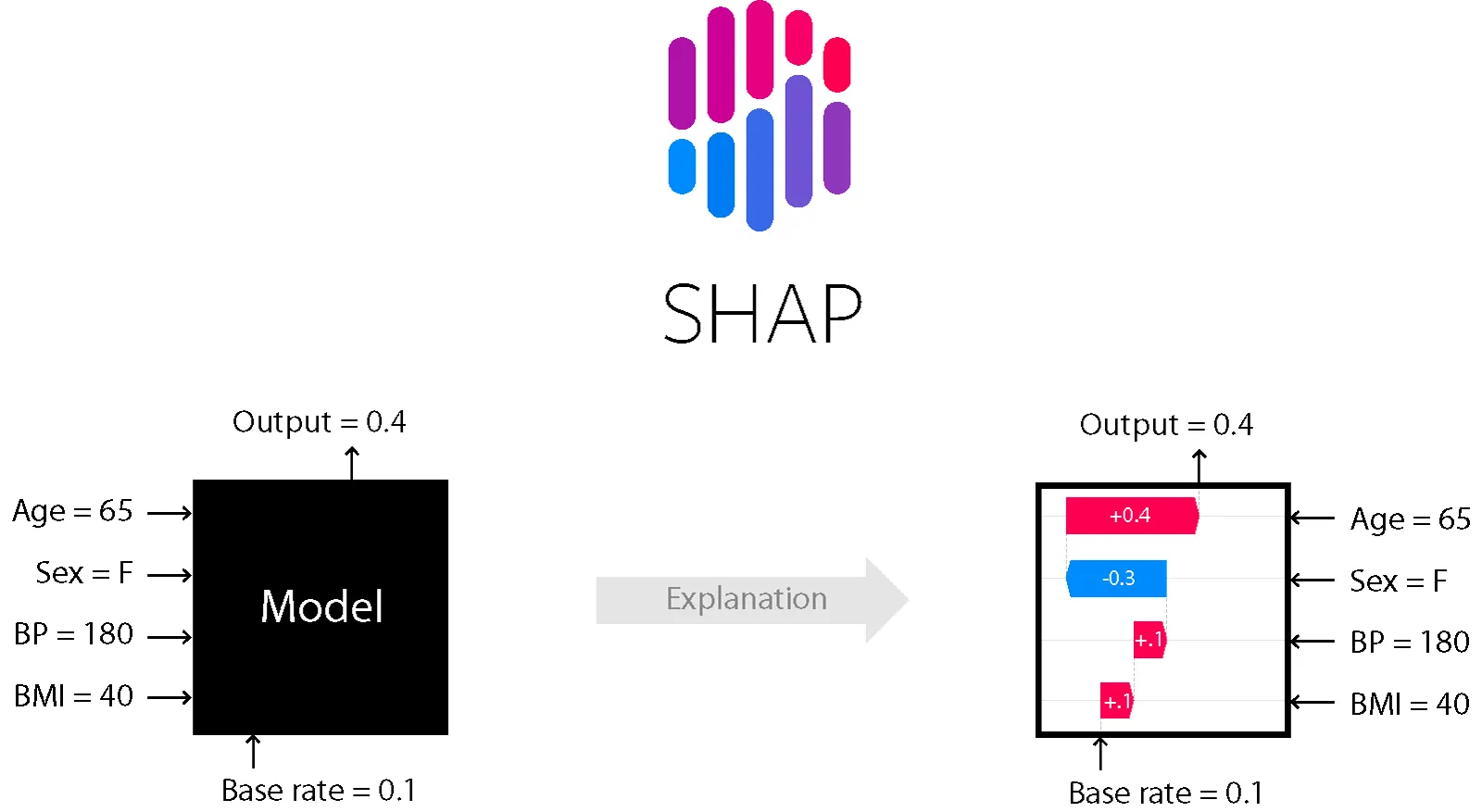
오른쪽 화살표(파란색) : 원점으로부터 f(x)가 높은 예측 결과를 낼 수 있게 도움을 주는 특성
•
왼쪽 화살표(빨간색)은 f(x) 예측에 방해가 되는 요소
•
SHAP는 Shapley value (데이터 한 개에 대한 설명, Local)을 기반으로, 데이터 셋의 ‘전체적인 영역’에 대한 해석이 가능하다(Global)

Shapley Value를 사용하여 Additive Method를 만족시키는 설명 모델

•
Additive Method(가법적 방법) : 모델의 예측을 개별적인 특성(Feature)의 기여도를 더한 값으로 설명하는 방법
f(x)=ϕ0+∑i=1Mϕixif(x) = \phi_0 + \sum_{i=1}^{M} \phi_i x_i
◦
f(x)f(x): 모델의 최종 예측값.
◦
ϕ0\phi_0: 기준값(base value), 모델이 아무런 특성 정보 없이 예측할 때의 출력값.
◦
ϕi\phi_i: 각 특성 i의 기여도 → 즉 해당 특성이 모델 예측에 얼마나 기여했는지를 나타낸다.
◦
xix_i: 특성 i의 값.
◦
MM: 전체 특성의 개수.
•
대표적인 Additive Methods
◦
Shapley 값 (Shapley Value):
▪
협력 게임 이론에서 유래한 방법으로, 각 특성의 기여도를 공정하게 계산한다.
▪
이는 모델이 예측한 값을 특성의 기여도 합으로 분해할 수 있는 방법이다.
◦
LIME (Local Interpretable Model-agnostic Explanations):
▪
특정 입력 데이터에 대해 모델이 어떻게 예측했는지 설명하기 위해 특성의 기여도를 분석하는 방법이다.
▪
LIME은 모델에 독립적이므로 어떤 모델이든 사용할 수 있다.
◦
SHAP (SHapley Additive exPlanations):
▪
Shapley 값을 기반으로 한 XAI 방법
▪
각 특성의 기여도를 더한 값이 모델의 예측값을 나타낸다.
▪
SHAP은 Shapley 값을 계산하는 효율적인 방법을 제공한다.

모델 ff의 특징에 따른 처리 방법

1.
Kernel SHAP : Linear LIME + Shapley Value
•
모델에 구애받지 않는(model-agnostic) 방법
•
선형 회귀 모델이나 복잡한 비선형 모델 모두에 적용 가능
•
Linear LIME과 Shapley Value를 결합한 방식
•
LIME과 비슷한 방식으로 데이터를 샘플링하고, 각 샘플에 대한 특성의 기여도를 Shapley 값을 통해 계산한다.
•
특징
◦
모델 불가지론적이므로 모든 모델에 적용할 수 있다. 모델이 블랙박스처럼 동작할 때도 설명이 가능하다.
◦
계산 비용이 큼: 모든 가능한 특성 조합을 고려해야 하므로, 복잡한 모델이나 많은 특성이 있는 경우 계산 비용이 높아질 수 있다.
2.
Tree SHAP : Tree Based Model
•
트리 기반 모델(Tree-based Model)에서 SHAP 값을 빠르고 효율적으로 계산하기 위한 방법
•
랜덤 포레스트(Random Forest), XGBoost, LightGBM과 같은 트리 기반 모델에 최적화
•
특징
◦
빠른 계산 속도: 트리 모델의 특성을 활용하여 특성 조합을 효율적으로 탐색하고, SHAP 값을 더 빠르게 계산할 수 있다.
◦
트리 기반 모델에 최적화되어 있으므로, 다른 유형의 모델에는 직접 사용할 수 없다.
3.
Deep SHAP : Deeplearning based model
•
딥러닝 기반 모델(Deeplearning based model)에 적용할 수 있는 SHAP 방법
•
DeepLIFT(Deep Learning Important FeaTures)의 아이디어를 결합하여 효율적인 계산을 가능하게 한다.
•
각 뉴런에 대한 기여도를 추적하여 SHAP 값을 계산
•
각 레이어를 거치면서 특성들이 어떻게 기여하는지를 분석해, 딥러닝 모델에서도 SHAP 값을 효율적으로 계산할 수 있도록 한다.
•
특징
◦
딥러닝 모델의 복잡한 비선형 구조에서도 SHAP 값을 계산할 수 있게끔 설계
◦
DeepLIFT와 Shapley 값을 결합한 형태
◦
딥러닝 모델의 복잡한 구조를 반영하기 때문에 계산 비용이 크다.

실습

설치

!pip install shap !pip install scikit-image
Python
복사
import shap import skimage explainer = shap.TreeExplainer(model) # 학습된 모델을 넣는다. shap_values = explainer.shap_values(X_te) > shap_values[1].shape , X_te.shape ((13,), (179, 13))
Python
복사

force_plot

•
각 데이터마다 feature의 영향력을 보여준다.
•
빨간색은 긍정적인 영향, 파란색은 부정적인 영향
# 첫번째 데이터만 분석 shap.initjs() shap.force_plot(explainer.expected_value,shap_values[0,:],X_te.iloc[0,:])
Python
복사
# 두번째 데이터만 분석 shap.initjs() shap.force_plot(explainer.expected_value,shap_values[1,:],X_te.iloc[1,:])
Python
복사
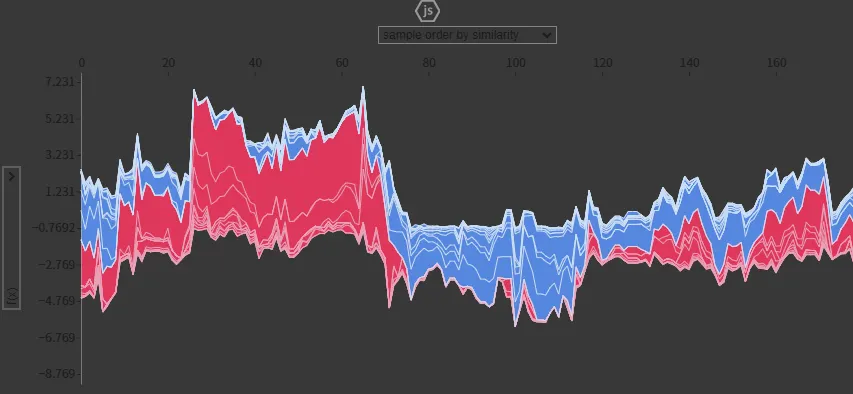
# 전체 데이터 분석 shap.initjs() shap.force_plot(explainer.expected_value, shap_values, X_te)
Python
복사

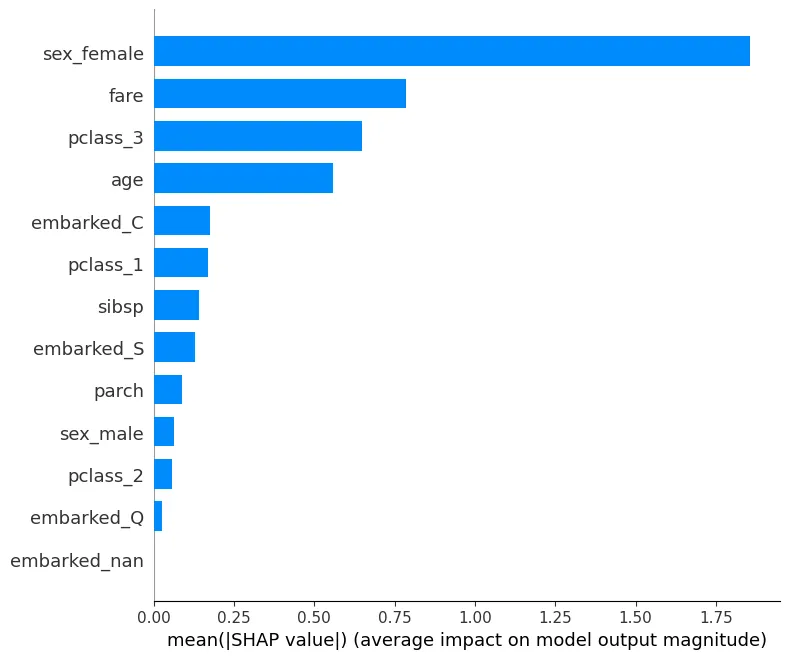
summary_plot

•
force_plot의 전체 데이터의 영향력을 간단하게 시각화하여 보여줌
•
sex_female은 target과 양의 상관관계를 pclass_3는 target과 음의 상관관계를 나타낸다고 해석할 수 있음
shap.summary_plot(shap_values,X_te)
Python
복사
shap.summary_plot(shap_values,X_te, plot_type="bar")
Python
복사

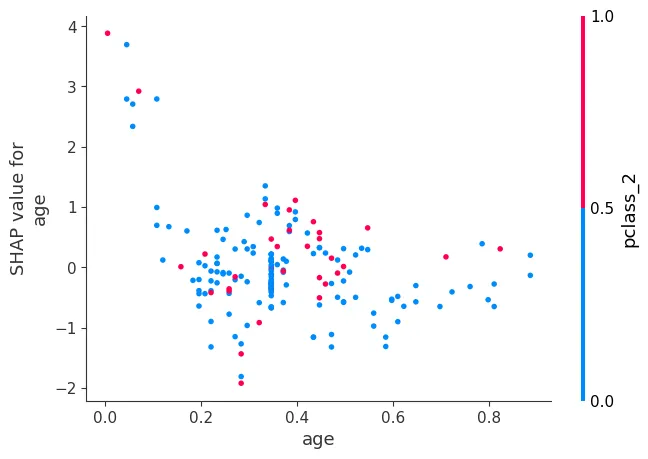
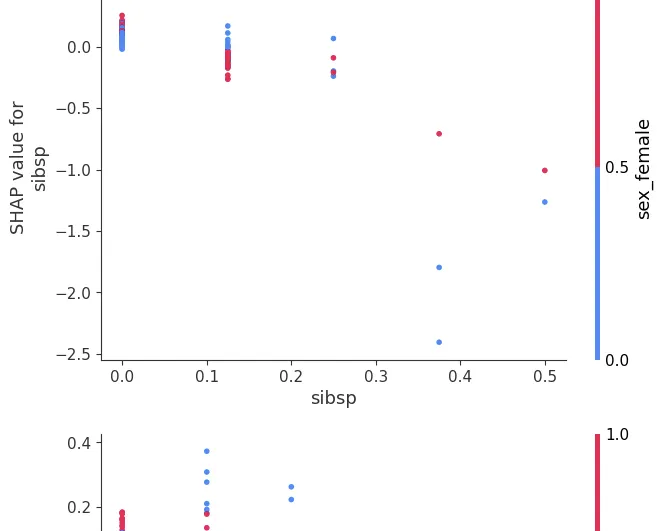
dependence_plot

•
특정 변수에 대한 영향도 파악
shap.dependence_plot("age", shap_values, X_te,interaction_index=None)
Python
복사
shap.dependence_plot("age", shap_values, X_te,interaction_index="auto")
Python
복사
for col in X_te.columns: shap.dependence_plot(col, shap_values, X_te)
Python
복사