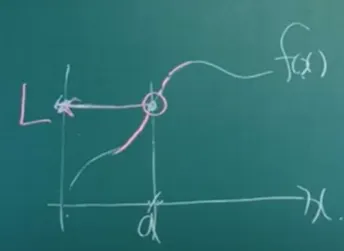삼각함수(sin, cos, tan)
•
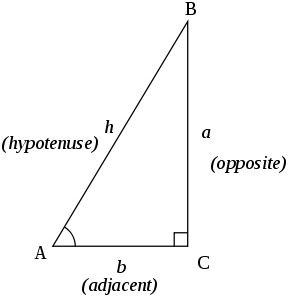
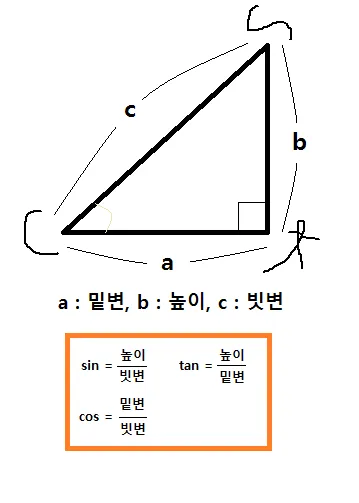
빗변/기울기(hypotenuse), 높이(opposite), 밑변(adjacent)
•
사인(sine/sin), 코사인(cosine/cos), 탄젠트(tangent/tan)
•
코시컨트(cosecant/csc), 시컨트(secant), 코탄젠트(cotangent/cot) = sin, cos, tan의 역수
•
탄젠트의 법칙
로그 (Logarithm)
•
지수 함수의 역함수
•
로그함수 활용용도
◦
로그 함수는 단위 수가 너무 큰 값들을 바로 회귀분석 할 경우 결과를 왜곡할 우려가 있으므로 이를 방지하기 위해 사용
◦
비선형관계의 데이터를 선형으로 만들기 위해 사용
◦
독립변수와 종속변수의 변화관계에서 절대량이 아닌 비율을 확인하기 위해 사용
◦
왜도와 첨도를 줄일 수 있어 정규성이 높아진다.
왜도 : 데이터가 한쪽으로 치우친 정도
첨도 : 분포가 얼마나 뾰족한지를 나타내는 정도
로그 법칙
1.
2.
3.
4.
5.
6.
7.
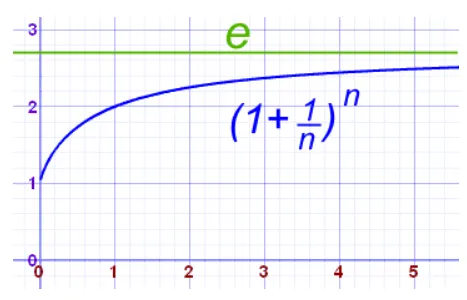
무리수 (2.718…)
•
1에 아주 조금 더한 것의 무한 제곱
x | (1 + x) ^ (1 / x) |
0.1 | 2.5937424601000023 |
0.01 | 2.7048138294215285 |
0.001 | 2.7169239322355936 |
0.0001 | 2.7181459268249255 |
0.00001 | 2.7182682371922975 |
... | ... |
0.0000000....000001 | 2.7182818284590452... |
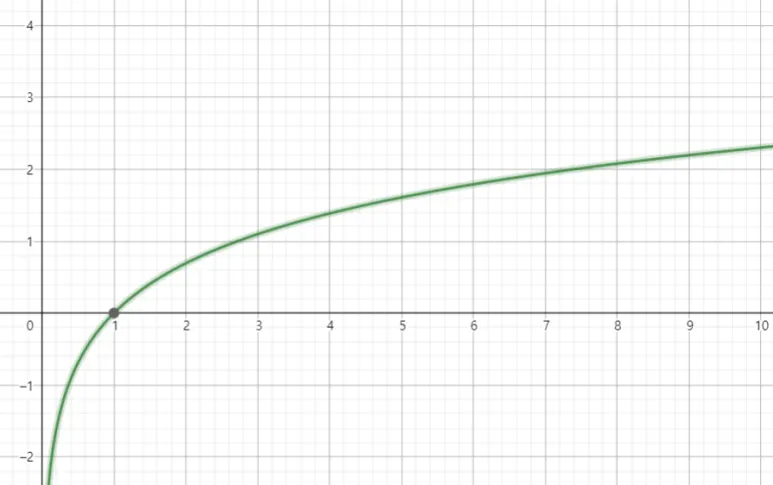
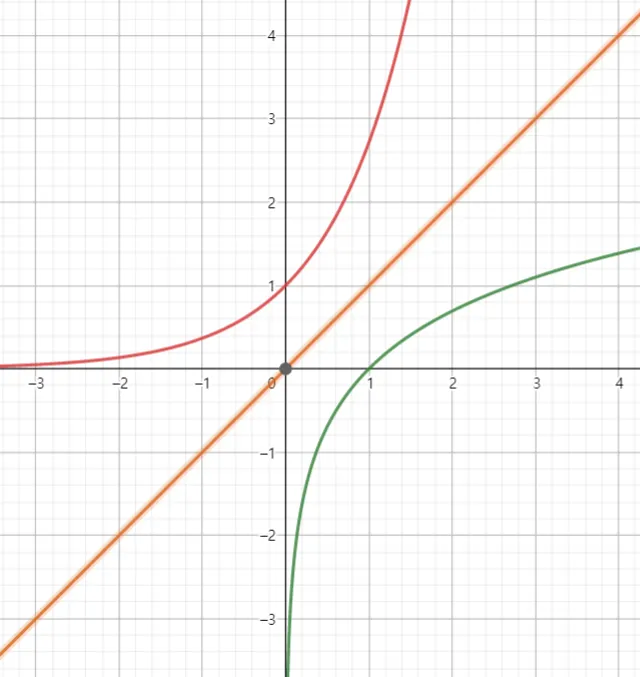
자연 로그 (natural logarithm)
•
무리수 를 밑으로 하는 로그
그래프
그래프
•
미적분 관련 계산을 할 때, 밑이 10인 상용로그 대신 이 밑이 무리수 e인 로그를 사용하면 훨씬 더 깔끔하고 단순하게 나와 자연스럽다고 하여 자연로그라고 이름이 붙여졌다고 함.
•
성질 ( 일때 )
1.
2.
3.
4.
극한
•
: x가 a랑 무진장 가까운 값일 때 f(x)가 뭐랑 무진장 가깝냐?
•
: L주변의 갭으로 어떤 양수 (입실론)을 잡더라도 요 갭 안으로 싹다 보내버릴 수 있는 a 주변 갭 (델타)가 존재하면 a에서의 극한 값은 L이다. (입실론-델타 논법)
L 주변의 갭
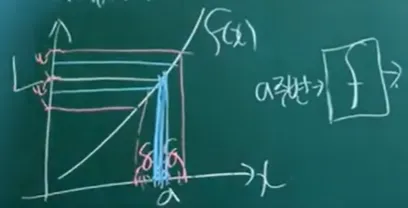
미분(델타, h)
•
순간 변화율
•
순간 기울기(그래프 상에선)
◦
접선의 기울기(정의역=)
◦
x를 a에서 h(델타)만큼 떨어진 점이라 볼 때 를 대입하여 다음과 같이 표현(변화량 = )
기울기 : / (양) \ (음)
도함수
•
주어진 함수의 각 점에서의 변화율을 나타내는 새로운 함수
•
함수의 도함수 표기법
◦
◦
◦
◦
◦
•
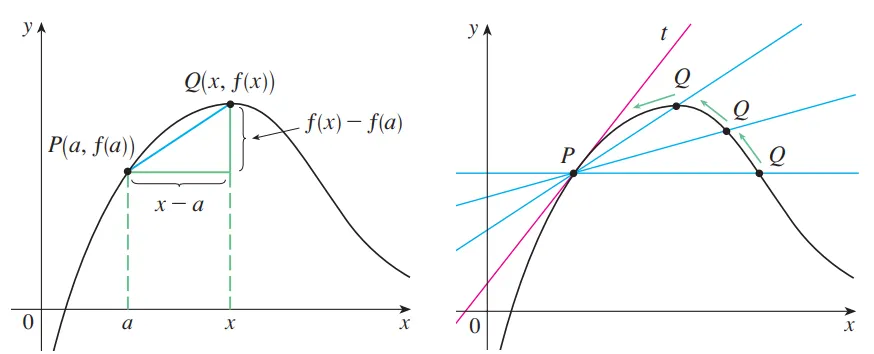
도함수의 기하학적 의미 : 위의 임의의 점 에서의 접선의 기울기
1.
(c는 상수)이면
2.
(n은 양의 정수)이면
3.
4.
5.
•
도함수 예제 풀이
◦
에서의 미분값?
◦
에서의 미분값?
미분 계수
•
에서 함수 의 접선의 기울기 ⇒ 의 에서의 미분계수 =
미분 공식
1.
연쇄 법칙
•
합성 함수
◦
일 때
•
미분 계수 구별
편미분 , 그라디언트
편미분
•
다변수 함수에 대한 미분
다변수 함수 : 독립 변수가 여러 개인 함수
•
독립변수가 한 개인 일변수 함수
•
독립변수가 두 개인 다변수 함수
◦
이변수 함수
•
변수 하나를 제외한 나머지를 모두 상수 취급한 상태로 미분을 취하는 것
•
x, y, z가 있는 다변수 함수에서 x에 대한 편미분은 y,z를 상수 취급
1.
항의 편미분
•
에서 x에 대해 편미분할 때, 는 상수로 간주
⇒ 즉, 는 미분할 때 변화하지 않는 상수로 처리
◦
원래 식:
◦
x에 대한 편미분:
•
미분 과정
◦
y^2는 상수이므로, 단순히 x의 계수로 남는다.
◦
따라서, 편미분은 y2가 된다.
2.
항의 편미분
•
에 대한 1차항
◦
원래 식:
◦
x에 대한 편미분:
•
미분 과정
◦
x에 대한 미분에서 상수 4가 남는다.
3.
항의 편미분
•
x에 대한 미분에서 상수로 간주
⇒ 따라서 미분 값은 0
◦
원래 식 :
◦
x에 대한 편미분:
•
-7y는 x에 독립적이므로 미분 값은 0
4.
결과
x에 대한 편미분은 x의 변화만 고려한 미분이다
•
표기법
◦
: 라운드(round), 파셜(partial)
◦
x에 대한 편미분일 때
▪
▪
편도함수
•
편미분에 대한 도함수
그레디언트(Gradient): 기울기
•
다변수 함수의 모든 입력값에서 모든 방향으로의 순간변화율
⇒ 공간에 대한 기울기
•
주어진 함수 의 그라디언트는 함수의 각 변수에 대한 편미분을 모은 벡터로 정의
•
다변수(n변수 스칼라) 함수 f(x,y,z)의 그라디언트 벡터 표기 (: 델 연산자)
모든 방향에 대해 모두 표기
◦
방향은x방향으로의 단위벡터
◦
방향은y방향으로의 단위벡터
◦
방향은z방향으로의 단위벡터
•
함수 의 그라디언트
1.
편미분 계산
2.
그라디언트 벡터
•
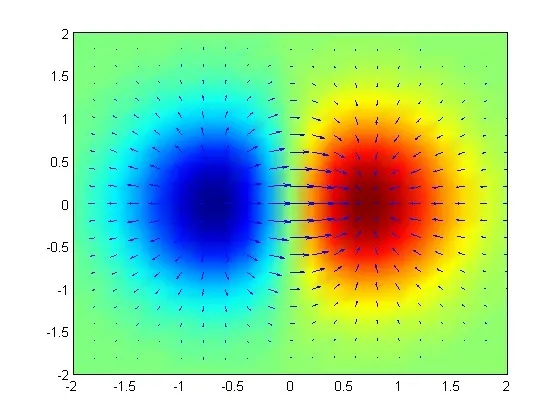
예시 벡터 그래프
◦
2변수 이상부터는 스칼라 함수에 대해서 gradient가 벡터로 구해지게 된다.
1변수의 경우 성분이 하나인 벡터로 생각 가능
◦
화살표가 그래디언트의 방향 : 함수값이 작은 부분에서 벗어나서 함수값이 큰 부분으로 가려고 하는 것
◦
빨간색으로 표시된 부분 : 함수값이 큰 부분
◦
파란색으로 표시된 부분 : 함수값이 작은 부분
확률
확률 변수
•
확률 실험을 했을 때 발생할 수 있는 결과(s)를 실수값()으로 바꿔주는 함수
◦
s(sample) : 표본공간에 속한 원소
◦
표본공간(sample space, S) : 확률실험의 결과로 나타날 수 있는 모든 결과들
◦
확률실험(pobability experiment) : 결과를 예측할 수 없는 실험
•
확률 변수가 나타날 확률 계산식
◦
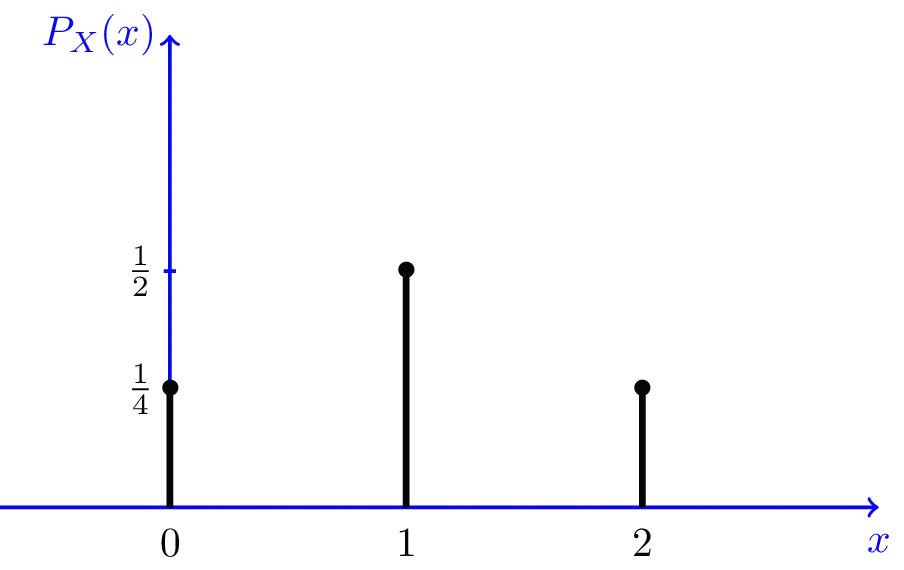
이산형 확률변수 (pmf: probability mass function)
X | 0 | 1 | 2 | sum |
P(X = x) | 1 |
▪
이산형일 경우 막대의 높이가 곧 그 점에서의 확률을 의미
◦
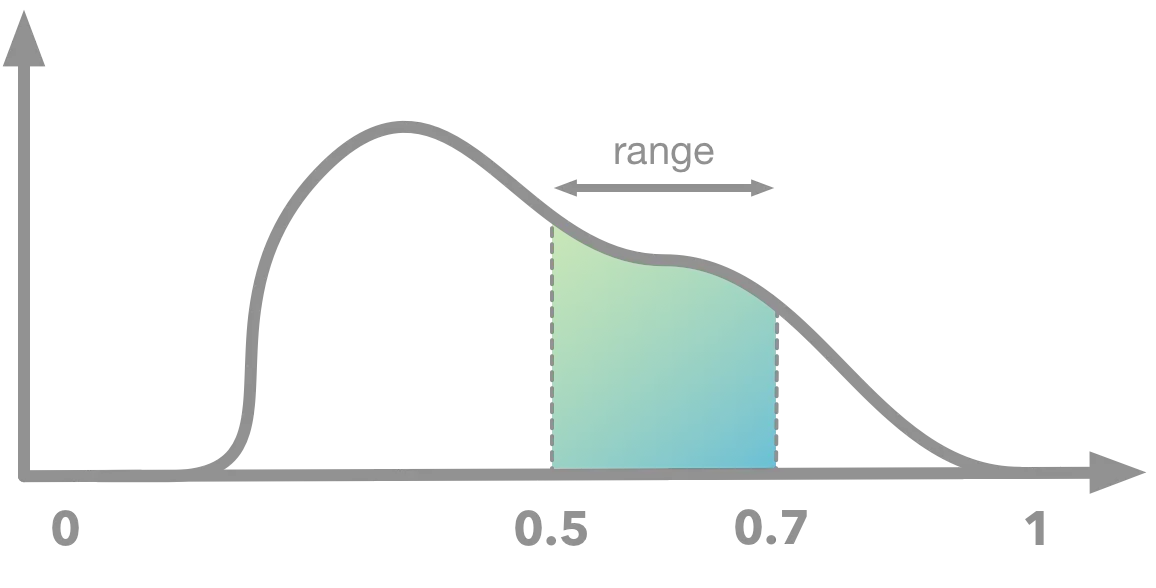
연속형 확률변수 (pdf: probability density function)
▪
연속형의 경우 P(X=x) = 0 (1/(연속형 확률변수의 가능한 값) ≈1/∞≈0≈1/∞≈0)임
▪
연속형 확률변수의 확률 = 구간의 너비
평균, 분산, 표준편차
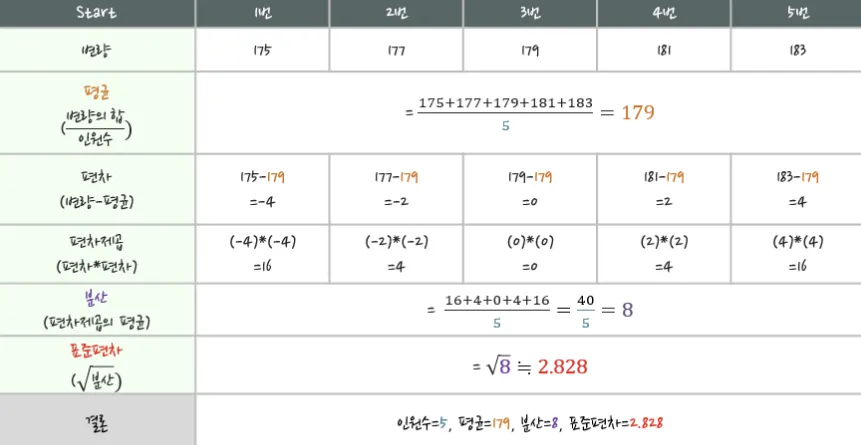
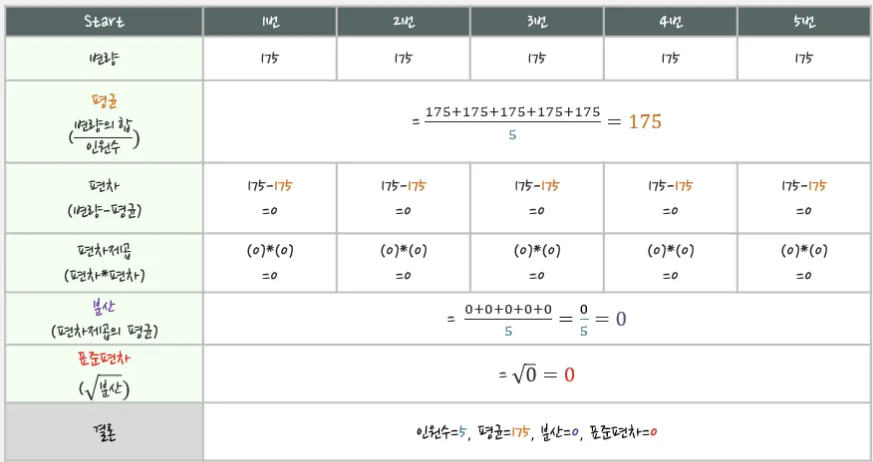
•
평균(Mean, Average) : 주어진 수의 합을 측정개수로 나눈 값, 대표값 중 하나
•
분산(Variance) : 변량들이 퍼져있는 정도, 분산이 크면 들죽날죽 불안정하다는 의미, 대표값 중 둘
•
표준편차(Standard Deviation) : 분산은 수치가 너무 크기 때문에, 제곱근으로 적당하게 줄인 값
◦
표준편차가 큰 경우, 수치들이 전반적으로 들죽날죽 지들 멋대로 쌩쇼하는구나
◦
표준편차가 작은 경우, 수치들이 고만고만 도토리 키 재듯 밋밋하구나
•
변량이 다른 경우
•
변량이 똑같은 경우
기댓값(E: Expected Value)
•
확률 변수의 기대값 = 모평균(population mean)
⇨ 확률분포(또는 모집단)의 무게 중심
•
각 사건이 벌어졌을 때의 이득과 그 사건이 벌어질 확률을 곱한 것을 전체 사건에 대해 합한 값