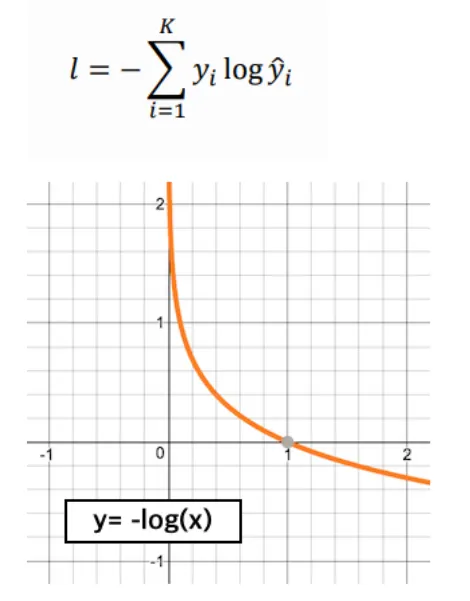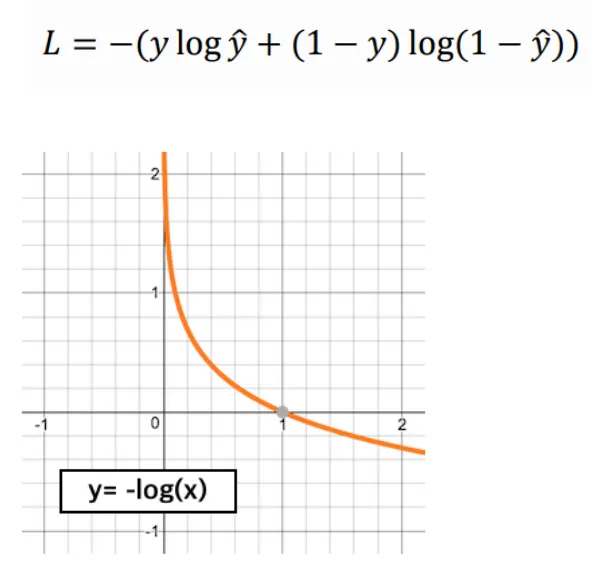Search

Deep Learning 개요

대분류
인공지능/데이터
소분류
ML/DL 정리 노트
유형
딥 러닝
부유형
기초
최종 편집 일시
2025/02/17 08:45
생성 일시
2024/09/04 02:30
14 more properties

인공지능(Artificial Intelligence)

•
사람의 지능을 만들기 위한 시스템이나 프로그램
•
딥러닝은 머신러닝에 포함되는 기술

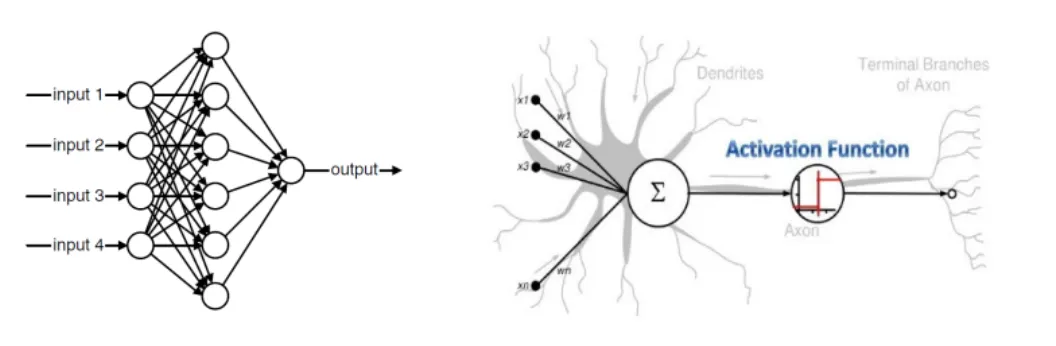
인공 신경망

•
뉴런을 모방하는 기초단위 노드(Node)
◦
각각의 신경 단위에서 많은 입력들을 조합해서 하나의 출력값으로 배출
◦
비선형 변환(활성함수)을 통해 다음 노드에 전달
•
피드 포워드(Feed-forward) 신경망
◦
입력에서 출력으로 이어지는 과정이 한방향으로 흘러 순환이 없는 신경망

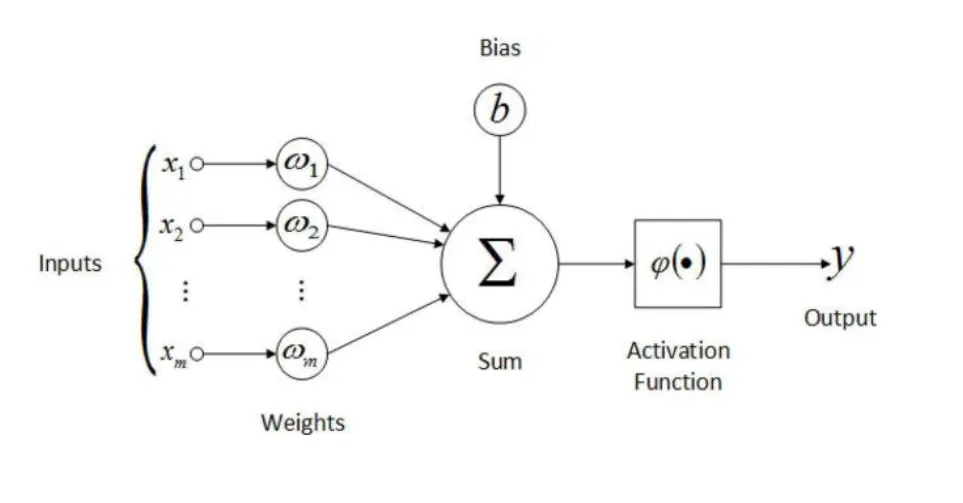
인공 뉴런(퍼셉트론)

•
w: weight(가중치)
•
b: bias(편향)
•
h(): Activation Function
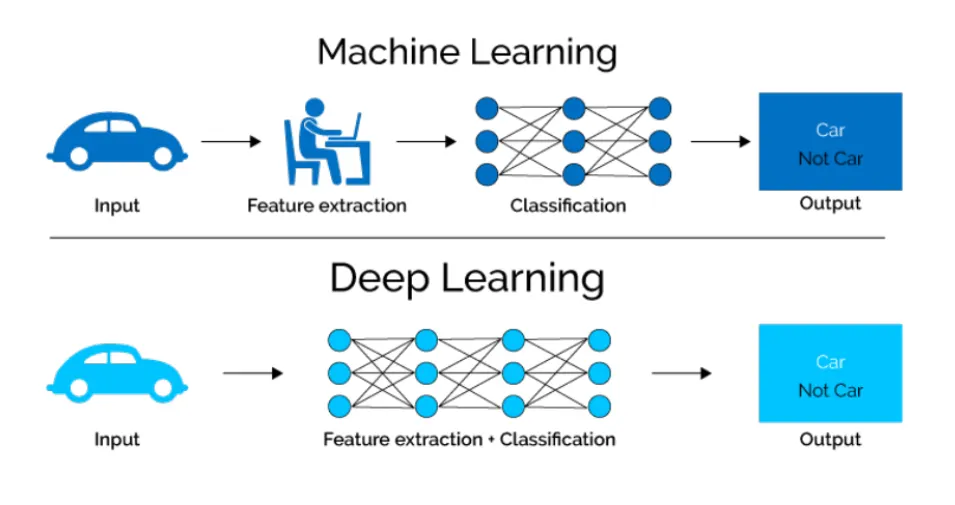
a=b+w1x1+w2x2+...+wmxmy=h(a)a = b + w_1x_1 + w_2x_2 + ... + w_mx_m \\ y = h(a)

딥러닝(Deep Learning)

•
딥러닝은 머신러닝 알고리즘 중 하나인 인공신경망을 다양하게 쌓은 것
•
인공신경망을 여러 겹으로 쌓으면 딥러닝

딥러닝은 머신러닝이 처리하기 어려운 데이터(비정형 데이터)를 더 잘 처리

딥러닝은 만능?

•
학습을 위해 상당히 많은 양의 데이터를 필요로 함
•
계산이 복잡하고 수행시간이 오래 걸림
•
이론적 기반이 없어 결과에 대한 장담이 어려움
•
블랙 박스 접근 방식

Deep Learning Everywhere

가중치와 편향

가중치(Weight)

•
가중치는 신경망에서 각 입력 데이터가 출력에 얼마나 중요한 영향을 미치는지를 결정하는 값
•
신경망의 각 뉴런은 입력을 받아 계산을 수행하고 출력으로 전달하는데, 이때 입력에 곱해지는 값이 바로 가중치
•
역할
◦
가중치는 입력 신호의 중요도를 조절
◦
높은 가중치는 해당 입력이 더 중요한 정보라는 것을 의미하고, 낮은 가중치는 덜 중요하다는 것을 의미
•
학습
◦
모델이 학습을 통해 최적의 가중치를 찾아나가면서, 입력 데이터와 출력 간의 관계를 더 잘 표현하게 된다.
◦
가중치는 학습 과정에서 계속 업데이트되며, 손실 함수(오차)를 줄이는 방향으로 조정
•
예를 들어, 하나의 뉴런에서 입력 x1,x2,x3x_1, x_2, x_3이 주어진다면, 가중치 w1,w2,w3w_1, w_2, w_3는 각 입력에 곱해져서 다음과 같은 방식으로 계산:
z=w1⋅x1+w2⋅x2+w3⋅x3z=w_1⋅x_1+w_2⋅x_2+w_3⋅x_3

편향(Bias)

•
편향은 모델이 입력 데이터가 0일 때도 출력을 내보낼 수 있도록 하는 값
→ 즉, 편향은 가중치로 곱해진 입력값에 더해지는 상수
•
신경망이 더 유연하게 학습할 수 있게 해줌
•
이는 일종의 보정 값이라고 생각할 수 있다.
◦
역할
▪
편향은 모든 입력이 0인 경우에도 뉴런이 활성화될 수 있도록 돕는다.
▪
만약 편향이 없다면, 입력이 모두 0일 때 신경망은 항상 0을 출력하게 될 것
▪
편향이 있으면 출력값을 조정할 수 있다.
◦
학습: 가중치와 마찬가지로, 편향도 학습 과정에서 업데이트되어 최적의 값을 찾는다.
•
편향이 포함된 계산은 다음과 같이 표현
z=w1⋅x1+w2⋅x2+w3⋅x3+bz=w_1⋅x_1+w_2⋅x_2+w_3⋅x_3+b

손실함수(Loss Function)

•
모델의 출력값(Output)과 정답과의 차이(오차,Error)를 의미
•
신경망이 학습할 수 있도록 해주는 지표
•
모델의 출력이 얼마나 잘못되었는지를 나타내는 지표
•
모델이 학습하는 과정은 이 손실 함수를 최소화하는 방향으로 이루어진다.
•
손실 값이 최소화 되도록 하는 가중치(weight)와 편향(bias)를 찾는 것이 학습의 목표

손실 함수의 역할

1.
오차 측정: 모델의 예측 값이 실제 값과 얼마나 차이가 나는지 측정
2.
최적화 방향 결정: 손실 함수 값이 작을수록 모델이 더 정확하게 예측하고 있는 것이므로, 손실을 줄이는 방향으로 모델의 가중치와 편향을 업데이트하는 것이 목표
3.
학습 가이드: 경사 하강법(Gradient Descent) 등의 최적화 알고리즘을 통해 손실 함수의 값을 줄이기 위한 가중치와 편향의 변화를 계산

회귀(Regression)에서의 손실함수

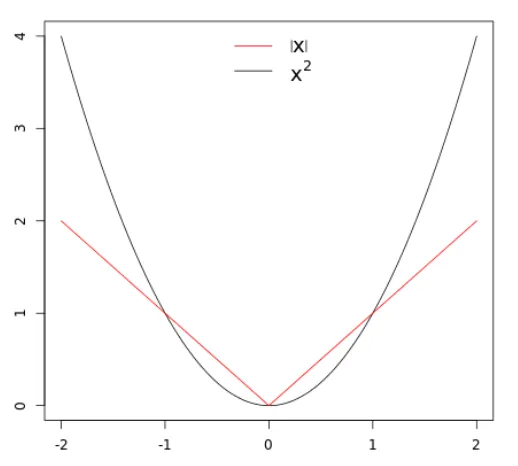
MAE:L1 Loss (Mean Absolute Error:L1, 평균 절대 오차)

•
예측 값과 실제 값의 차이를 절대값으로 계산한 후, 그 평균을 구한 값
MAE=1n∑i=1n∣yi−y^i∣MAE=\frac{1}{n}\sum^n_{i=1}|y_i-\hat{y}_i|
•
특징
◦
MSE와 달리 오차가 클 때 제곱하지 않고 절대값을 사용하므로, 큰 오차에 덜 민감하게 반응
◦
오차에 대한 직관적인 해석이 가능
◦
회귀 문제에서 사용
◦
이상치에 강건
•
주로 사용되는 문제
◦
외래치가 많지 않은 회귀 문제.
◦
예를 들어, 주택 가격 예측처럼 예상 오차가 균등하게 분포된 경우에 사용

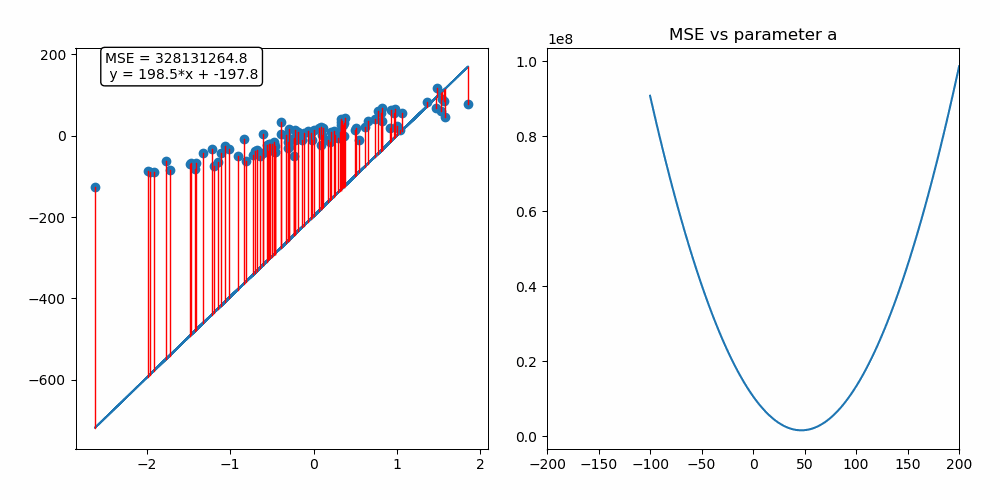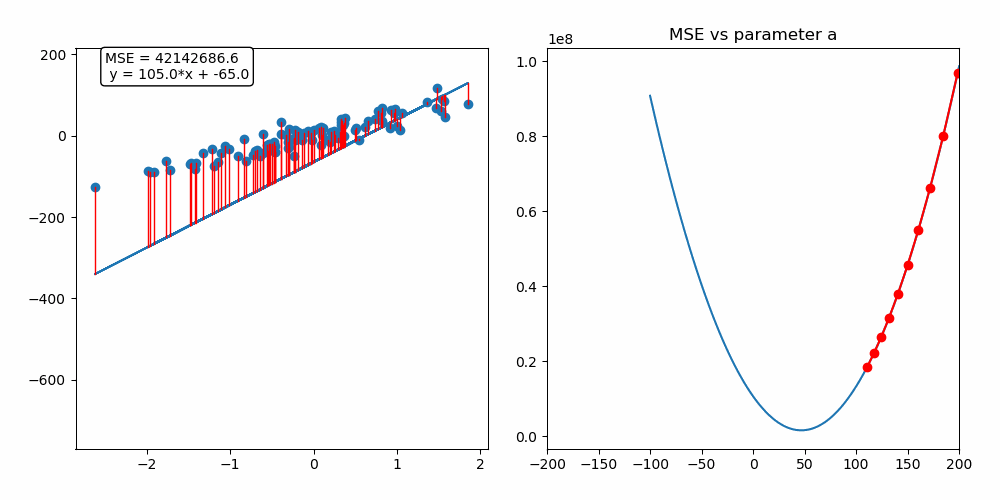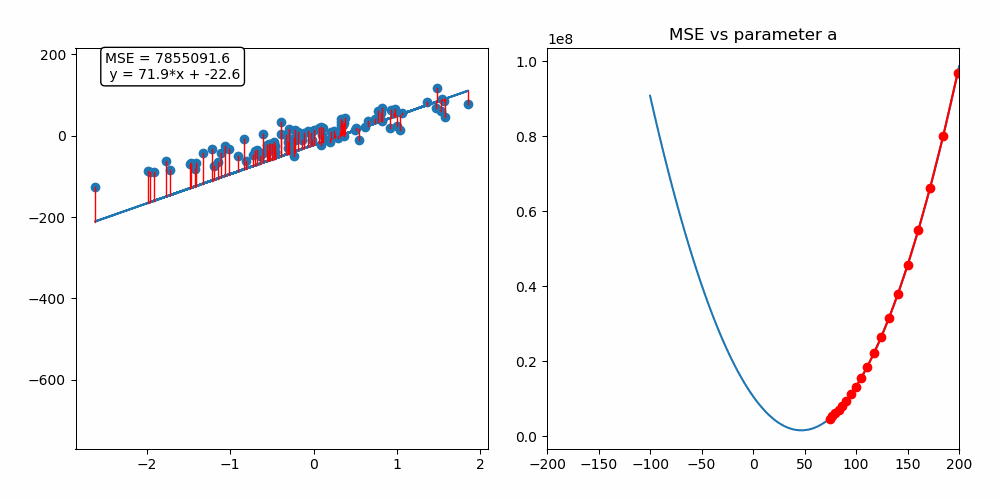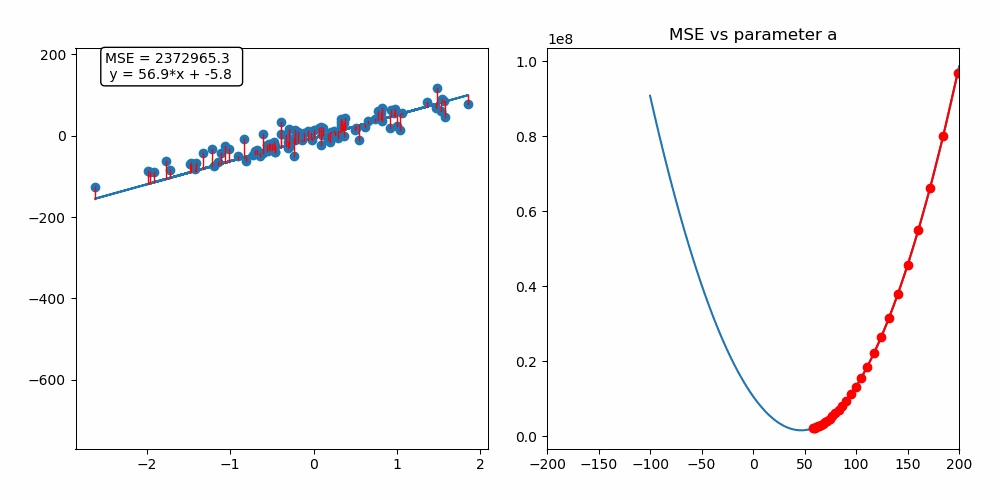
MSE:L2 Loss (Mean Squared Error:L2, 평균 제곱 오차)

•
MSE는 회귀 문제에서 많이 사용되며, 예측 값과 실제 값의 차이를 제곱한 뒤, 그 평균을 취한 값
•
제곱을 통해 큰 오차일수록 더 큰 페널티를 부여
MSE=1n∑i=1n(yi−y^i)2MSE = \frac{1}{n}\sum^n_{i=1}(y_i-\hat y_i)^2
◦
yiy_i는 실제 값
◦
y^i\hat{y}_i는 예측 값
◦
nn은 샘플의 개수
•
특징
◦
오차가 클수록 손실이 크게 증가하므로, 큰 오차에 민감하게 반응
◦
회귀 모델에서 많이 사용
◦
외래치(이상치)에 민감하다. 큰 오차가 발생하면 그 값이 제곱되기 때문에, 아주 큰 영향을 미친다.
•
주로 사용되는 문제
◦
큰 오차를 더 많이 패널티를 주고 싶을 때.
◦
예를 들어, 날씨 예측이나 주가 예측처럼 큰 오차가 발생하면 중요한 경우에 많이 사용

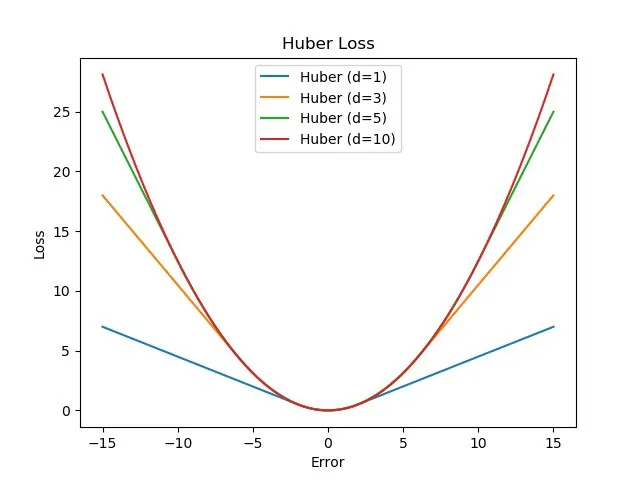
Huber Loss

•
MSE와 MAE의 장점을 결합한 손실 함수
◦
큰 오차에 대해서는 MSE처럼 반응하고, 작은 오차에 대해서는 MAE처럼 반응
◦
큰 오차에 덜 민감하면서도, 작은 오차에 대해서는 세밀하게 반응하는 특성을 보유
Lδ(a)={12a2x=for∣a∣≤δδ(∣a∣−12δ)otherwise>0L_{\delta}(a)= \begin{cases}\frac{1}{2}a^2 & x = for |a|\leq \delta \\ \delta(|a|-\frac{1}{2}\delta) & otherwise > 0\end{cases}
▪
aa는 예측 값과 실제 값의 차이(오차)
▪
δδ는 임계값
▪
작은 오차 (∣오차∣≤δ|오차| ≤ δ): MSE처럼 오차의 제곱을 사용.
▪
큰 오차 (∣오차∣>δ|오차| > δ): MAE처럼 오차의 절대값을 사용.
•
특징
◦
큰 오차에 대한 민감도를 조정할 수 있는 파라미터 δ\delta를 가지고 있다.
◦
회귀 문제에서 자주 사용
◦
외래치(Outliers) 처리: MSE는 큰 오차(외래치)에 민감하게 반응하는 반면, MAE는 외래치에 덜 민감하지만, 작은 오차에 대한 민감도가 떨어진다. Huber Loss는 작은 오차는 MSE처럼 세밀하게 처리하고, 큰 오차는 MAE처럼 외래치의 영향을 줄이는 방식으로 두 가지 방법의 균형을 맞춘다.
◦
효율성: 외래치가 있는 데이터셋에서 MSE와 MAE의 단점을 보완하면서 성능을 향상시키기 위해 Huber Loss를 사용한다.
•
주로 사용되는 문제
◦
외래치가 존재하는 회귀 문제: 외래치가 있지만 그 영향을 너무 크게 받지 않으면서도, 작은 오차에 민감하게 반응할 때 적합하다.
◦
예를 들어, 센서 데이터나 주식 예측과 같은 분야에서 외래치가 자주 발생하지만, 예측 정확도가 중요한 경우에 Huber Loss를 사용하면 유리하다.

분류(Classification)에서의 손실함수

Cross Entropy (교차 엔트로피)

•
분류 문제에서 많이 사용되는 손실 함수
•
예측한 확률 분포와 실제 정답 확률 분포 사이의 차이를 측정
•
특히 이진 분류와 다중 클래스 분류에 사용
1.
이진 분류 (Binary Cross Entropy)
•
사용 사례: 이진 분류 문제에서 사용되는 손실함수이다. 예를 들어, 스팸 메일인지 아닌지, 고양이인지 개인지처럼 두 가지 범주로 예측하는 문제에 적합하다.
•
설명: 이진 교차 엔트로피는 예측 확률이 0 또는 1에 가까워질수록 더 낮은 손실을 가지며, 틀리게 예측할 경우 손실이 커진다. 예를 들어, 스팸 메일을 90% 확률로 스팸이라고 예측하고, 실제로 스팸이라면 손실이 작아지지만, 잘못된 예측을 하면 손실이 크게 나타난다.
•
주로 사용되는 문제:
◦
이진 분류 문제: 예를 들어, 스팸 메일 필터링이나 질병 여부 예측 등에서 사용된다.
◦
시그모이드 함수를 통해 나온 확률에 대해 사용된다.
BCE=−1n∑i=1n[yilog⁡(y^i)+(1−yi)log⁡(1−y^i)]BCE=-\frac{1}{n}\sum^n_{i=1}[y_i\log(\hat{y}_i)+(1-y_i)\log(1-\hat{y}_i)]
•
yiy_i는 실제 값(0 또는 1), y^i\hat{y}_i는 예측 값(0과 1 사이의 확률).
2.
다중 클래스 분류 (Categorical: Multi-class Cross Entropy)
•
사용 사례: 다중 클래스 분류 문제에서 각 클래스가 독립적이고, 하나의 클래스만 정답으로 나올 때 사용된다. 일반적인 교차 엔트로피와 거의 같으며, 주로 소프트맥스 함수와 함께 사용된다.
•
설명: 소프트맥스 함수는 각 클래스의 확률을 계산하고, 카테고리컬 교차 엔트로피는 모델의 예측과 실제 정답 레이블 간의 차이를 계산한다.
•
주로 사용되는 문제:
◦
이미지 분류 문제에서 한 이미지에 하나의 정답 레이블만 존재하는 경우(예: CIFAR-10, ImageNet 등).
CCE=−∑i=1nyilog⁡(y^i)CCE=-\sum^n_{i=1}y_i\log(\hat{y}_i)
•
yiy_i는 실제 클래스,y^i\hat{y}_i는 예측한 클래스의 확률

스파스 카테고리컬 교차 엔트로피(Sparse Categorical Cross-Entropy)

•
사용 목적: 다중 클래스 분류 문제에서 정수형 레이블을 사용할 때 사용되는 손실 함수이다.
•
특징
◦
정수형 레이블: 일반적인 카테고리컬 교차 엔트로피는 원-핫 인코딩된 레이블을 필요로 한다. 원-핫 인코딩은 클래스 수만큼 0과 1로 이루어진 벡터로, 정답인 클래스만 1이고 나머지는 0이다. 하지만, 스파스 카테고리컬 교차 엔트로피는 레이블이 원-핫 인코딩이 아니라, 그냥 정수형 레이블로 되어 있을 때 사용된다.
◦
예를 들어, 원-핫 인코딩된 레이블이 [0, 0, 1, 0]이라면, 스파스 카테고리컬 교차 엔트로피에서는 이 값을 그냥 정수로 2로 표현해도 된다.
•
장점
◦
메모리 효율성: 원-핫 인코딩에서는 클래스가 많을수록 벡터가 길어지지만, 스파스 카테고리컬 교차 엔트로피에서는 정수형 레이블만 사용하므로 메모리 사용량이 훨씬 적다.
◦
계산 효율성: 정수형 레이블을 바로 사용할 수 있기 때문에 계산이 더 간단해지고 효율적이다.
•
수식
Sparse Categorical Cross-Entropy=−1N∑i=1Nlog⁡(pyi)\text{Sparse Categorical Cross-Entropy} = - \frac{1}{N} \sum_{i=1}^{N} \log(p_{y_i})
◦
pyip_{y_i}는 정답 레이블yiy_i에 해당하는 예측 확률
•
사용 예
◦
다중 클래스 분류 문제에서 클래스가 많고, 각 클래스가 원-핫 인코딩을 사용하지 않고 정수형 레이블로 주어질 때 주로 사용된다.
◦
예를 들어, 이미지 분류 문제에서 각 이미지가 여러 카테고리 중 하나에 속하는 경우, 해당 이미지의 정수형 레이블을 이용해 스파스 카테고리컬 교차 엔트로피를 사용할 수 있다.

KL-발산(Kullback-Leibler Divergence, KL Divergence)

•
사용 사례: 분류 문제에서 두 확률 분포(예측 분포와 실제 분포) 사이의 차이를 측정할 때 사용된다. 주로 확률 분포를 비교할 때 사용된다.
•
설명: KL-발산은 예측한 확률 분포와 실제 확률 분포가 얼마나 다른지 측정한다. 교차 엔트로피와 유사하지만, 더 일반적인 확률 분포 사이의 차이를 계산하는 데 중점을 둔다.
•
사용 목적: 두 확률 분포 사이의 차이를 측정하는 데 사용된다. 모델의 예측 확률 분포가 실제 확률 분포와 얼마나 다른지를 계산하는 데 유용하다.
•
특징:
◦
확률 분포 간의 차이 측정: KL-발산은 두 분포가 얼마나 비슷한지 또는 다른지를 측정하는 지표다. 딥러닝에서는 주로 모델이 예측한 확률 분포와 실제 정답 분포가 얼마나 차이가 나는지 계산할 때 사용된다.
◦
예를 들어, 모델이 특정 카테고리에 대해 70% 확률로 예측했지만, 실제 정답 분포가 이와 다르다면 그 차이를 KL-발산으로 계산할 수 있다.
•
장점
◦
확률 분포 간의 차이 정밀 측정: 분포 사이의 차이를 정밀하게 측정할 수 있어서, 모델이 여러 클래스의 확률을 동시에 예측할 때 유용하다.
•
수식
DKL(P∣∣Q)=∑iP(i)log⁡(P(i)Q(i))D_{KL}(P || Q) = \sum_{i} P(i) \log \left(\frac{P(i)}{Q(i)}\right)
◦
P(i)P(i)는 실제 분포(정답 분포)이고, Q(i)Q(i)는 모델이 예측한 확률 분포다.
◦
KL-발산은 P(i)P(i)와Q(i)Q(i)가 같으면 0이 되고, 다를수록 값이 커진다.
•
사용 예
◦
변분 오토인코더(VAE): VAE에서는 인코더와 디코더 간의 잠재 공간에서의 확률 분포가 비슷해지도록 KL-발산이 사용된다.
◦
멀티 클래스 분포 비교: 여러 클래스에 대한 확률 분포를 비교하는 작업에서 자주 사용된다. 예를 들어, 자연어 처리(NLP) 모델에서 예측된 단어의 확률 분포와 실제 정답 분포를 비교할 때 사용될 수 있다.

힌지 손실(Hinge Loss)

•
사용 목적: 이진 분류 문제에서, 특히 서포트 벡터 머신(SVM)에서 주로 사용되는 손실 함수이다. 모델이 예측한 값이 정답을 충분히 구분할 수 있는지 확인하는 역할을 한다.
•
설명: 이진 분류에서 정답과 예측값의 차이를 계산하며, 분류 결과가 경계(margin)를 넘어서면 손실이 발생하지 않고, 그렇지 않으면 손실이 발생한다.
•
특징:
◦
마진 기반 손실: 힌지 손실은 예측 값이 실제 값과 어느 정도 차이가 있어야 하는지를 나타내는 마진(margin)을 설정한다. 이 마진을 넘지 않으면 손실이 발생하며, 마진을 넘으면 손실이 발생하지 않는다.
◦
예를 들어, 예측 값이 1이어야 할 때 모델이 0.8을 예측하면 여전히 손실이 발생하지만, 1.2를 예측하면 손실이 발생하지 않는다. 즉, 정답을 확실하게 예측하도록 유도한다.
•
장점
◦
이진 분류 문제에서 경계 구분 강화: SVM처럼 분류 경계를 확실하게 구분하는 문제에 적합하며, 예측이 모호한 경우에는 큰 손실을 주어 모델을 더 명확하게 학습시킨다.
•
수식
Hinge Loss=max⁡(0,1−yi⋅y^i)\text{Hinge Loss} = \max(0, 1 - y_i \cdot \hat{y}_i)
◦
여기서 yiy_i는 실제 레이블(1 또는 -1), y^i \hat{y}_i는 모델의 예측 값이다.
◦
만약 모델이 정확하게 예측했다면 손실은 0이 되고, 그렇지 않으면 손실이 발생한다.
•
사용 예:
◦
서포트 벡터 머신(SVM): 힌지 손실은 SVM에서 자주 사용된다. SVM은 두 클래스 사이에 최대 마진을 확보하면서 분류를 수행하는 모델이기 때문에, 힌지 손실을 사용하여 그 마진을 강화한다.
◦
이진 분류 문제: 0과 1 또는 -1과 1로 이루어진 이진 분류 문제에서 사용되며, 예를 들어 이미지 분류에서 고양이와 개를 구분하는 문제에 적합하다.

손실 함수의 선택

•
회귀 문제
◦
MAE: 오차의 절대값을 평균하여 계산. 외래치에 덜 민감하고, 각 오차에 대해 균등하게 반영되므로 외래치가 적은 회귀 문제에 적합.
◦
MSE: 오차를 제곱한 후 평균하여 계산. 큰 오차에 더 큰 패널티를 주는 방식으로 외래치에 민감한 문제에 적합.
◦
Huber Loss: 외래치가 존재하는 회귀 문제 - 외래치가 있지만 그 영향을 너무 크게 받지 않으면서도, 작은 오차에 민감하게 반응할 때 적합
•
분류 문제
◦
이진 교차 엔트로피: 이진 분류 문제에서 사용.
◦
카테고리컬 교차 엔트로피: 다중 클래스 분류에서 원-핫 인코딩된 레이블을 사용할 때 적합.
◦
스파스 카테고리컬 교차 엔트로피: 다중 클래스 분류에서 정수형 레이블을 사용할 때 사용.
◦
KL-발산: 두 확률 분포 간의 차이를 측정하는 데 사용.
◦
힌지 손실: 주로 SVM과 같은 모델에서 사용.

경사하강법(Gradient Descent)

•
모델이 잘 학습할수 있도록 기울기(변화율)을 사용하여 모델의 파라미터를 조정하는 방법
•
손실 함수(Loss Function)를 최소화하기 위해 사용되는 최적화 알고리즘
◦
손실 함수의 기울기(그래디언트: Gradient)를 따라 내려가면서 최적의 값을 찾는 방식
기울기(Gradient): 손실 함수의 각 파라미터에 대한 편미분 값 기울기는 현재 위치에서 손실 함수가 가장 빠르게 증가하는 방향을 지침. 경사 하강법은 이 기울기의 반대 방향으로 이동하여 손실 값을 줄인다.
•
수식
θ:=θ−η⋅∇θLθ:=θ−η⋅∇_θL
◦
θθ: 모델의 파라미터(가중치 및 편향)
◦
η\eta: 학습률 (Learning Rate)
◦
∇θL\nabla_\theta L: 손실 함수 L에 대한 파라미터 θ의 기울기(그래디언트)
•
목표는 모델의 예측 값과 실제 값 사이의 오차(손실)를 줄이는 방향으로 가중치(Weight)와 편향(Bias)을 업데이트하는 것
1.
예측과 실제값을 비교하여 손실을 구한다.
2.
손실이 작아지는 방향으로 파라미터를 수정한다.
3.
이과정을 반복한다.
◦
경사(기울기): 파라미터에 대한 오차의 변화
▪
기울기 + : 파라미터 ↓
▪
기울기 - : 파라미터 ↑

학습률(Learning Rate)

•
파라미터를 업데이트하는 정도를 조절하기 위한 값
•
각 업데이트 단계에서 파라미터가 이동하는 크기를 결정하는 값
•
학습률이 너무 크면 손실 함수의 최솟값을 놓칠 수 있고, 너무 작으면 학습 속도가 느려짐

학습률이 너무 큰경우

학습률이 너무 작을 경우

경사 하강법의 유형

1.
배치 경사 하강법 (Batch Gradient Descent)
•
설명: 전체 데이터셋을 사용하여 한 번에 한 단계씩 가중치를 업데이트합니다. 데이터셋이 클수록 계산 비용이 많이 들 수 있지만, 매번 정확한 기울기를 계산합니다.
•
장점: 매우 안정적이고, 매번 정확한 경사도를 계산함.
•
단점: 데이터셋이 클 때 계산량이 매우 커져서 학습 속도가 느릴 수 있음.
2.
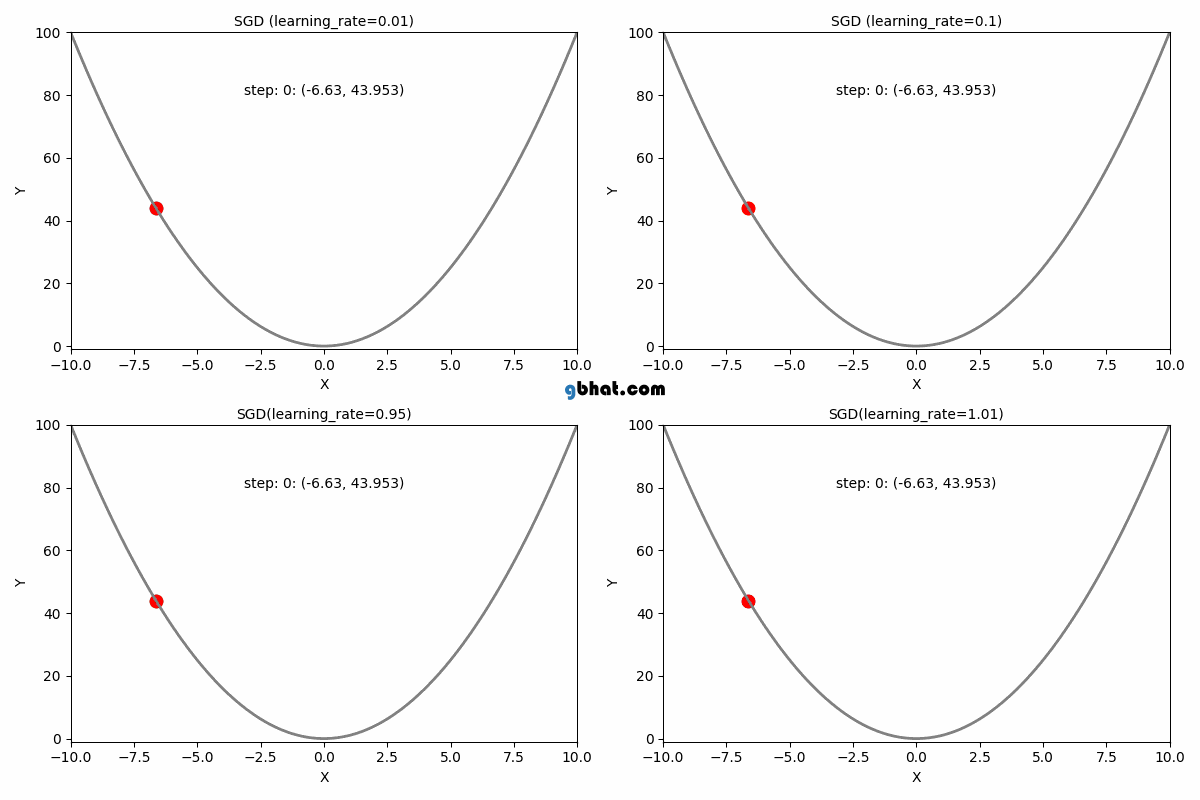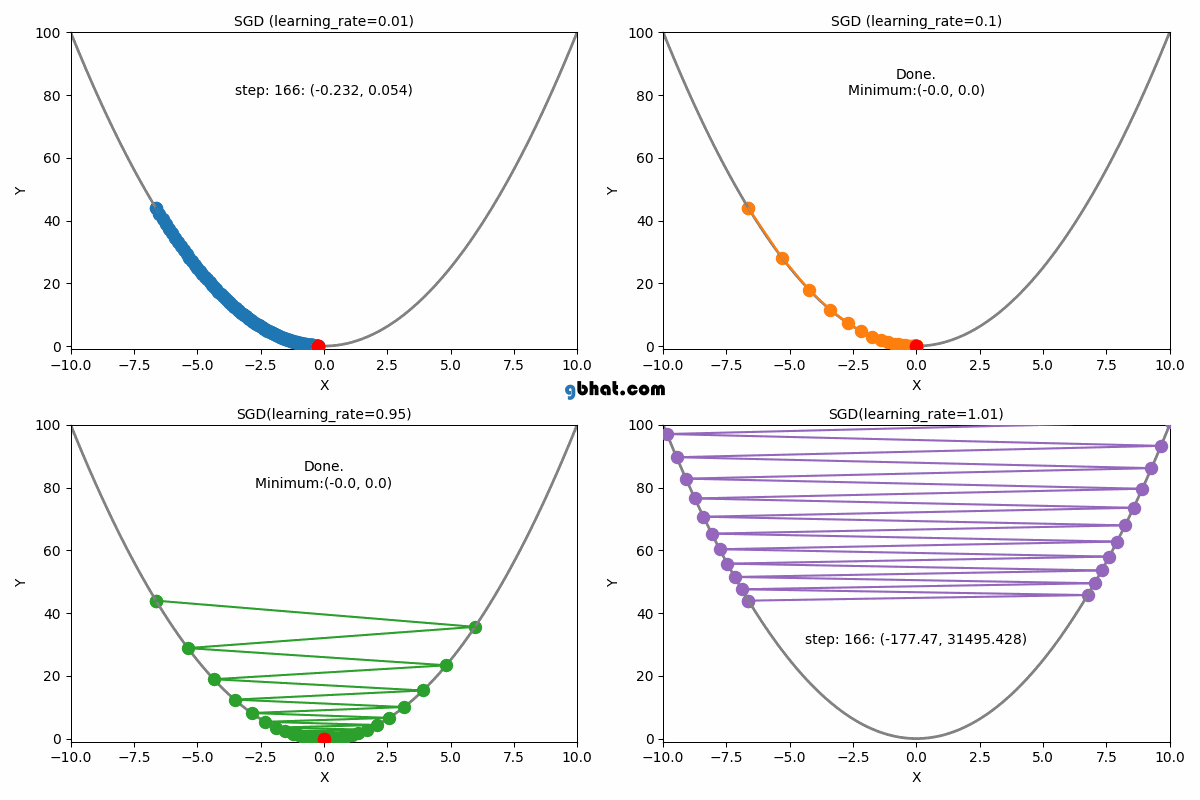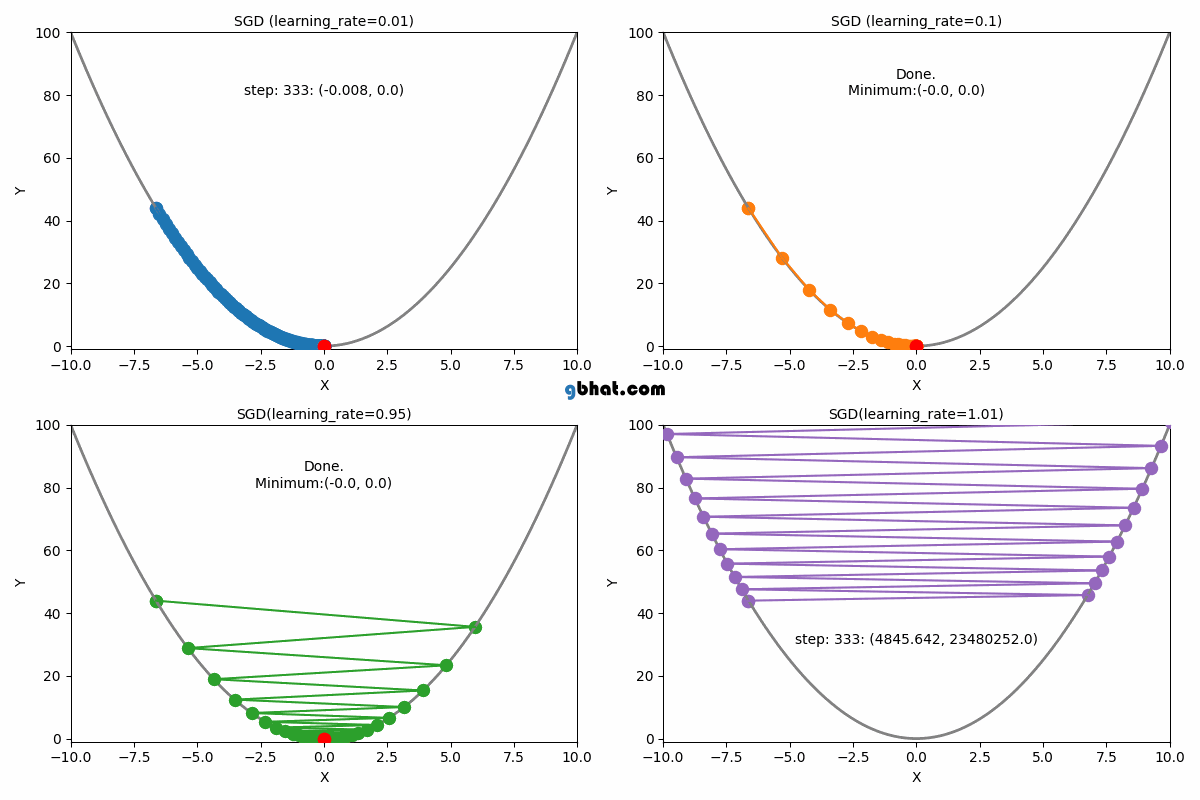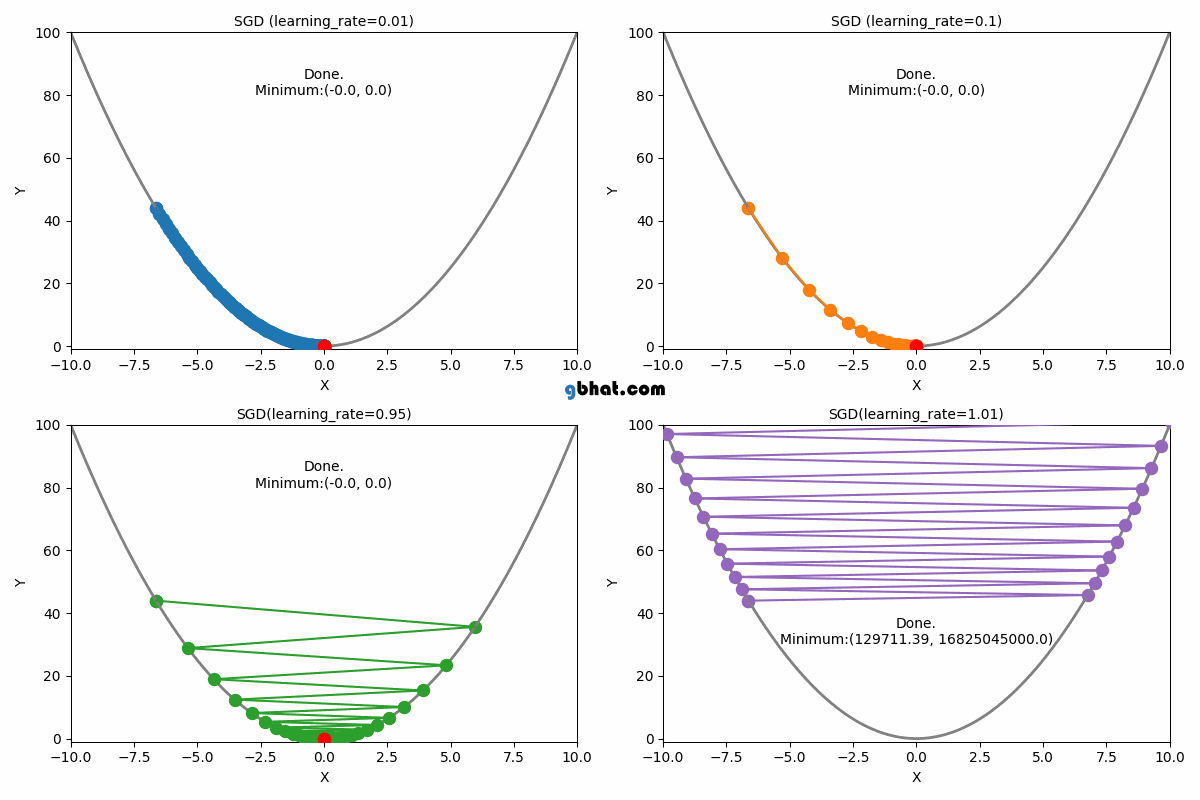
확률적 경사 하강법 (Stochastic Gradient Descent, SGD)
•
설명: 전체 데이터셋 대신 하나의 샘플에 대해 기울기를 계산하고, 그에 따라 가중치를 업데이트합니다. 따라서 각 업데이트가 매우 빠르게 이루어집니다.
•
장점: 빠르고, 큰 데이터셋에서 유용함.
•
단점: 경로가 불안정하고 진동할 수 있어, 손실 함수의 최솟값 근처에서 오차가 크게 발생할 수 있음.
3.
미니배치 경사 하강법 (Mini-batch Gradient Descent)
•
설명: 데이터셋을 작은 배치로 나누어 각 배치에 대해 기울기를 계산하고 가중치를 업데이트합니다. 배치 경사 하강법과 확률적 경사 하강법의 절충 방식입니다.
•
장점: 계산 효율성과 안정성을 동시에 추구함.
•
단점: 배치 크기를 잘못 설정하면 학습 속도가 느리거나 불안정해질 수 있음.

경사 하강법의 문제점과 해결 방법

1.
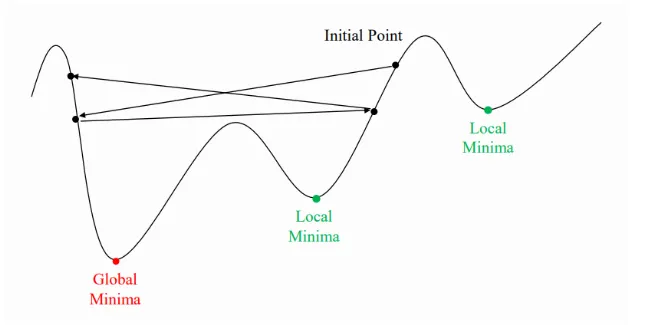
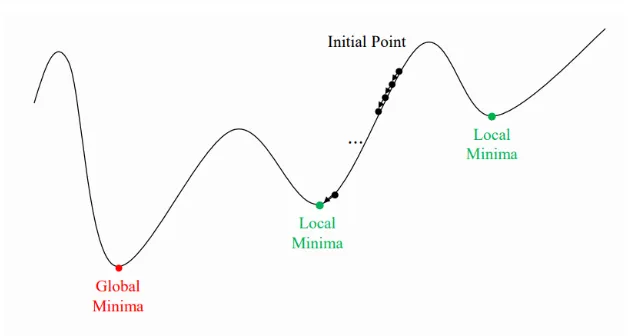
지역 최솟값(Local Minimum)
•
손실 함수가 여러 최솟값을 가질 수 있는데, 경사 하강법은 가장 낮은 점(global minimum) 대신 특정 지역에서의 최솟값(local minimum)에 도달할 수 있다.
•
다만, 실제 딥러닝 모델의 손실 함수는 고차원 공간에서 매우 복잡해 "안장점(saddle point)"에 빠지는 경우가 더 흔하다.
2.
학습률(Learning Rate) 문제:
•
학습률이 너무 크면 모델이 손실 함수의 최솟값을 지나치게 되어 수렴하지 않을 수 있다.
•
학습률이 너무 작으면 학습이 매우 느리게 진행된다.
•
해결 방법: 학습률을 점진적으로 줄이는 방법인 학습률 스케줄링이나 적응형 학습률(Adam, RMSProp 등) 알고리즘을 사용할 수 있다.
3.
느린 수렴
•
경사 하강법은 손실 함수의 기울기가 거의 0인 평탄한 구간에서는 학습 속도가 매우 느려질 수 있다.
•
해결 방법: 모멘텀(Momentum) 같은 기법을 사용하여 이전 기울기를 참고해 수렴 속도를 높일 수 있다.

역전파(Back-propagation)

•
가중치(Weight)와 편향(Bias)을 학습시키기 위한 핵심 알고리즘
•
역전파는 모델의 예측 값과 실제 값 사이의 오차(손실)를 계산한 후, 이 오차를 기울기(Gradient)를 이용해 각 가중치에 어떻게 반영해야 하는지 결정
•
이를 통해 모델의 성능을 개선하는 방향으로 가중치를 업데이트
•
효율적인 계산을 위해 역전파 알고리즘을 사용
◦
손실값을 구해 이 손실에 관여하는 가중치들을 손실이 작아지는 방향으로 수정하는 알고리즘
•
파라미터를 업데이트할때 필요한 손실에 대한 기울기를 역방향으로 업데이트

핵심 개념

•
연쇄 법칙 (Chain Rule)
◦
역전파는 연쇄 법칙을 사용해 각 가중치에 대한 손실 함수의 기울기를 계산한다.
◦
예를 들어, 두 개의 함수 f(x)f(x)와 g(x)g(x)가 연쇄적으로 적용되는 경우,
◦
이 함수의 합성함수 h(x)=f(g(x))h(x)=f(g(x))에 대한 미분은 다음과 같다
dhdx=dfdg⋅dgdx\frac{dh}{dx}=\frac{df}{dg}⋅\frac{dg}{dx}
•
오차 전파
◦
역전파는 출력 층에서부터 시작하여 이전 층으로 거슬러 올라가면서 오차를 전파한다.
◦
각 층의 가중치에 대해 오차가 어떻게 영향을 미치는지를 계산한 후, 이 정보를 이용해 가중치를 조정한다.
•
가중치와 편향 업데이트
◦
역전파를 통해 계산된 기울기는 경사 하강법을 통해 가중치와 편향을 업데이트하는 데 사용된다.
◦
이를 반복하여 모델의 성능을 점진적으로 개선한다.

동작 원리

•
역전파는 기본적으로 연쇄 법칙(Chain Rule)을 이용해, 네트워크의 출력에서부터 입력으로 거꾸로 기울기(Gradient)를 전파하면서 각 층의 가중치에 대한 오차의 기울기를 계산
•
그 후, 이 기울기를 사용해 가중치를 업데이트

주요 단계

1.
순전파(Forward Propagation)
•
입력 데이터가 신경망을 통과하며 각 층에서 계산이 이루어진다.
•
각 층의 출력은 다음 층의 입력으로 전달되며, 마지막 층에서 최종 출력이 계산된다.
•
최종 출력과 실제 값 사이의 손실(Loss)이 계산된다.
2.
손실 계산
•
손실 함수(예: MSE, Cross Entropy)를 사용해 모델이 예측한 출력 값과 실제 값 간의 오차를 계산.
3.
역전파(Backpropagation)
•
계산된 손실을 기준으로, 출력에서 입력 방향으로 기울기를 계산. 이는 연쇄 법칙을 사용해 각 가중치에 대한 기울기를 구하는 과정.
•
각 층에서, 손실 함수에 대한 각 가중치의 편미분을 계산.
4.
가중치 업데이트
•
경사 하강법(Gradient Descent) 또는 Adam과 같은 최적화 알고리즘을 사용해, 계산된 기울기를 기반으로 가중치를 업데이트.
θ:=θ−η⋅∇θLθ:=θ−η⋅∇_θL
◦
θ: 가중치
◦
η\eta: 학습률(Learning Rate)
◦
∇θL\nabla_\theta L: 손실 함수 L에 대한 가중치 θ의 기울기

기울기 소실 문제와 활성화 함수

•
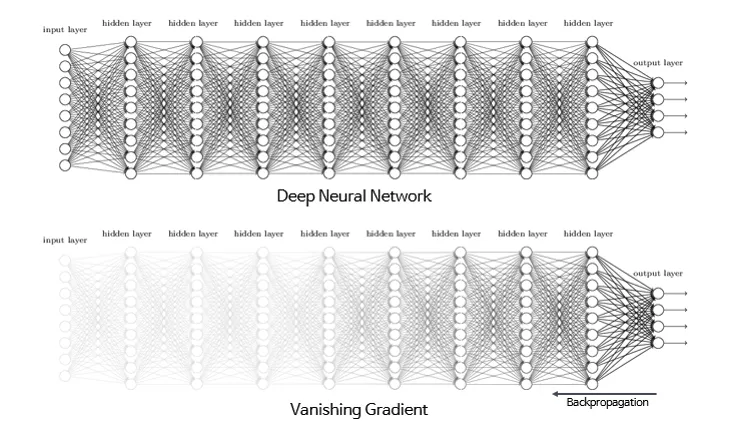
층이 깊어지면서 역전파과정에서 가중치를 수정하려는 기울기가 중간에 0이 되어버리거나 0에 매우 가깝게 작아지는 경사 소실(vanishing gradient) 문제가 발생

기울기 소실(Vanishing Gradient) - 역전파의 한계

•
딥러닝이 복잡해질 수록 기울기 소실이 발생
•
기울기 소실 원인은 활성화 함수(Activation Function)의 기울기와 관련이 깊다.
•
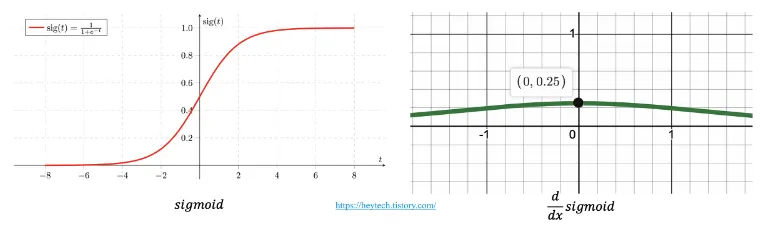
아래 활성화 함수 중 하나인 Sigmoid 함수를 보자
•
x값이 크거나 작아짐에 따라 기울기가 거의 0에 수렴하고 있다. 즉, Sigmoid 함수를 사용한 복잡한 딥러닝 모델은 학습이 제대로 이루어지지 않게 된다.
•
기울기 소실 문제는 주로 시그모이드(Sigmoid)나 탠H(Tanh)와 같은 비선형 활성화 함수에서 발생
•
입력층이나 중간층의 가중치가 거의 업데이트되지 않아 모델이 효과적으로 학습하지 못하게 된다.
•
이러한 함수들은 출력이 0에 가까울 때 기울기 값이 매우 작아지기 때문에, 역전파를 통해 기울기를 전파할 때 그 값이 점점 작아져 결국에는 거의 0이 된다.
•
여러 층을 거치면 기울기가 급격히 감소하여 학습이 잘 이루어지지 않는다.
시그모이드 함수: 시그모이드 함수의 출력은 0과 1 사이의 값이며, 입력이 크거나 작을수록 기울기는 0에 가까워진다.
σ(x)=11+e−x,dσdx=σ(x)(1−σ(x))\sigma(x) = \frac{1}{1 + e^{-x}}, \\ \frac{d\sigma}{dx} = \sigma(x)(1 - \sigma(x))
탠H 함수: 탠H 함수는 출력이 -1에서 1 사이이며, 이 함수 역시 입력이 커질수록 기울기가 0에 가까워진다.
tanh⁡(x)=ex−e−xex+e−x,dtanh⁡dx=1−tanh⁡(x)2\tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}, \\ \frac{d\tanh}{dx} = 1 - \tanh(x)^2

기울기 소실 예시

•
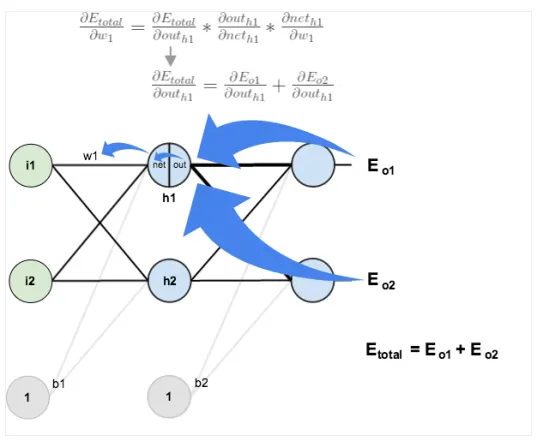
z1, z2, z3는 각 layer의 node의 출력과 가중치의 합성곱이다.
•
h1(hidden1), h2(hidden2), h3(hidden3)는 z1, z2, z3값의 활성함수, sigmoid 함수의 결과이다.(결과이자 각 노드의 출력이다.)
•
끝의 상자 J는 시스템의 에러를 집계하여 반환한다.(손실함수,loss function)
•
그런 다음 J의 출력 이 최소화 되도록 경사 하강법(gradient descent)을 통해 weight를 업데이트 하기 위해 Backpropagation을 수행한다.
◦
가중치 w1에 대해 미분하려면 연쇄법칙(chain rule)에 따라 다음과 같이 미분이 된다.
∂error∂w1=∂error∂output∗∂output∂hidden2∗∂hidden2∂hidden1∗∂hidden1∂w1\frac{\partial error}{\partial w_1} = \frac{\partial error}{\partial output} * \frac{\partial output}{\partial hidden2} * \frac{\partial hidden2}{\partial hidden1} * \frac{\partial hidden1}{\partial w_1}
◦
여기서 하단 공식을 자세히 살펴보면
∂output∂hidden2∗∂hidden2∂hidden1\frac{\partial output}{\partial hidden2} * \frac{\partial hidden2}{\partial hidden1}
◦
z1=hidden2∗w3z1=hidden2∗w3이고, output=sigmoid(z1)output=sigmoid(z1)이므로, 다음 수식처럼 나타낼 수 있다.
∂output∂hidden2=∂z1∂hidden2∗∂output∂z1\frac{\partial output}{\partial hidden2} = \frac{\partial z_1}{\partial hidden2} * \frac{\partial output}{\partial z_1}
◦
마찬가지로, 해당 수식도
∂output∂hidden2=∂sigmoid(z1)∂z1∗w3\frac{\partial output}{\partial hidden2} = \frac{\partial sigmoid(z_1)}{\partial z_1} * w_3
◦
z2=hidden1∗w2z2=hidden1∗w2이고, hidden2=sigmoid(z2)hidden2=sigmoid(z2)이므로, 다음 수식처럼 나타낼 수 있다.
∂hidden2∂hidden1=∂z2∂hidden1∗∂hidden2∂z2\frac{\partial hidden2}{\partial hidden1} = \frac{\partial z_2}{\partial hidden1} * \frac{\partial hidden2}{\partial z_2}
◦
따라서, 결론적으로 다음 수식처럼 나타낼 수 있다.
∂output∂hidden2∗∂hidden2∂hidden1=∂sigmoid(z1)∂z1∗w3∗∂sigmoid(z2)∂z2∗w2\frac{\partial output}{\partial hidden2} * \frac{\partial hidden2}{\partial hidden1} = \frac{\partial sigmoid(z_1)}{\partial z_1} * w_3 * \frac{\partial sigmoid(z_2)}{\partial z_2} * w_2
▪
layer가 진행될 수록 sigmoid 함수가 연속으로 곱해지는 것을 알 수 있다.
▪
sigmoid 함수의 미분은 0 ~ 0.25로 1보다 작으므로 곱해지는 횟수가 많을 수록 값은 점점 더 작아진다.
▪
즉 layer가 많을 수록 기울기의 값은 더 작아진다.
▪
이를 해결하기 위해 나온 활성함수가 바로 ReLU(Rectified Linear Unit)이다.

기울기 손실 해결방법 - 활성화 함수

•
아래 그림과 같이 ReLU는 Simoid와는 다르게 기울기 소실 문제를 해결할 수 있다.
•
또한 수식이 단순하여 연산 속도 또한 빠르다는 장점이 있다.

활성화 함수 종류

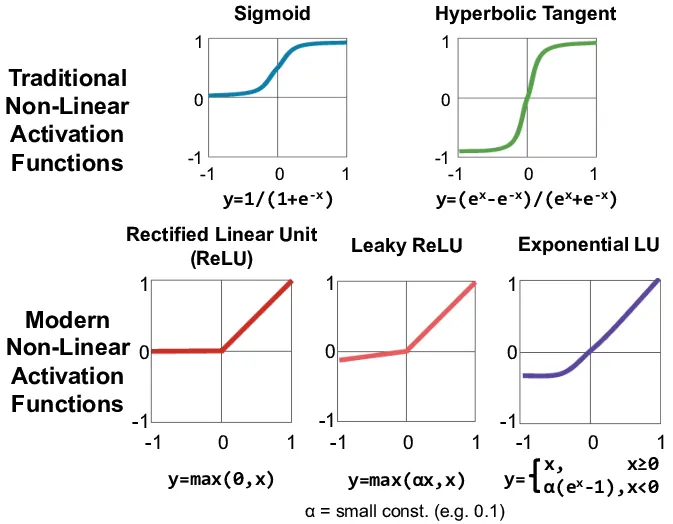
Sigmoid 함수

•
그래프: 입력 값이 클수록 1에 가까워지고, 작을수록 0에 가까워진다.
•
특징: 기울기가 입력 값이 클 때나 작을 때 0에 가까워지기 때문에 기울기 소실 문제가 발생

Tanh 함수

•
그래프: 입력이 클 때는 1에, 작을 때는 -1에 가까워진다.
•
특징: Sigmoid 함수와 유사하게 기울기가 0에 가까워져서 깊은 네트워크에서 기울기 소실이 발생

ReLU 함수

•
그래프: 입력이 양수일 때는 그대로 출력되고, 음수일 때는 0이 됩니다.
•
특징: 기울기가 0 또는 1이기 때문에 기울기 소실 문제를 완화할 수 있다. 그러나 음수 입력에 대해서는 기울기가 0이 되는 죽은 ReLU 문제가 있을 수 있다.

Leaky ReLU 함수

•
그래프: 입력이 음수일 때에도 작은 기울기(0.01)를 유지
•
특징: ReLU 함수의 단점을 보완하여, 음수 구간에서도 작은 기울기를 제공함으로써 죽은 ReLU 문제를 해결

ELU 함수

•
그래프: 입력이 양수일 때는 그대로 출력되고, 음수일 때는 지수적으로 감소
•
특징: 음수 구간에서 기울기가 0으로 소실되지 않아 기울기 소실 문제를 해결할 수 있다. 하지만 계산 복잡도가 ReLU보다 높을 수 있다.

배치(Batch)

•
배치의 사전적 의미는 (일괄적으로 처리되는) 집단
•
배치는 한번에 여러개의 데이터를 묶어서 입력하는 것인데, GPU의 병렬 연산 기능을 취대한 효율적으로 사용하기 위해 쓴 방법이다.
•
전체 데이터셋을 한 번에 학습하기에는 메모리나 시간적인 제약이 있을 수 있기 때문에, 데이터를 여러 개의 작은 배치로 나누어 처리한다.
•
각 배치에는 여러 개의 데이터 샘플이 포함되어 있으며, 모델은 이 배치를 사용해 가중치를 업데이트한다.

핵심 개념

•
배치 크기(Batch Size)
◦
한 번에 모델에 입력되는 데이터 샘플의 개수
◦
예를 들어, 배치 크기가 32라면, 한 번의 학습에서 32개의 샘플이 사용
◦
배치 크기가 클수록 메모리 사용량이 증가하지만, 업데이트 횟수가 줄어든다.
•
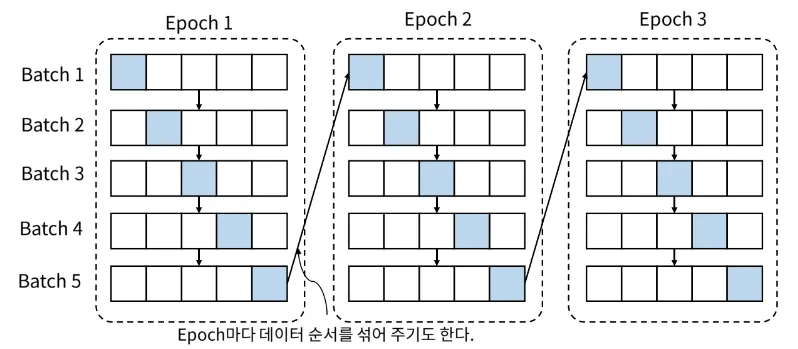
에포크(Epoch)
◦
전체 데이터셋을 한 번 모두 학습하는 과정을 한 에포크라고 지칭
◦
예를 들어, 데이터셋이 1000개고 배치 크기가 100이면, 한 에포크는 10번의 배치 업데이트로 이루어진다.
Epoch:학습 데이터 전체를 한 번 학습하는 단위 Batch: 기울기(Gradient)를 구하는 단위

배치의 종류

•
전체 배치 (Full Batch, Batch Gradient Descent)
◦
전체 데이터셋을 한 번에 학습시키는 방식
◦
각 에포크마다 가중치를 한 번만 업데이트
◦
장점: 전체 데이터에 대해 error gradient를 계산하기 때문에 optimal로 수렴이 안정적이다.
◦
단점: local optimal 상태가 되면 빠져나오기 힘듦, 데이터셋이 크면 메모리 소모가 매우 크다
•
확률적 경사 하강법 (Stochastic Gradient Descent, SGD)
◦
각 데이터 샘플을 하나씩 학습시키는 방식
◦
빠르지만, 기울기가 불안정하고 최솟값 근처에서 진동할 수 있다.
◦
장점: 아래 이미지에서 보이듯이 shooting이 일어나기 때문에 local optimal에 빠질 위험이 적다.
◦
단점: global optimal을 찾지 못 할 가능성이 있다.
•
미니배치(Mini-Batch Gradient Descent)
◦
데이터를 여러 개의 작은 배치로 나누어 학습시키는 방식.
◦
가장 많이 사용되는 방식이다.
◦
메모리 효율성이 좋고, 학습 속도와 안정성의 균형을 맞춘다.
◦
장점: BGD(Batch Gradient Descent)보다 local optimal에 빠질 리스크가 적다.
◦
단점: batch size(mini-batch size)를 설정해야 한다.

Gradient Descent 방법

•
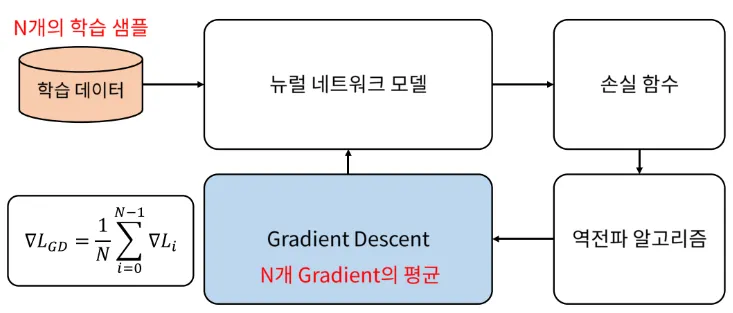
아래와 같이 일반적인 gradient descent에서는 gradient를 한번 업데이트 하기 위하여 모든 학습 데이터를 사용한다.
•
즉, 학습 데이터 전부를 넣어서 gradient를 다 구하고 그 모든 gradient를 평균해서 한번에 모델 업데이트를 합니다.
•
이런 방식으로 하면 대용량의 데이터를 한번에 처리하지 못하기 때문에 데이터를 batch 단위로 나눠서 학습을 하는 방법을 사용하는 것이 일반적입니다.

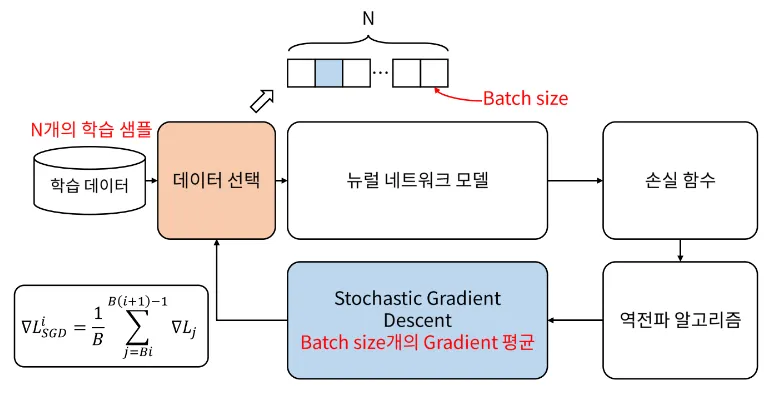
SGD(Stochastic Gradient Descent) 방법

•
SGD에서는 gradient를 한번 업데이트 하기 위하여 일부의 데이터만을 사용
•
즉, batch size 만큼만 사용하는 것
•
아래 gradient descent의 식을 보면 ∑에 i=Bii=B_i가 있는데, B가 batch의 크기가 된다.
•
한번 업데이트 하는 데 B개의 데이터를 사용하였기 때문에 평균을 낼 때에도 B로 나누어 주고 있다.

에포크(Epoch)

•
전체 데이터셋을 한 번 모두 학습시키는 과정

에포크의 역할

1.
모델 성능 개선
•
에포크가 진행될수록 모델이 데이터를 학습하면서 성능이 향상된다.
•
각 에포크마다 모델의 가중치가 업데이트되고, 모델은 입력 데이터와 목표 값 사이의 관계를 점점 더 잘 파악하게 된다.
2.
과적합(Overfitting) 위험
•
에포크 수가 너무 많으면 모델이 학습 데이터를 과하게 학습하는 과적합이 발생할 수 있다.
•
즉, 훈련 데이터에 너무 맞추어져서 새로운 데이터에 대한 일반화 성능이 떨어질 수 있다.
3.
조기 종료(Early Stopping)
•
학습이 너무 많이 진행되어 과적합이 발생하는 것을 막기 위해 조기 종료 기법을 사용한다.
•
에포크 수가 너무 많으면 손실이 더 이상 줄어들지 않거나 검증 성능이 떨어지기 시작하는 지점을 찾아 학습을 중단한다.

에포크와 손실 함수 관계

•
모델이 학습하는 동안, 각 에포크가 끝날 때마다 손실 함수(Loss Function)를 계산하여 모델의 성능을 평가한다.
•
일반적으로 초기에는 손실이 감소하다가, 어느 순간부터는 더 이상 개선되지 않거나 오히려 손실이 증가하는 경우도 있다.
•
이 지점에서 학습을 멈추거나 에포크 수를 조정한다.

에포크와 배치의 관계

•
배치(Batch)
◦
에포크 동안 학습 데이터를 여러 개의 배치로 나누어 학습한다.
◦
배치 크기(Batch Size)가 32이고 데이터셋에 3200개의 샘플이 있다면, 1 에포크 동안 100번의 배치 업데이트가 이루어진다.
•
에포크(Epoch): 모델이 데이터셋 전체를 한 번 학습할 때마다 1 에포크가 완료된다. 따라서 여러 에포크가 반복되면, 모델은 데이터셋을 여러 번 학습하게 된다.

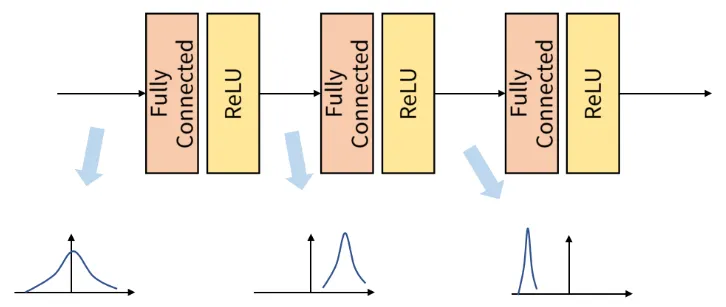
입력의 데이터 분포가 달라지는 현상(Internal Covariant Shift)

•
딥러닝 모델의 학습 과정에서 각 층의 입력 데이터 분포가 학습 도중 계속 변화하는 현상
•
Batch 단위로 학습을 하게 되면 아래 이미지와 같이 학습 과정에서 계층 별로 입력의 데이터 분포가 달라지는 현상이 발생하는데, 이것을 Internal Covariant Shift라고 한다.
•
Covariate Shift는 원래 머신러닝에서 훈련 데이터와 테스트 데이터의 분포가 서로 달라지는 현상을 의미 → Internal Covariate Shift는 이 개념을 신경망의 각 층에서 적용한 것
•
신경망의 여러 층을 통과하면서, 가중치와 편향이 학습될 때마다 각 층의 입력 분포가 변화
→ 초반에 설정된 입력 분포와 학습이 진행되면서 각 층에 전달되는 입력 분포가 달라지는 현상
•
각 계층에서 입력으로 feature를 받게 되고 그 feature는 convolution이나 fully connected 연산을 거친 뒤 activation function을 적용하게 된다.
•
그러면 연산 전/후에 데이터 간 분포가 달라질 수가 있다.
•
이와 유사하게 Batch 단위로 학습을 하게 되면 Batch 단위간에 데이터 분포의 차이가 발생할 수 있다.
•
이 문제를 개선하기 위한 개념이 배치 정규화(Batch Normalization)이다.

Internal Covariate Shift의 문제점

1.
학습 속도 저하: 각 층의 입력 분포가 계속 변하면, 신경망이 학습을 안정적으로 진행하기 어렵습니다. 매번 변화하는 입력에 맞추어 가중치가 다시 조정되어야 하므로, 학습 속도가 느려질 수 있습니다.
2.
초기화 민감도: 입력 데이터의 분포가 자주 바뀌면, 모델은 적절한 가중치 초기화에 매우 민감해질 수 있습니다. 잘못된 초기화는 학습을 불안정하게 만들 수 있습니다.
3.
기울기 소실 문제: 입력 분포의 변화로 인해 역전파 과정에서 기울기가 불안정하게 전파되거나, 기울기 소실(Gradient Vanishing)과 같은 문제를 야기할 수 있습니다.

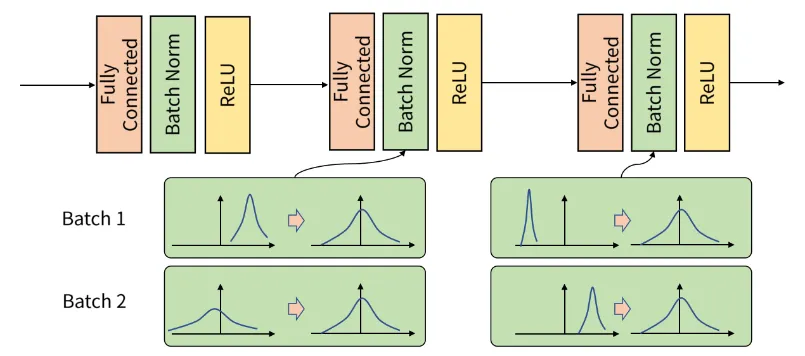
배치 정규화(Batch Normalization)

•
학습 과정에서 각 배치 단위 별로 데이터가 다양한 분포를 가지더라도 각 배치별로 평균과 분산을 이용해 정규화하는 것
x^(k)=x(k)−μBσB2+ϵ\hat{x}^{(k)} = \frac{x^{(k)} - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}}
◦
x(k)x^{(k)}는 정규화된 출력
◦
μB\mu_B는 미니배치에서의 평균
◦
σB2\sigma_B^2는 미니배치에서의 분산
◦
ϵ\epsilon은 0으로 나누는 것을 방지하기 위한 작은 값
•
아래 그림을 보면 batch 단위나 layer에 따라서 입력 값의 분포가 모두 다르지만 정규화를 통하여 분포를 zero mean gaussian 형태로 만든다.
•
그러면 평균은 0, 표준편차는 1로 데이터의 분포를 조정할 수 있다.

최적화 알고리즘(Optimizer)

•
미니배치 경사하강법의 방식을 보완하고, 학습 속도를 높이기위한 알고리즘
•
딥러닝 및 머신러닝에서 모델의 가중치와 편향을 학습시키는 데 사용되는 알고리즘
•
모델이 예측한 값과 실제 값 사이의 오차(손실)를 최소화하는 방향으로 가중치와 편향을 업데이트
•
손실 함수(Loss Function)와 결합되어, 모델이 더 정확한 예측을 할 수 있도록 학습 과정을 조절

Optimizer의 역할

1.
손실 함수 최소화
•
모델이 예측한 결과와 실제 값 간의 차이를 나타내는 손실 함수를 최소화하는 것이 목표
•
Optimizer는 이 손실 함수의 기울기(Gradient)를 계산하여 가중치를 업데이트하는 방향을 결정
2.
가중치 및 편향 업데이트
•
Optimizer는 손실 함수의 기울기를 기반으로, 모델의 가중치와 편향을 학습률에 맞추어 업데이트한다.
3.
학습률(Learning Rate)
•
옵티마이저(Optimizer)는 학습률을 고려하여 얼마나 빠르게 가중치를 업데이트할지를 결정
•
학습률이 너무 크면 최적값을 지나칠 수 있고, 너무 작으면 학습 속도가 느려질 수 있다.

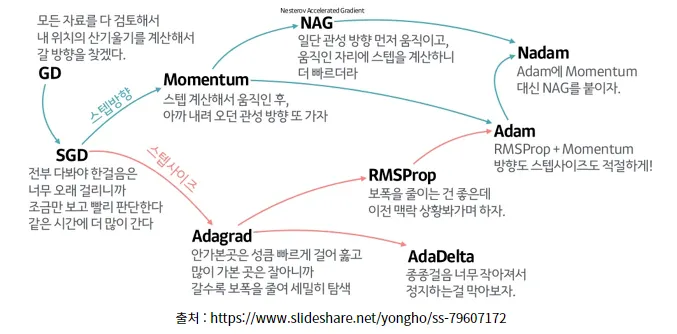
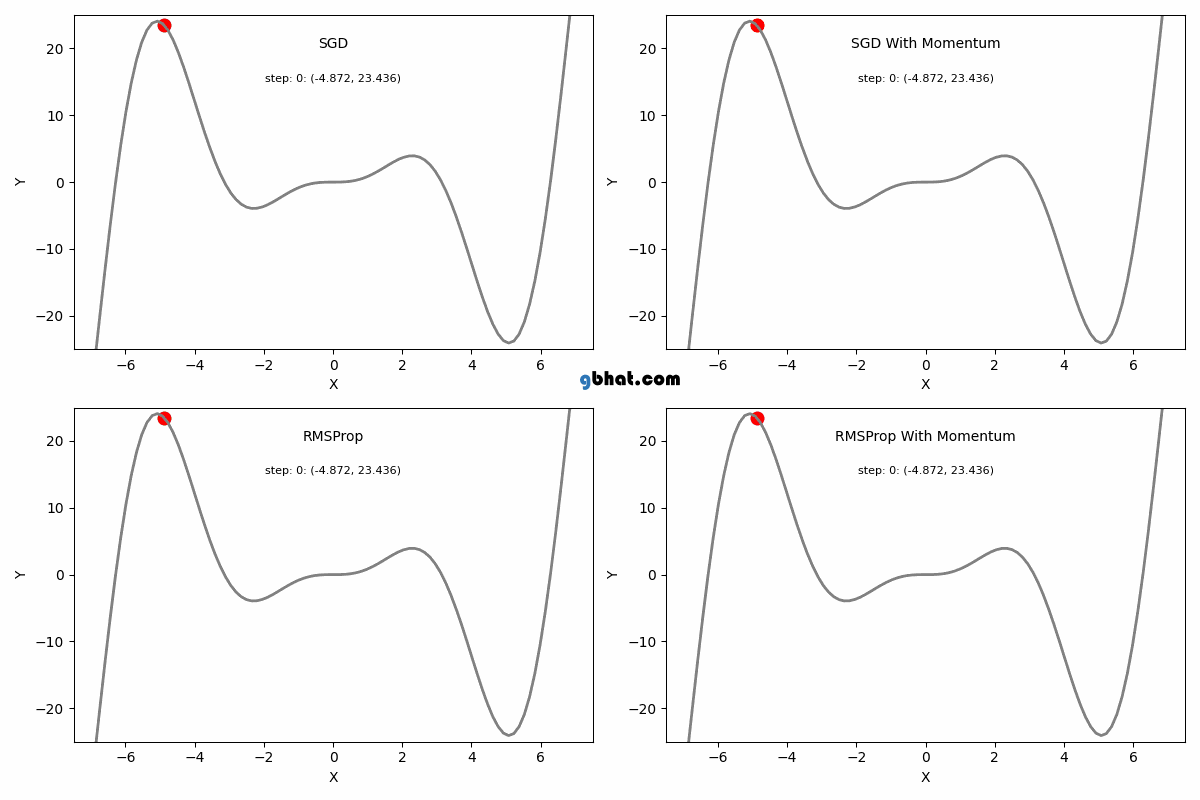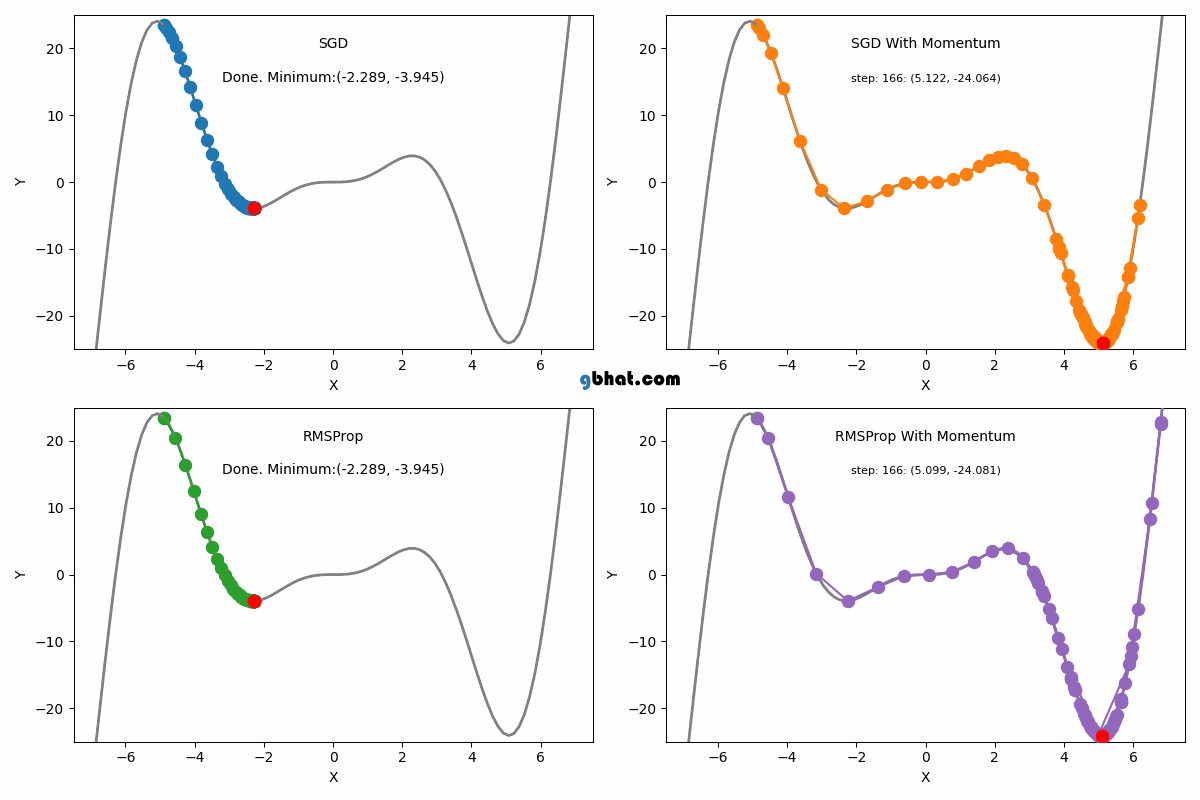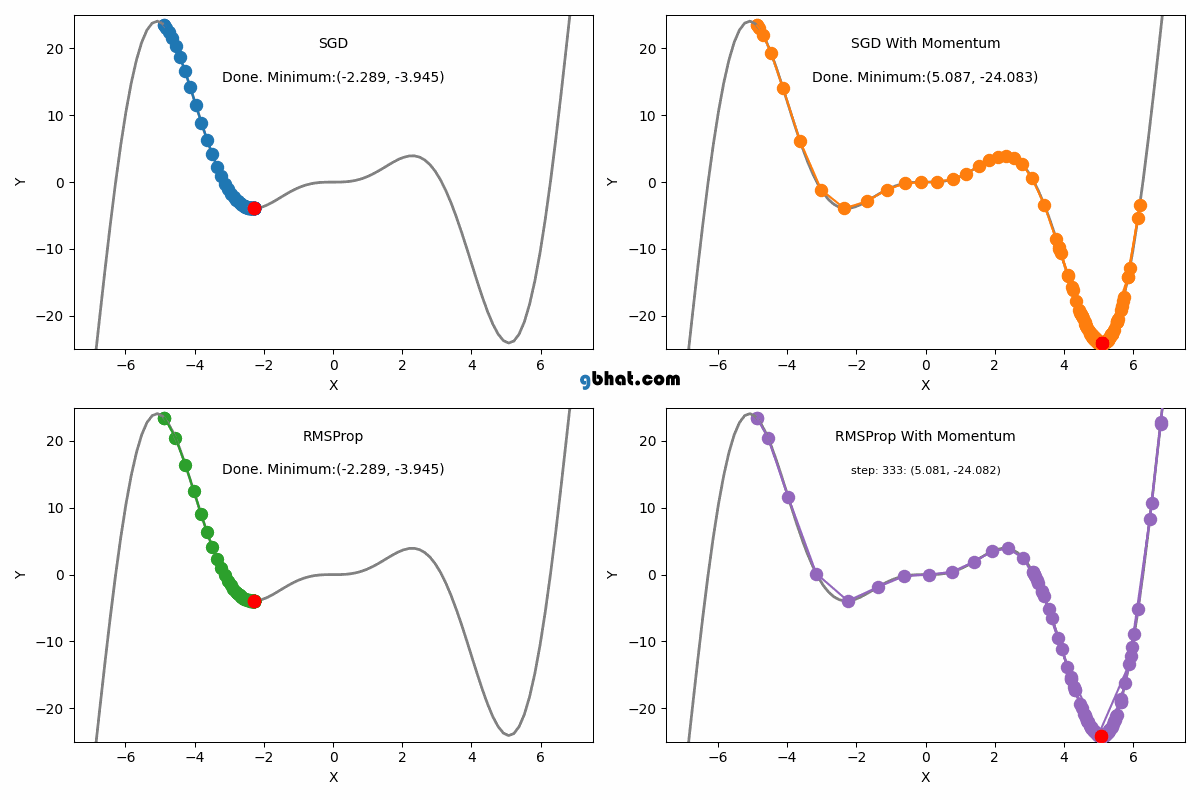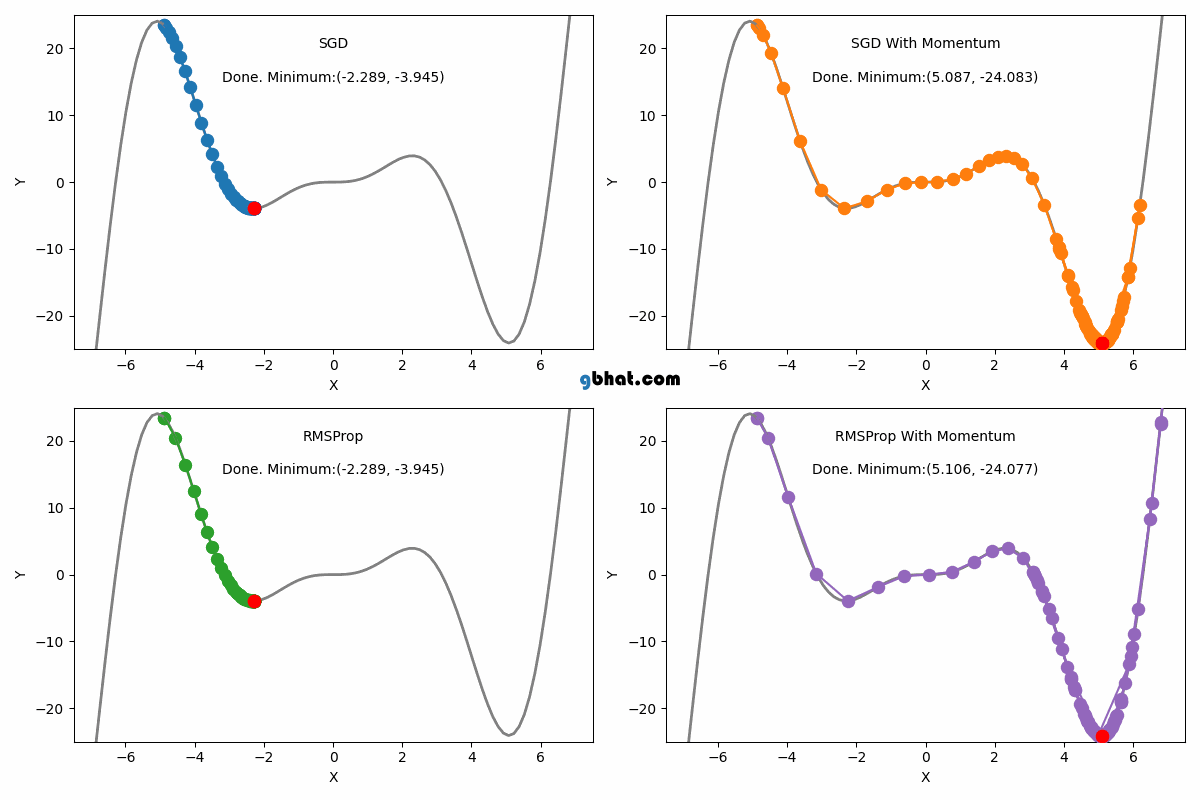
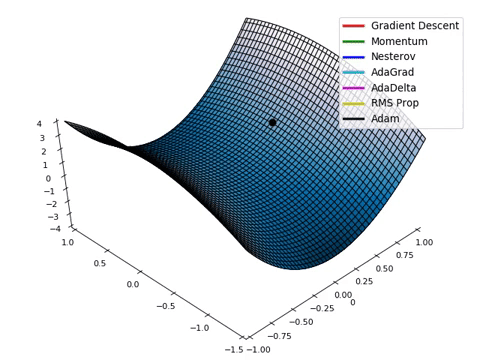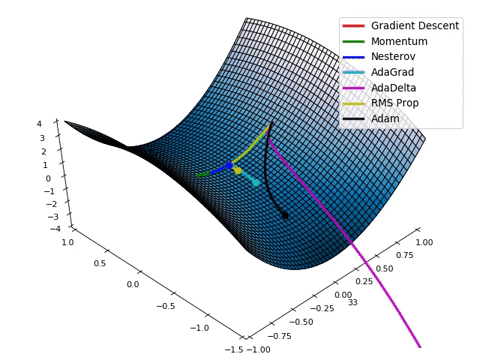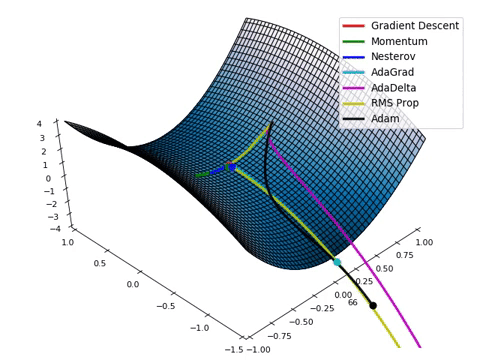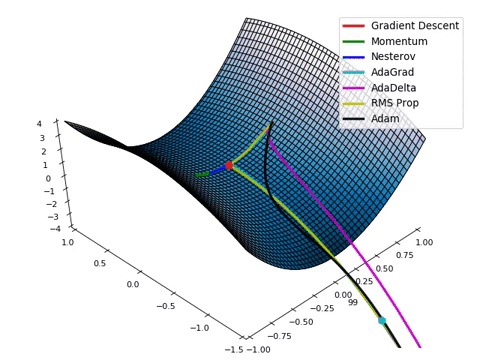
대표적인 Optimizer 종류

•
SGD(확률적 경사 하강법)
◦
각 데이터 샘플을 하나씩 학습시키는 방식
◦
빠르지만, 기울기가 불안정하고 최솟값 근처에서 진동할 수 있다.
◦
랜덤하게 추출한 일부 데이터를 사용해 더 빨리, 자주 업데이트를 하게 하는 것
◦
효과: 속도 개선
•
Momentum
◦
경사 하강법의 개선된 버전으로, 이전 기울기를 반영하여 관성을 추가한 방식
◦
기울기가 흔들리는 문제를 줄이고, 더 빠르게 수렴할 수 있다.
◦
기존 업데이트에 사용했던 경사의 일정 비율을 남겨서 현재의 경사와 더하여 업데이트함
◦
효과: 정확도 개선
•
Adagrad
◦
각 파라미터의 update 정도의 따라 학습률의 크기를 다르게 해줌
◦
자주 업데이트되는 가중치에 대해서는 학습률을 낮추고, 덜 업데이트되는 가중치에 대해서는 학습률을 높이는 방식
◦
학습률을 각 파라미터에 맞추어 조정하는 알고리즘
◦
효과: 보폭 크기 개선
•
RMSProp
◦
AdaGrad의 학습률 감소 문제를 해결하기 위해 지수 가중 평균을 사용해 기울기의 제곱값을 조정하여 학습률이 너무 빠르게 줄어들지 않도록 한다.
◦
이전 update 맥락을 보면서 학습률 조정하여 최신 기울기를 더 크게 반영
◦
효과: 보폭 크기 개선
•
Adam
◦
Momentum 과 RMSProp 장점을 결합한 알고리즘
◦
학습률을 적응적으로 조정하고, 이전 기울기의 1차 및 2차 모멘텀을 고려하여 가중치를 업데이트
◦
가장 많이 사용하는 Optimizer
◦
효과: 정확도와 보폭 크기 개선

정리

•
미니배치학습을 위한 데이터셋을 구성
•
딥러닝 모델인 인공신경망을 구현
•
우리가 풀고자하는 문제에 맞는 손실함수 사용
•
경사하강법에 문제를 보완하기 위해 적절한 옵티마이저를 선택
•
학습 과정
◦
데이터셋을 딥러닝 모델에 넣는다.
◦
예측 결과에 대한 손실을 구한다.
◦
역전파를 통해 모델 가중치의 기울기를 구한다.
◦
옵티마이저를 이용하여 모델 가중치를 업데이트한다.