Search

고유값과 고유벡터, 고유값 분해

대분류
인공지능/데이터
소분류
AI 수학
유형
선형 대수학
부유형
고유값
고유벡터
고유값 분해
주요 레퍼런스
https://bkshin.tistory.com/entry/%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D-19-%ED%96%89%EB%A0%AC
최종 편집 일시
2024/10/27 15:31
생성 일시
2024/07/19 01:22
13 more properties

고유값과 고유벡터

•
정방 행렬 A를 선형 변환으로 봤을 때, 선형 변환 A에 의한 변환 결과가 자기 자신의 상수 배가 되는 0이 아닌 벡터를 고유벡터(eigenvector)라고 하고, 이 상수배 값을 고유값(eigenvalue)이라 칭한다.
Av=λvAv = λv
정방 행렬 A에 대해서 Av =λvAv = λv를 만족하는 0이 아닌 열벡터 v = 고유 벡터, 상수 λ = 고유값
고유값, 고유 벡터는 정방 행렬에 대해서만 정의 정방 행렬 : 행(row)과 열(column)의 수가 같은 행렬을 의미 (n×m: n=m)
•
어떠한 선형 변환 A를 했을 때, 그 크기만 변하고 방향이 변하지 않는 벡터
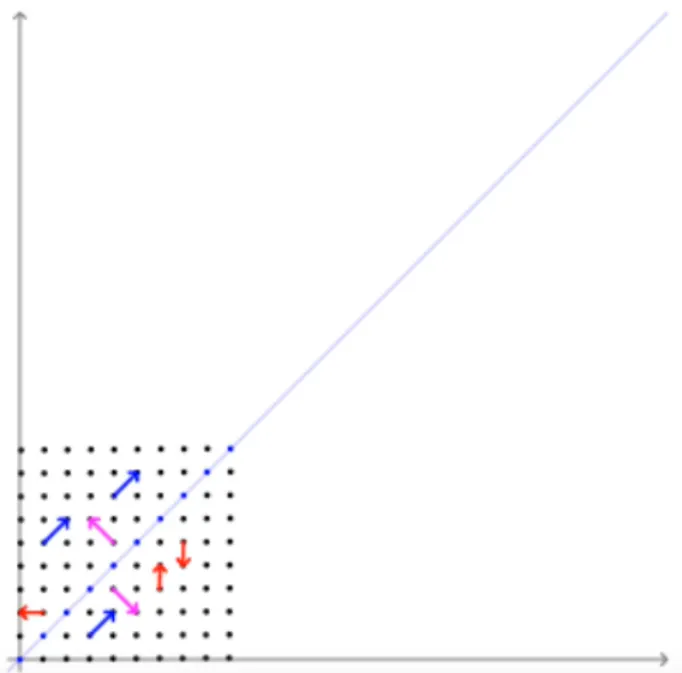
그림1 (출처: 공돌이의 수학정리노트 유튜브)
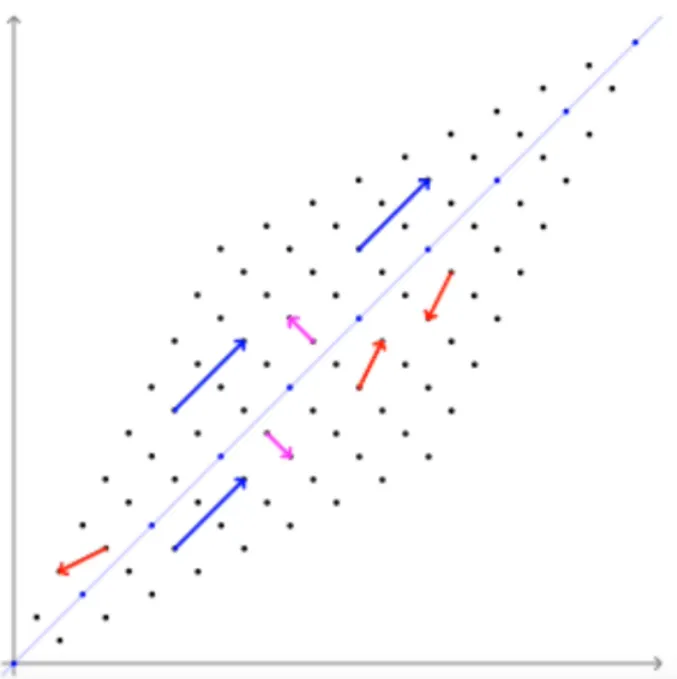
그림2 (출처: 공돌이의 수학정리노트 유튜브)
•
어떠한 선형 변환 A를 했을 때, 그 크기만 변하고 방향이 변하지 않는 벡터 ⇒ 고유값과 고유벡터가 존재
1.
파란색 벡터
•
파란색 벡터는 선형 변환 후 크기만 변하고 방향은 유지 ⇒ 고유벡터
•
고유값은 (그림 2의 파란색 벡터 크기 / 그림 1의 파란색 벡터 크기) == 즉, 증가한 벡터 크기 비율
2.
빨간색 벡터
•
빨간색 벡터는 선형 변환후 방향과 크기가 모두 변함 ⇒ 방향이 바꼈으므로 고유 벡터가 아니다.
3.
분홍색 벡터
•
분홍색 벡터는 선형 변환 후 크기도 방향도 유지 ⇒ 고유벡터
•
따라서 분홍색 벡터도 고유 벡터이며, 고유값은 벡터 크기가 동일하므로 1

고유값

•
행렬 𝐴의 고윳값은 다음 식을 만족하는 스칼라 값 𝜆
det⁡(𝐴−𝜆𝐼)=0det⁡(𝐴−𝜆𝐼)=0
◦
det는 행렬의 행렬식(determinant), 𝐼는 단위 행렬
◦
고유값은 해당 행렬이 어떤 선형 변환을 가지고 있는지, 그 변환 중에서 큰 변화가 일어나는 값으로 해석
◦
예를 들어, 주어진 행렬이 고윳값 𝜆를 갖는다면, 해당 행렬의 변환은 𝜆만큼 크기가 변하는 효과를 가지게 된다.

고유벡터 (Eigenvectors):

•
고유벡터는 해당 고윳값에 대응하는 벡터로, 다음 식을 만족
(𝐴−𝜆𝐼)𝑣=0(𝐴−𝜆𝐼)𝑣=0
◦
𝑣는 고유벡터이며, 𝜆는 고윳값
◦
고유벡터는 행렬이 가진 선형 변환에서 크기만 변하지 않고 방향만 변하는 특별한 벡터를 표시
◦
즉, 행렬이 적용될 때 고유벡터의 방향은 변하지 않고, 그 크기만 상수 배만큼 변할 뿐
◦
주로 주성분 분석, 특이값 분해 등 다양한 응용에서 사용

고유값 분해(eigen decomposition)

•
행렬 A의 고유값을 λiλ_i, 고유벡터를 vi,i=1,2,...,nv_i, i = 1, 2, ..., n이라 하였을 때
Av1=𝜆1v1Av2=𝜆2v2⋮Avn=𝜆nvnAv_1=𝜆_1v_1 \\ Av_2=𝜆_2v_2 \\ \vdots \\ Av_n=𝜆_nv_n
해당 식을 행렬로 나타내면
A[v1v2…vn]=[𝜆1v1𝜆2v2…𝜆nvn] =[v1v2…vn][𝜆10𝜆2⋱0𝜆n]A[v_1v_2\dots v_n]=[𝜆_1v_1𝜆_2v_2\dots 𝜆_nv_n] \\ \space \\ =[v_1v_2\dots v_n] \begin{bmatrix}𝜆_1 & & & 0 \\ & 𝜆_2 & & \\ & & \ddots & \\ 0 & & & 𝜆_n \end{bmatrix}
•
행렬 A를 고유 벡터와 고유값으로 분해
AP=PΛA=PΛP−1AP = PΛ \\ A = PΛP^{-1}
◦
P =행렬 A의 고유 벡터들을 열벡터로 하는 행렬
◦
Λ = 고유값을 대각원소로 가지는 대각 행렬

고유값 분해 수식

A=(−5401), I는 단위행렬,det는 행렬식 A= \begin{pmatrix} -5 & 4 \\ 0 & 1 \end{pmatrix},\space I는\space단위행렬,det는\space행렬식
det⁡(xI−A)=(x−(−5)−4−0x−(1))=x2−(−5+1)x+(−5−0)=x2+4x−5\begin{align*}\det(xI-A)&=\begin{pmatrix}x-(-5) & -4 \\-0 & x-(1)\end{pmatrix}\\ &=x^2-(-5+1)x+(-5-0)\\ &=x^2 + 4 x -5\end{align*}
x2+4x−5=0x=1  ,  −5x^2 + 4 x -5 = 0 \\ x= 1 \;,\; -5
이어서 x=−5x = -5일 때,
((−5)−(−5)−4−0(−5)−(1))(0−40−6)(x1x2)=(00)−4x2=0−6x2=0x2=0(x1x2)=(x10)=x1(10)\begin{align*} \begin{pmatrix} (-5)-(-5) & -4 \\ -0 & (-5)-(1) \end{pmatrix} \\ \begin{pmatrix} 0 & -4 \\ 0 & -6 \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} \\ -4 x_2 = 0 \\ -6 x_2 = 0 \\ x_2 = 0 \\ \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} = \begin{pmatrix} x_1 \\ 0 \end{pmatrix} = x_1 \begin{pmatrix} 1 \\ 0 \end{pmatrix} \end{align*}
x=1x = 1일 때,,
((1)−(−5)−4−0(1)−(1))(6−400)(x1x2)=(00)6x1+−4x2=06x1=4x2x1=4x26x1=23x2(x1x2)=(23x2x2)=x2(231)\begin{align*} \begin{pmatrix} (1)-(-5) & -4 \\ -0 & (1)-(1) \end{pmatrix} \\ \begin{pmatrix} 6 & -4 \\ 0 & 0 \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} \\ 6x_1 + -4x_2 = 0 \\ 6x_1 = 4x_2 \\ x_1 = {{4x_2} \over{6}} \\ x_1 = {{2} \over{3}}x_2 \\ \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} = \begin{pmatrix} {{2} \over{3}}x_2 \\ x_2 \end{pmatrix} = x_2 \begin{pmatrix} {{2} \over{3}} \\ 1 \end{pmatrix}&& \end{align*}
고유 벡터의 순서에서 고유벡터행렬P를 얻고 ,
(12301)\begin{pmatrix} 1 & {{2} \over{3}} \\ 0 & 1 \\ \end{pmatrix}
이어서 P−1AP=ADP^{-1}AP = A^{D}로 부터 대각화 행렬 ADA^D을 얻는다.
( 1 −23 0 1)( −54 01)( 1 23 0 1)=( −50 01)\begin{pmatrix} 1 &  -{{2} \over{3}} \\ 0 &  1 \\\end{pmatrix} \begin{pmatrix} -5 & 4 \\ 0 & 1\end{pmatrix} \begin{pmatrix} 1 &  {{2} \over{3}} \\ 0 &  1 \\\end{pmatrix}=\begin{pmatrix} -5 & 0 \\ 0 & 1\end{pmatrix}
P−1AP=ADPP−1AP=PADAP=PAD APP−1=PADP−1A=PADP−1P^{-1}AP = A^{D} \\ PP^{-1}AP = PA^{D} \\ AP = {P} { A^{D}} \\ \space \\ AP{P^{-1}} = {P} { A^{D}}{P^{-1}} \\ A = {P} { A^{D}}{P^{-1}}
행렬 A에 대한 고윳값 분해는 다음과 같다.
( −54 01)=( 1 23 0 1)( −50 01)( 1 −23 0 1)\begin{pmatrix} -5 & 4 \\ 0 & 1\end{pmatrix} = \begin{pmatrix} 1 &  {{2} \over{3}} \\ 0 &  1 \\\end{pmatrix} \begin{pmatrix} -5 & 0 \\ 0 & 1\end{pmatrix} \begin{pmatrix} 1 &  -{{2} \over{3}} \\ 0 &  1 \\\end{pmatrix}

특수한 경우

•
임의의 행렬A와 Λ가 대각행렬일 때
A=QΛQ−1A = QΛQ^{-1}
◦
QQ는 직교행렬
◦
Q−1Q^{-1}는 역행렬
◦
A는ADA는 A^{D}
•
임의의 행렬 A 가 대칭행렬일 때
A=QΛQTA = QΛQ^{T}
◦
QQ는 직교행렬
◦
Q−1Q^{-1}는 전치행렬
◦
A는ADA는 A^{D}