Search

확률과 통계

대분류
인공지능/데이터
소분류
통계 실험
유형
확률과 통계
부유형
순열 조합
확률 변수와 확률 분포
통계
모집단
자료
산포
상관
주요 레퍼런스
https://bb-dochi.tistory.com/47
https://ko.d2l.ai/chapter_crashcourse/probability.html
https://github.com/good593/course_ai/blob/main/math/%ED%86%B5%EA%B3%84%20%26%20%ED%99%95%EB%A5%A01.ipynb
최종 편집 일시
2024/10/29 08:50
생성 일시
2024/07/31 03:14
13 more properties

순열, 조합

순열

•
서로 다른 N개에서 중복을 허락하지 않고 r개를 일렬로 나열하는 수
nPr=n!(n−r)!_nP_r=\frac{n!}{(n-r)!}

중복 순열

•
서로 다른 N개에서 중복을 허락하고 r개를 일렬로 나열하는 수
nΠr=nr_n\Pi_r = n^r

조합(Combination)

•
서로 다른 n개로부터 중복 없이 r개를 골라내는 경우의 수
nCr=n!(n−r)!r!=nPrr!_nC_r = \frac{n!}{(n-r)!r!} = \frac{_nP_r}{r!}

중복 조합

•
서로 다른 N개에서 순서를 생각하지 않고 중복을 허락하여 r개를 선택
nHr=n+r−1Cr=(n−r−1)!(n−2r−1)!r!_nH_r = _{n+r-1}C_r = \frac{(n-r-1)!}{(n-2r-1)!r!}

순열과 조합의 차이

1. 대표 뽑기
•
순열) 4명 중 반장, 부반장을 뽑을 때 경우의 수
◦
서로 다른 4명이고 반장, 부반장을 뽑는다 (순서o)
4P2_4P_2
•
조합) 4명 중 대표를 2명 뽑을 때 경우의 수
◦
서로 다른 4명이고 대표를 2명 뽑는다 (순서x)
4C2_4C_2
2. 후보 2명, 유권자 6명일 때 - 무기명 투표, 기명 투표
•
중복순열) 기명 투표 (내가 A, 친구가 B뽑은 것과 / 친구가 A, 내가 B 뽑은 것은 다른 것)
2Π6=26_2\Pi_6 = 2^6
•
중복조합) 무기명 투표
2H6=7C6=7C1_2H_6 = _7C_6=_7C_1

확률

확률(Probability)

•
어떤 사건이 우연히 발생할 가능성 표현
P=어떤 일이 일어날 경우의 수모든 경우의 수P= \frac{어떤\space일이\space일어날\space경우의\space수}{모든\space경우의\space수}

통계

•
집단에 대해 집단의 현상을 체계적인 숫자로 표현한 것

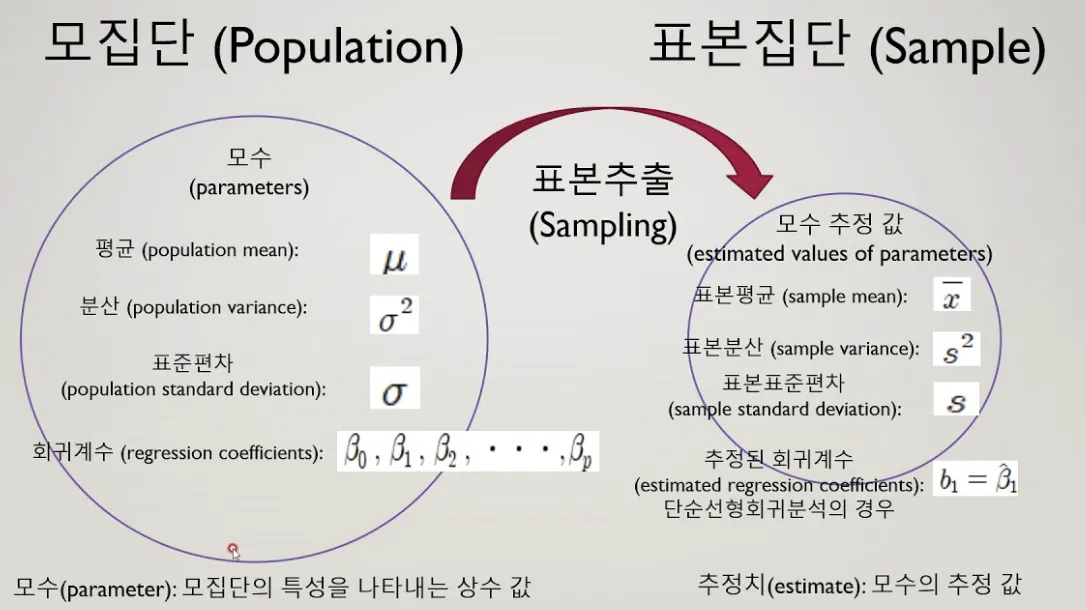
모집단/모수/표본/통계량

모집단(Poplulation)

•
통계학에서 관심/조사의 대상이 되는 개체의 전체 집합

모수(Parameter)

•
모집단에 대한 수치적 요약
◦
고등학생의 1일 평균 온라인게임 플레이 시간
◦
강아지보다 고양이를 좋아하는 성인의 비율

표본(Sample)

•
모집단을 적절히 대표하는 모집단의 일부

통계량(Statistic)

•
표본에 대한 수치적 요약
◦
고등학생 1000명의 1일 평균 온라인게임 플레이 시간
◦
강아지보다 고양이를 좋아하는 성인의 비율(1000명)
Sample statistic(표본 통계량)을 통해서 Population parameter(모집단 모수)를 예측하고 이해하는 과정이 통계의 목적이라고 생각

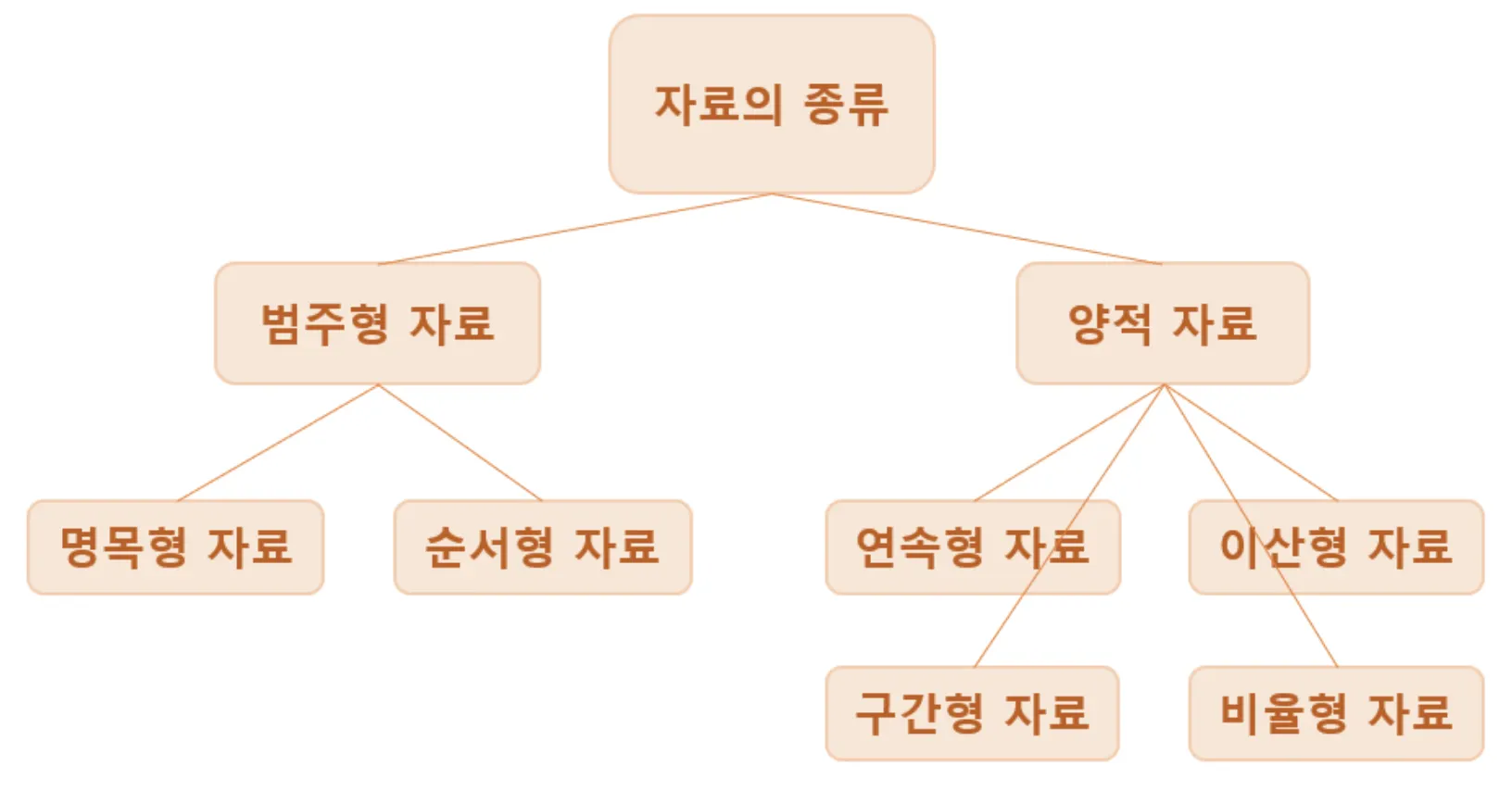
자료의 종류

범주형 자료

•
속성의 범주화, 상대적 서열도 표현
◦
명복형 자료: 단순히 속성을 분류하기 위함(혈액형)
◦
순서형 자료: 상대적인 크기 비교(만족도, 최종학력, 학점)

양적 자료

•
자료자체가 숫자로 표현됨
◦
이산형 자료: 셀 수 있음 (빈도 수, 불량품의 수, 주사위 확률)
◦
연속형 자료: 셀 수 없음 (길이, 시간)

통계량

최빈값(mode)

•
발생빈도가 가장 높은 값
•
극단값에 영향을 받지 않음
•
주로 범주형 자료에 대한 대표값
•
2개 이상 존재 가능

중앙값(median)

•
크기 순으로 정렬된 자료에서 가운데에 위치하는 값
•
관측값 변화에 민감하지 않음
•
극단값에 영향을 받지 않음

산술평균(Arithmetic Mean)

•
모든 자료의 값을 더하여 자료의 수로 나누어 준 값
•
모든 값을 반영하므로 극단값에 영향을 받음
xˉ=∑xin=x1+x2+...+xnn\bar{x} = { \sum{x_i} \over n } = { x_1 + x_2 + ... + x_n \over n }

가중평균(Weighted Mean)

•
자료의 중요성이 각기 다를 경우
•
중요도에 따라 가중치를 부여한 평균
Xˉ=∑wiXiˉ∑wi=w1X1ˉ+w2X2ˉ+...+wiXiˉw1+w2+...+wi\bar{X} = { \sum{w_i\bar{X_i}} \over \sum{w_i} } = { w_1\bar{X_1} + w_2\bar{X_2} + ... + w_i\bar{X_i} \over w_1 + w_2 + ... + w_i}

기하평균

•
자료가 성장률, 증가율 등 앞 시점에 대한 비율로 나타난 경우 유용한 통계량
•
음수가 아닌 자료값 only
•
연간 물가 상승률
◦
Ex) 일일 주가 상승률: 1% 3% 5% 10% : 1.0374....
기하평균(G)=∏nxin(xi=상승률)기하평균(G) = \sqrt[n]{ \prod^n x_i } \\ (x_i=상승률)

산포: 데이터의 퍼진 정도

편차(Deviation)

•
관측값에서 평균 또는 중앙값을 뺀 것
•
어떤 데이터셋(자료)에서 각각의 개별 값에서 평균을 뺀 값
xi−xˉx_i-\bar{x}

분산(Variance)

•
편차 제곱의 합을 자료의 수로 나눈 값
•
xˉ\bar{x}: 산술 평균
•
(xi−xˉ)2(x_i-\bar{x})^2: 편차 제곱
s2=∑n(xi−xˉ)2(n−1)s^2 = \sum^n{(x_i-\bar{x})^2 \over (n -1)}

표준편차(Standard Deviation)

•
분산을 제곱근한 값
s=s2=∑n(xi−xˉ)2(n−1)s = \sqrt{ s^2 } = \sqrt{ \sum^n{ (x_i - \bar{x})^2 \over (n-1) } }

형태: 데이터의 형태

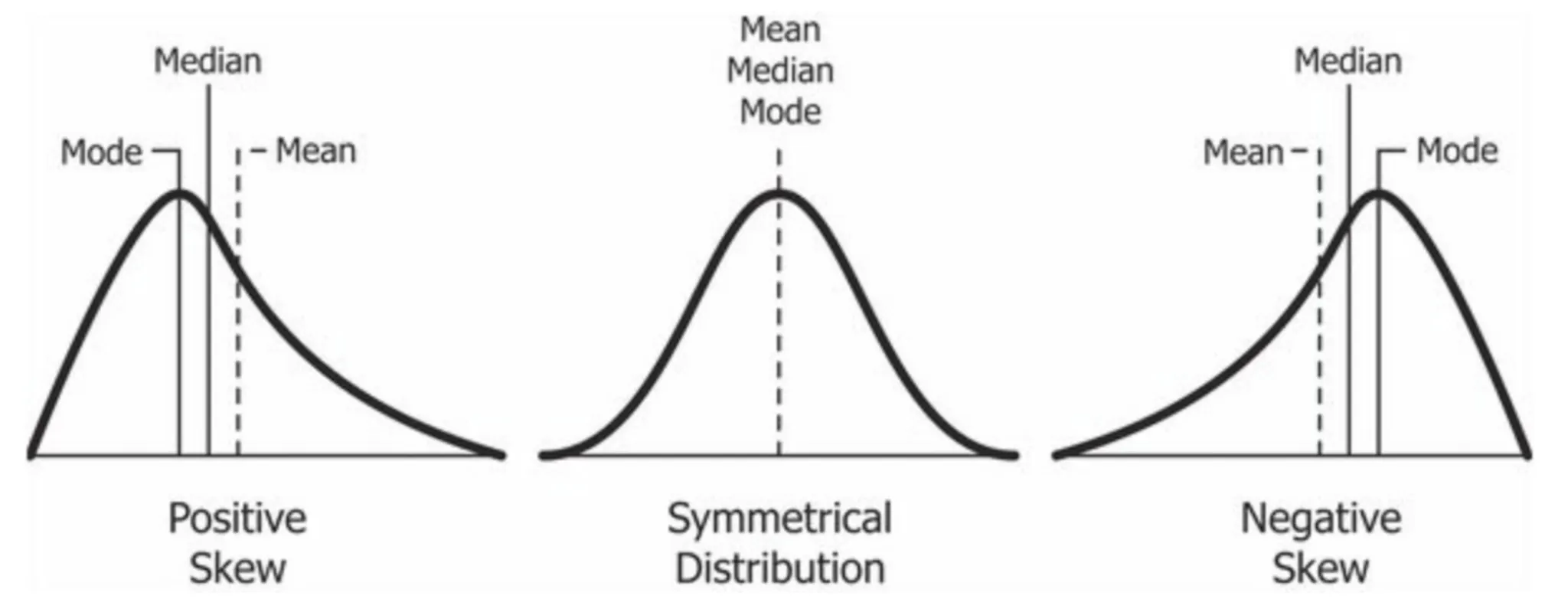
왜도(Skewness)

•
분포의 비대칭도
•
Mode(최빈값), Median(중앙값), Mean(산술평균)
<Positive Skew인 경우>
•
Mean > Median > Mode
<Symmetrical Distribution인 경우>
•
Mean = Median = Mode
<Negative Skew인 경우>
•
Mode > Median > Mean

첨도(Kurtosis)

•
뽀족한 정도
•
표준정규분포의 첨도는 3이 된다.
K=E[(X−μσ)4]−3=μ4σ4−3K = E\big[\big(\frac{X- \mu}{ \sigma}\big)^4\big]-3=\frac{\mu_4}{\sigma^4}-3
1.
K>0K > 0
•
표준정규분포보다 더 뾰족함
2.
K<0K < 0
•
표준정규분포보다 덜 뾰족함
3.
K=0K = 0
•
표준정규분포 정도의 뾰족함

선형적 관계

•
두 변수 간의 관계가 직선으로 표현될 수 있는 관계
•
두 변수 X와 Y 사이의 관계가 선형적이라는 것은, 그 관계를 다음과 같은 일차 함수로 표현할 수 있다는 것을 의미
Y=aX+bY = aX + b
◦
Y: 종속 변수(또는 반응 변수)
◦
X: 독립 변수(또는 설명 변수)
◦
a: 기울기(slope), X가 1 단위 증가할 때 Y가 얼마나 변하는지를 표시
◦
b: 절편(intercept), X가 0일 때 Y의 값

선형적 관계의 특징

•
직선 형태: 두 변수 간의 관계가 직선으로 나타납니다.
•
일정한 변화율: X가 일정하게 변화할 때 Y도 일정하게 변화
⇒ 즉, X가 1 단위 증가할 때마다 Y는 항상 a만큼 증가하거나 감소
•
양의 선형 관계: a>0일 때, X가 증가하면 Y도 증가
•
음의 선형 관계: a<0일 때, X가 증가하면 Y는 감소

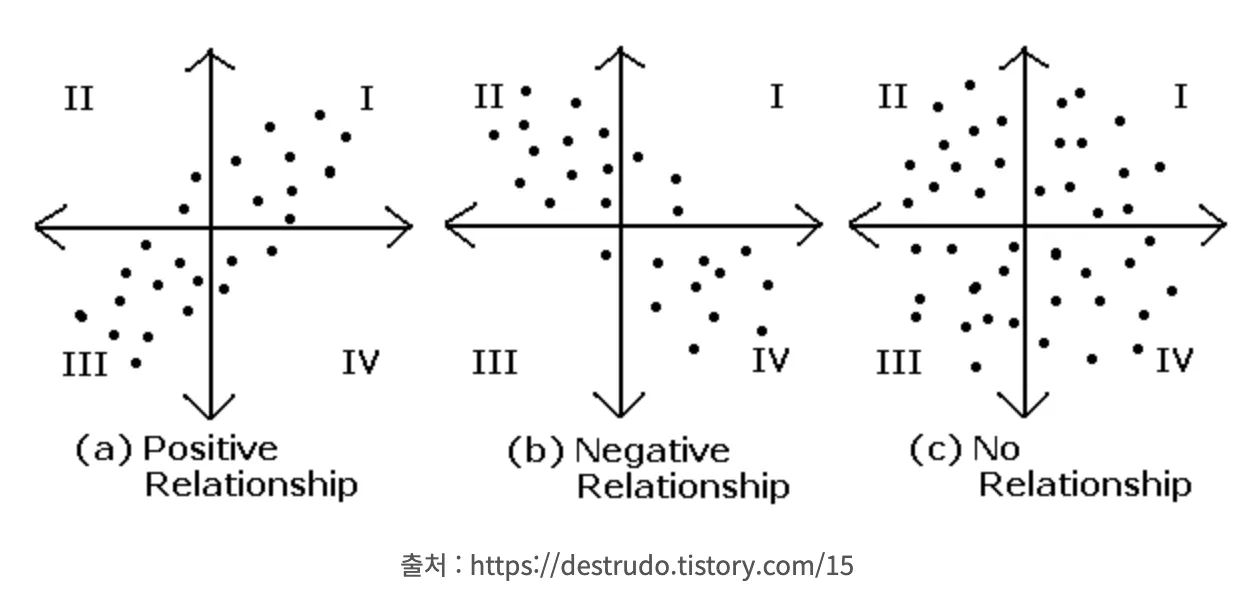
상관: 데이터간의 상관관계 표현

•
상관(Correlation)이란?
◦
확률변수 X,Y의 변화가 서로 관계가 일을 때 상관관계가 있다고 함
◦
두 변수 간의 관계를 수치로 표현
◦
한 변수의 변화가 다른 변수의 변화와 어떻게 관련이 있는지를 나타냄
◦
선형적 관련성을 파악함

공분산(Covariance)

•
공분산 (Covariance, Cov)는 2개의 확률변수의 상관 정도를 나타내는 값
•
(xi−x‾)(x_i−\overline{x}): X 편차
•
(yi−y‾)(y_i−\overline{y}): Y 편차
sxy=∑(xi−xˉ)(yi−yˉ)n−1s_{xy} = { \sum{(x_i - \bar{x})(y_i - \bar{y})} \over n - 1 }
◦
XiX_i와 YiY_i : 각각 X와 Y의 데이터 포인트
◦
x‾\overline{x}와 y‾ \overline{y} : 각각 X와 Y의 평균값
◦
n : 데이터 포인트의 수
•
해석
◦
양의 공분산
▪
X와 Y가 함께 증가하는 경향이 있음을 나타낸다.
▪
즉, X가 증가할 때 Y도 증가하는 경우가 많다.
◦
음의 공분산
▪
X와 Y가 반대 방향으로 변동하는 경향이 있음을 나타낸다.
▪
즉, X가 증가할 때 Y는 감소하는 경우가 많다.
◦
공분산이 0
▪
두 변수 간에 선형적 관계가 거의 없음을 의미
▪
즉, X와 Y는 서로 독립적으로 변화할 가능성이 높다

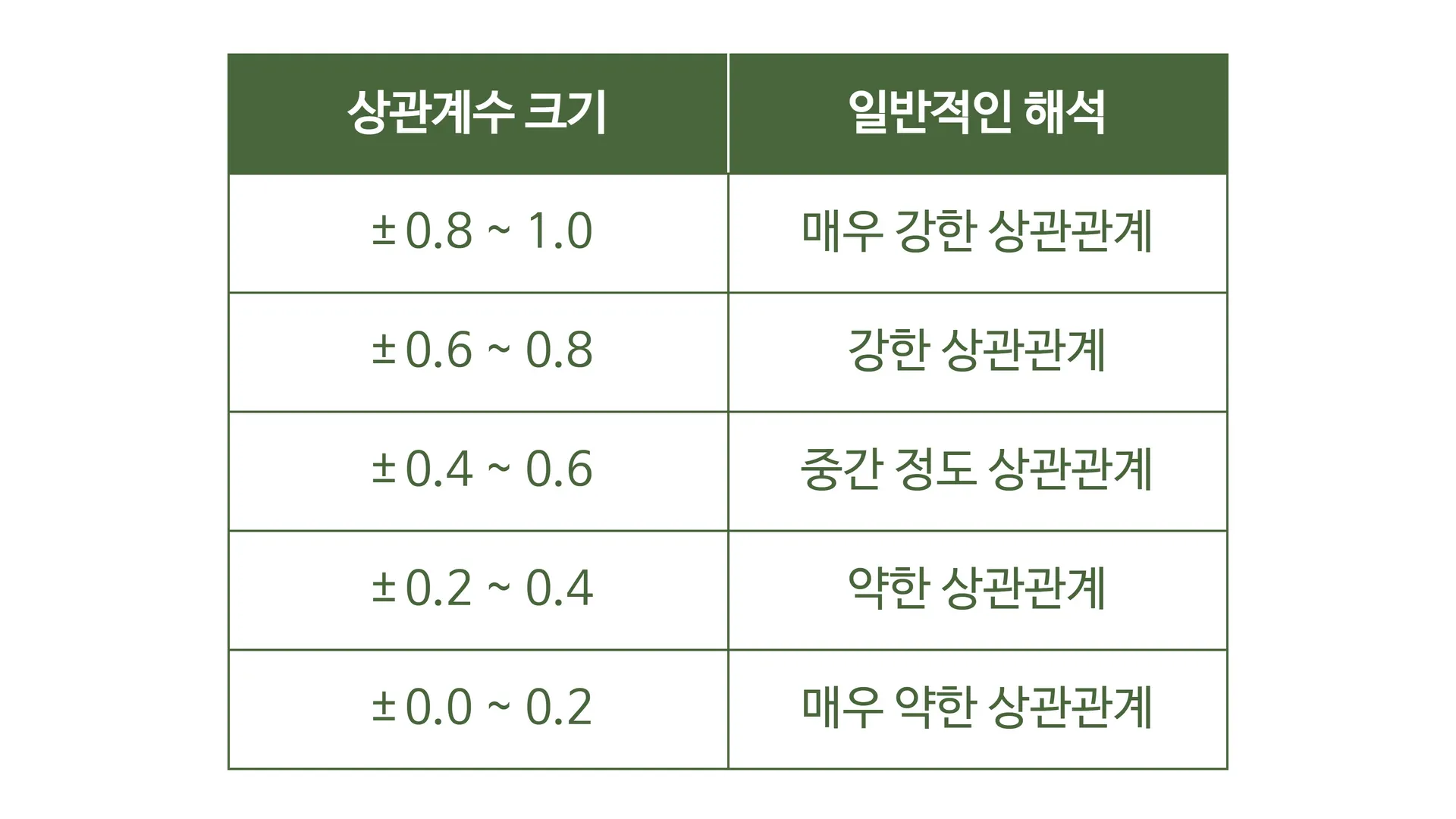
상관계수

•
상관 계수의 해석
•
상관의 정도를 나타내는 값 == 두 데이터 사이의 선형 관계를 반영하는 수치
•
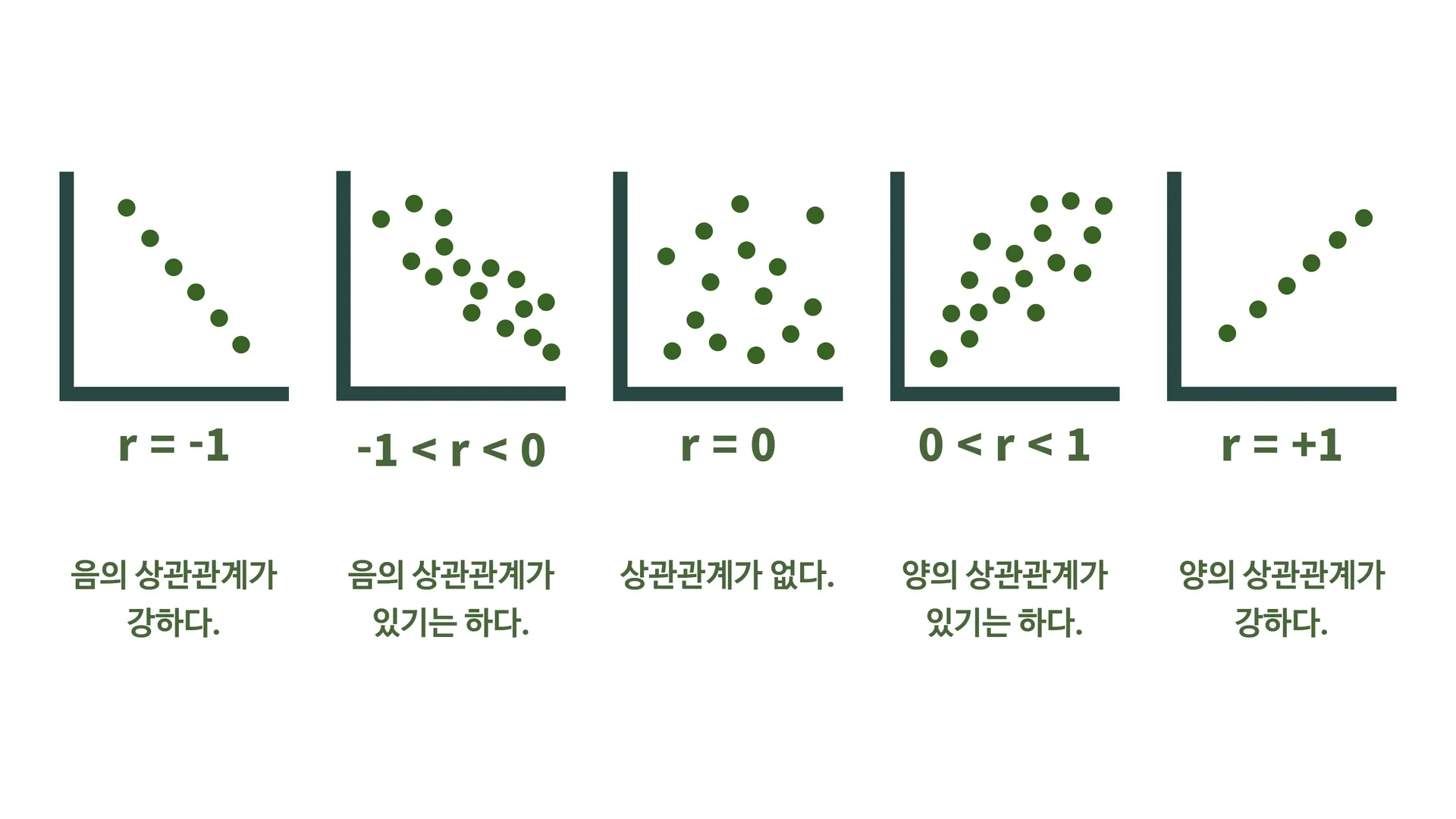
표기: 보통 r로 표기하며, 값은 1에서 1 사이입니다.
◦
r = 1: 완벽한 양의 선형 상관관계 (두 변수는 같은 방향으로 변화함)
◦
r = -1: 완벽한 음의 선형 상관관계 (두 변수는 반대 방향으로 변화함)
◦
r = 0: 상관관계가 없음 (두 변수 간에 선형적 관계가 없음)
•
가장 흔히 사용되는 상관 계수 : 피어슨 상관계수
•
피어슨 상관계수(Pearson’s Correlation Coefficient)
◦
확률 변수의 절대적 크기에 영향을 받지 않도록 공분산을 단위화 시킨 것
rxy=∑(xi−xˉ)(yi−yˉ)∑(xi−xˉ)2∑(yi−yˉ)2−1<=r<=1r_{xy} = { \sum{(x_i - \bar{x})(y_i - \bar{y})} \over \sqrt{ \sum{(x_i - \bar{x})^2 \sum{(y_i - \bar{y})^2}} } } \qquad -1 <= r <= 1

공분산의 단점

•
공분산은 단순한 상관관계의 방향만을 알려준다.
•
상관관계의 정도는 알 수 없다.(확률 변수의 단위크기가 크면 무조건 공분산의 크기가 크게 나오는 문제가 있다.)

상관계수의 성질

•
공분산을 두 변수의 표준편차의 곱으로 나눈 값
•
두 양적 변수 간의 선형적 연관성의 강도 측정
•
단위가 없음
•
상관관계가
◦
0<ρ<=1이면 양의 상관
◦
−1<=ρ<0이면 음의 상관
◦
ρ=0이면 무상관