분류 모델
분류의 선형 모델
분류형 선형 모델에서는 경정 경계가 입력의 선형 함수입니다. 다른 말로하면 이진 선형 분류기는 선, 평면, 초평면을 사용해서 두 개의 클래스를 구분하는 분류기입니다.
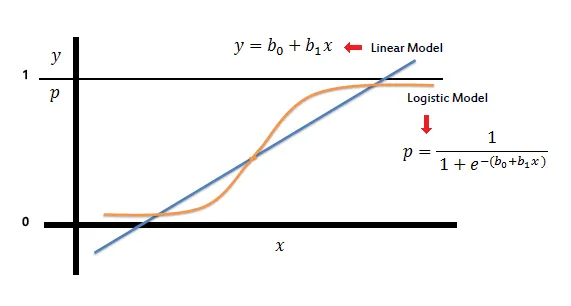
로지스틱 회귀(Logsitic Regression)
•
예측 결정으로 시그모이드 함수 사용
•
시그모이드함수
e는 자연상수
◦
입력값이 양수 무한대로 입력이 들어가도 1에 가깝게 출력
◦
입력값이 음수 무한대로 입력이 들어가도 0에 가깝게 출력
•
예제 : 유방암
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
X_tr, X_te, y_tr, y_te = train_test_split(
cancer.data, cancer.target, stratify=cancer.target, random_state=42
)
logreg = LogisticRegression().fit(X_tr, y_tr)
> print(f'훈련용 평가지표: {logreg.score(X_tr, y_tr)} / 테스트용 평가지표: {logreg.score(X_te, y_te)}')
훈련용 평가지표: 0.9460093896713615 / 테스트용 평가지표: 0.958041958041958
logreg100 = LogisticRegression(C=100).fit(X_tr, y_tr)
> print(f'훈련용 평가지표: {logreg100.score(X_tr, y_tr)} / 테스트용 평가지표: {logreg100.score(X_te, y_te)}')
훈련용 평가지표: 0.9436619718309859 / 테스트용 평가지표: 0.958041958041958
logreg001 = LogisticRegression(C=0.01).fit(X_tr, y_tr)
> print(f'훈련용 평가지표: {logreg001.score(X_tr, y_tr)} / 테스트용 평가지표: {logreg001.score(X_te, y_te)}')
훈련용 평가지표: 0.9342723004694836 / 테스트용 평가지표: 0.9300699300699301
Python
복사
◦
훈련용 평가지표와 테스트용 평가지표가 비슷하게 나왔다. 이는 과소적합. 즉, 훈련이 덜되었다고 해석할 수 있다.
◦
하이퍼파리미터 C는 정규화(L2 규제)를 조절하는 값 : 해당 값은 꼭 양의 실수값이어야 한다.
◦
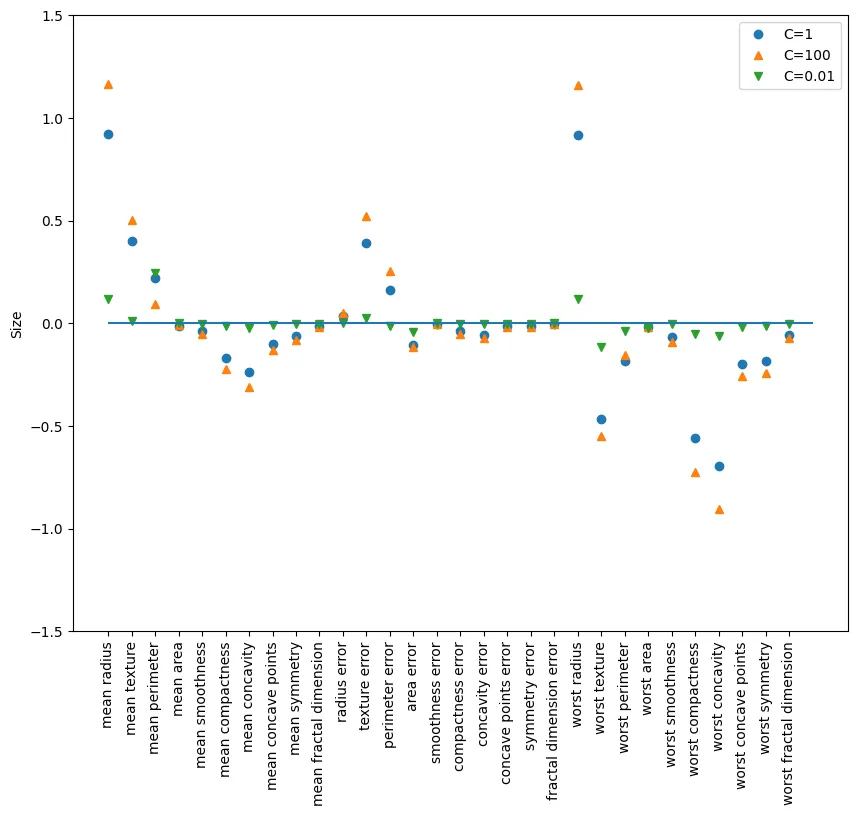
하이퍼파리미터 C이 낮을 수록 계수를 0으로 근사하므로 정규화가 강화된다고 해석할 수 있다.
plt.figure(figsize=(10,8))
plt.plot(logreg.coef_.T, 'o', label='C=1')
plt.plot(logreg100.coef_.T, '^', label='C=100')
plt.plot(logreg001.coef_.T, 'v', label='C=0.01')
plt.xticks(range(cancer.data.shape[1]), cancer.feature_names, rotation=90)
plt.hlines(0,0, cancer.data.shape[1])
plt.ylim(-1.5,1.5)
# plt.xlabel("특성")
plt.ylabel("Size") # 계수 크기
plt.legend()
Python
복사
선형 서포트벡터 머신(Linear SVM)
•
클래스를 구분하는 분류 문제에서 각 클래스를 잘 구분하는 선을 그어주는 방식
•
두 클래스의 가운데 선을 그어주게될 때, 가장 가까이 있는 점들을 Support Vector라고 하며, 찾은 직선과 서포트벡터 사이의 거리를 최대 마진(margin)이라고 한다.
•
결구 마진을 최대로 하는 서포트벡터와 직선을 찾는 것이 목표이다.
•
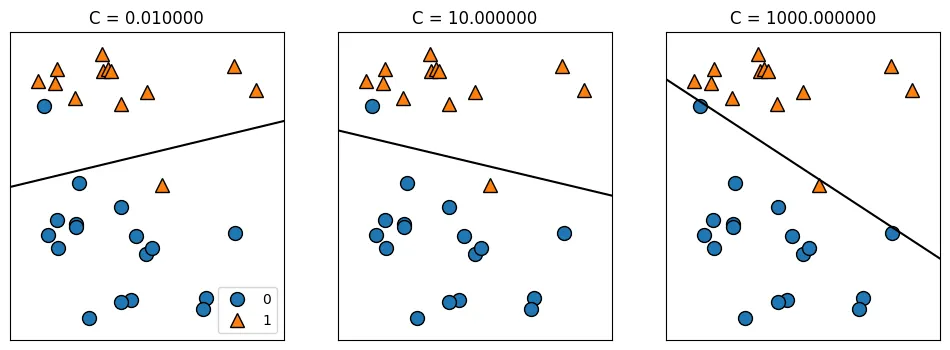
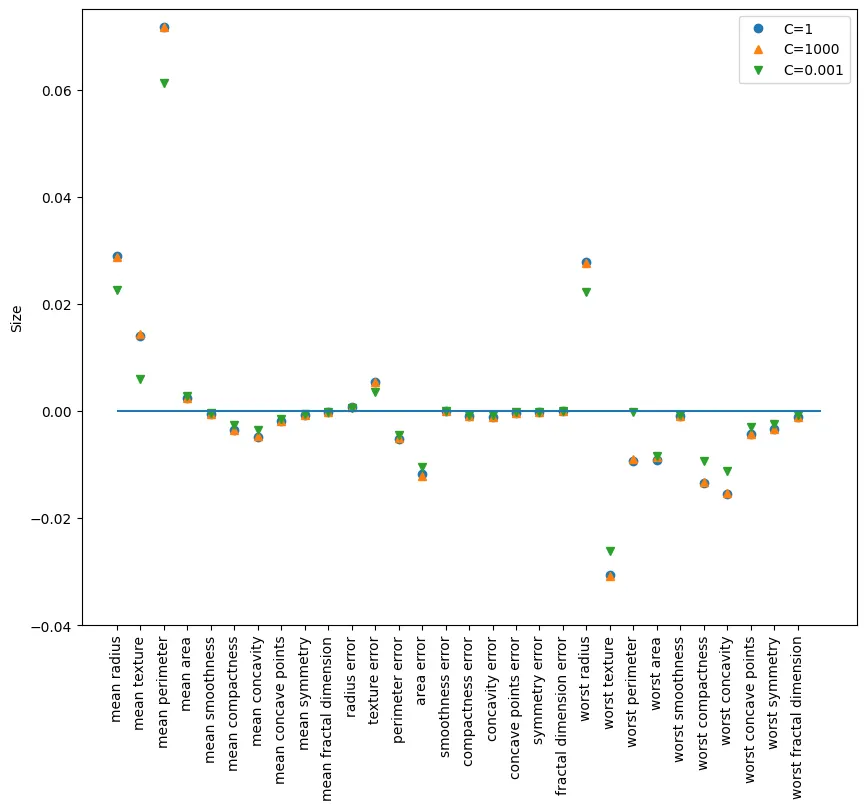
선형 서포트벡터 머신모델 역시, 하이퍼파리미터 C이 낮을 수록 계수를 0으로 근사하므로 정규화가 강화된다고 해석할 수 있다.
mglearn.plots.plot_linear_svc_regularization()
YAML
복사
lsvc100 = LinearSVC(C=1000).fit(X_tr, y_tr)
> print(f'훈련용 평가지표: {lsvc100.score(X_tr, y_tr)} / 테스트용 평가지표: {lsvc100.score(X_te, y_te)}')
훈련용 평가지표: 0.931924882629108 / 테스트용 평가지표: 0.9370629370629371
lsvc001 = LinearSVC(C=0.001).fit(X_tr, y_tr)
> print(f'훈련용 평가지표: {lsvc001.score(X_tr, y_tr)} / 테스트용 평가지표: {lsvc001.score(X_te, y_te)}')
훈련용 평가지표: 0.92018779342723 / 테스트용 평가지표: 0.9300699300699301
Python
복사
plt.figure(figsize=(10,8))
plt.plot(lsvc.coef_.T, 'o', label='C=1')
plt.plot(lsvc100.coef_.T, '^', label='C=1000')
plt.plot(lsvc001.coef_.T, 'v', label='C=0.001')
plt.xticks(range(cancer.data.shape[1]), cancer.feature_names, rotation=90)
plt.hlines(0,0, cancer.data.shape[1])
plt.ylim(-0.04,0.075)
# plt.xlabel("특성")
plt.ylabel("Size") # 계수 크기
plt.legend()
Python
복사
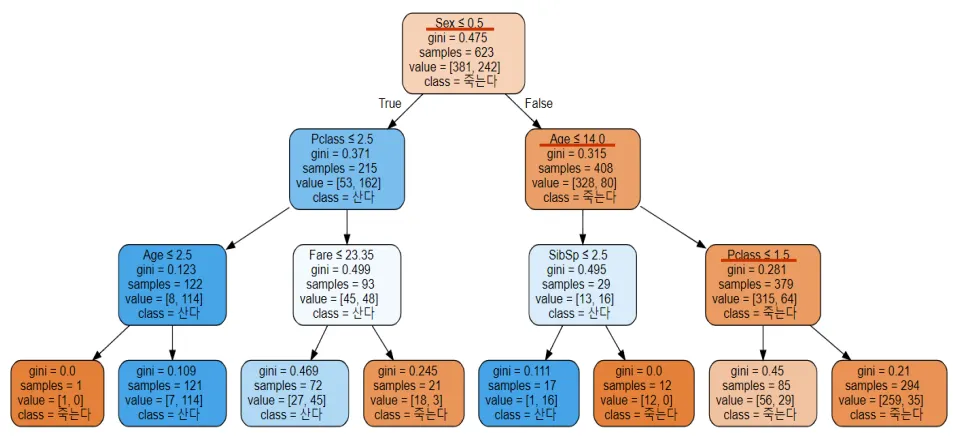
의사결정나무(Decision Tree)
•
회귀,분류 둘다 사용 가능한 알고리즘
•
여러가지 규칙을 순차적으로 적용하면서 트리기반의 규칙을 만들어 예측하는 알고리즘
•
데이터를 분할 하는데 순수도가 높은 방향으로 규칙을 정한다.
•
순수도
◦
각 노드의 규칙에 의해 동일한 클래스가 포함되는 정도를 의미
◦
부모노드의 순수도에 비해 자식노드들에 순수도가 증가하도록 트리를 형성
•
순수도 척도
◦
entropy: 엔트로피는 데이터의 혼자도를 의미한다. 엔트로피값이 0이 될때까지 계층이 만들어진다.
◦
gini: gini(불평등지수) 값이 0이면 평등하다는 것을(분류가 잘됐다). 뜻한다. 이 값 역시 0이 될때까지 계층이 만들어진다.
◦
gini, entropy값이 0에 가까울 수록 순수도가 높다는 뜻이다.
•
root node: 최상단에 위치한 노드(시작점)
•
leaf node: 더 이상의 규칙을 정할 수 없는 노드(결정된 클래스 값)
•
max nodes: gini/entropy값이 0이 되지 않더라도, max nodes 값 이상으로 노드를 만들지 않음
•
min samples split: 해당 노드가 가지고 있는 최소한의 샘플의 개수를 나타낸다.
•
min sample leaf: 또 다른 노드를 만들 수 있는 최소한의 샘플 수 조건을 뜻한다.
from sklearn.tree import DecisionTreeClassifier
cancer = load_breast_cancer()
X_tr, X_te, y_tr, y_te = train_test_split(
cancer.data, cancer.target, stratify=cancer.target, random_state=42
)
tree = DecisionTreeClassifier(random_state=0).fit(X_tr, y_tr)
> print(f'훈련용 평가지표: {tree.score(X_tr, y_tr)} / 테스트용 평가지표: {tree.score(X_te, y_te)}')
훈련용 평가지표: 1.0 / 테스트용 평가지표: 0.9370629370629371
Python
복사
hp = {
"random_state":42,
"max_depth":4 ,# 최대 깊이
"min_samples_split":2, # 노드를 분할하는데 필요한 최소한의 샘플수
"criterion" : "entropy", # 순수도 척도
"max_leaf_nodes" : 10, # 최대리프노드수, 과적합 방지
"min_samples_leaf" : 20, # 리프노드에 있어야할 최소 샘플수
}
tree = DecisionTreeClassifier(**hp).fit(X_tr, y_tr)
print(f'훈련용 평가지표: {tree.score(X_tr, y_tr)} / 테스트용 평가지표: {tree.score(X_te, y_te)}')
Python
복사
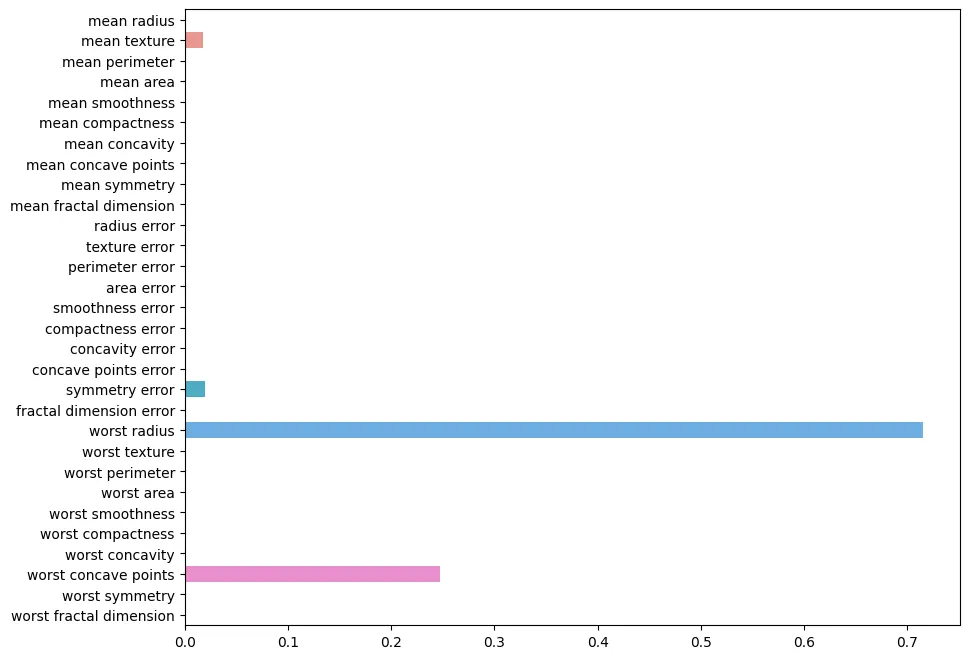
plt.figure(figsize=(10,8))
sns.barplot(x=tree.feature_importances_,y=cancer.feature_names)
plt.show()
Python
복사
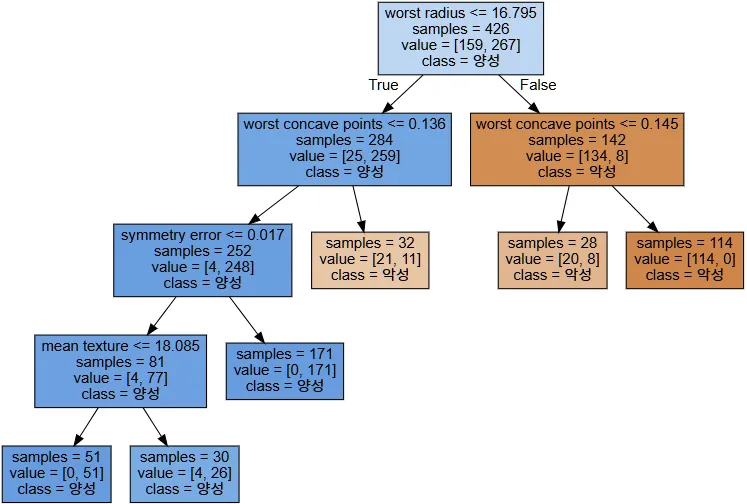
from sklearn.tree import export_graphviz
export_graphviz(
tree, out_file="tree.dot", class_names=["악성", "양성"],
feature_names=cancer.feature_names, impurity=False, filled=True)
import graphviz
with open("tree.dot") as f:
dot_graph = f.read()
display(graphviz.Source(dot_graph))
Python
복사
k-최근접 이웃(K-NN)
•
최근접 이웃 알고리즘
•
새로운 샘플이 K개의 가까운 이웃을 이용해서 예측
•
제일 가까운 데이터 포인트를 찾아서 결정하는 방식
•
회귀, 분류 둘다 사용한 알고리즘
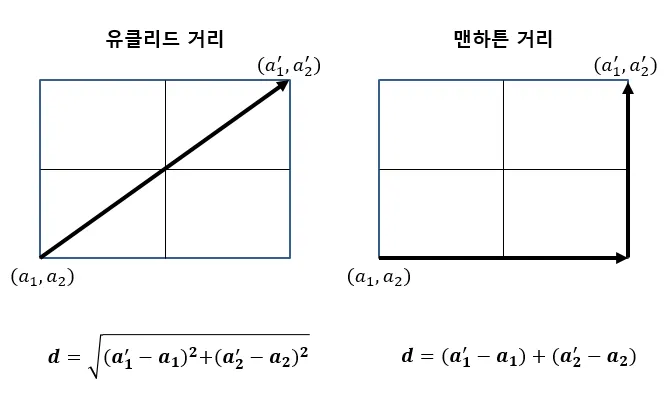
데이터 포인트간의 거리를 측정하는 방법
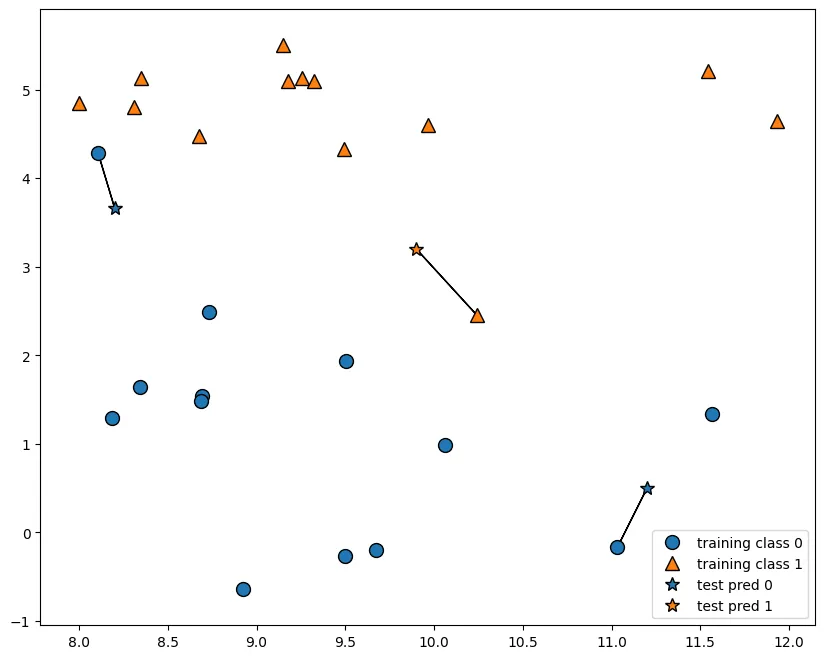
plt.figure(figsize=(10,8))
mglearn.plots.plot_knn_classification(n_neighbors=1)
Python
복사
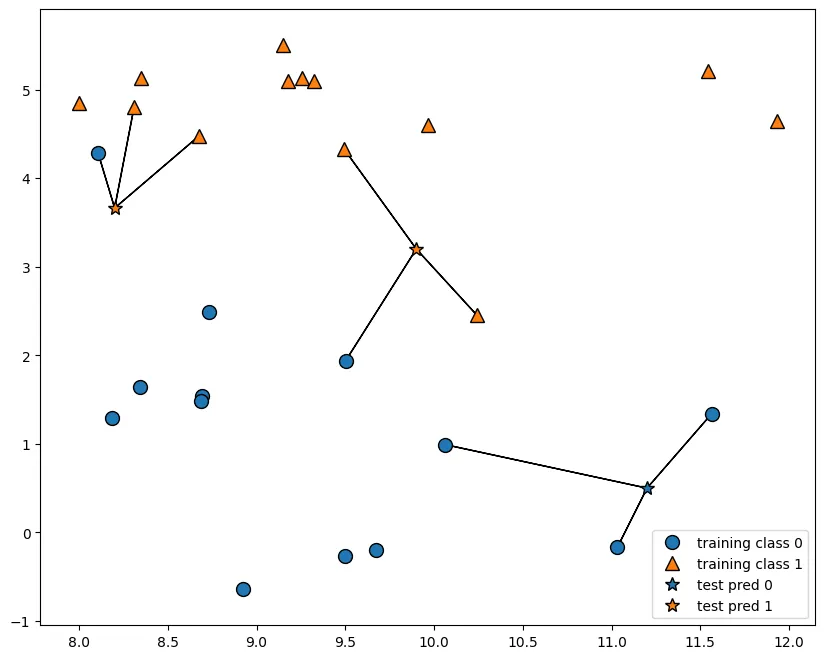
plt.figure(figsize=(10,8))
mglearn.plots.plot_knn_classification(n_neighbors=3)
Python
복사