라이브러리 로드
데이터 분석용 라이브러리
# 데이터 분석에 사용할 라이브러리
import pandas as pd
import numpy as np
Python
복사
import logging
logging.getLogger('matplotlib.font_manager').setLevel(logging.ERROR)
Python
복사
데이터 시각화용 라이브러리
# 데이터 시각화에 사용할 라이브러리
import matplotlib.pyplot as plt
import matplotlib as mpl
import seaborn as sns
# 브라우저에서 바로 그려지도록
%matplotlib inline
# 그래프에 retina display 적용
%config InlineBackend.figure_format = 'retina'
# Colab 의 한글 폰트 설정
plt.rc('font', family='NanumBarunGothic')
# 유니코드에서 음수 부호설정
mpl.rc('axes', unicode_minus=False)
Python
복사
데이터 로드
데이터 목록
•
survived
◦
생존 여부
◦
0이면 사망, 1이면 생존
•
pclass
◦
객실 등급
◦
1이면 1등급, 2이면 2등급, 3이면 3등급
•
sex
◦
성별
◦
male이면 남자, female이면 여자
•
age
◦
나이
•
sibsp
◦
함께 탑승한 형제 및 배우자 수
•
parch
◦
함께 탑승한 자녀 및 부모 수
•
fare
◦
요금
•
embarked
◦
탑승지 이름 앞글자
◦
C는 Cherbourg, Q는 Queenstown, S는 Southampton
•
class
◦
객실 등급
◦
First면 1등급, Second면 2등급, Third면 3등급
•
who
◦
남자, 여자, 아이
◦
man, woman, child
•
adult_male
◦
성인 남자인지 여부
◦
True면 성인 남자, False면 그외
•
deck
◦
선실 번호 첫 알파벳
◦
A, B, C, D, E, F, G
•
embark_town
◦
탑승지 이름
◦
Cherbourg, Queenstown, Southampton
•
alive
◦
생존여부
◦
no면 사망, yes면 생존
•
alone
◦
혼자 탑승했는지 여부
◦
True면 혼자 탑승, False면 가족과 함께 탑승
SEED = 42
df = sns.load_dataset('titanic')
print(df.shape)
# (891, 15)
Python
복사
데이터 확인
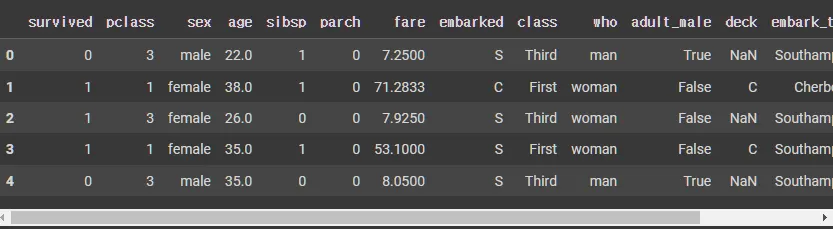
df.head()
Python
복사
타겟 데이터 확인
•
카테고리화 되어있을 때만 가능
new_survived = pd.Categorical(df["survived"])
new_survived[:5]
# [0, 1, 1, 1, 0]
# Categories (2, int64): [0, 1]
new_survived = pd.Categorical(df["survived"])
new_survived = new_survived.rename_categories(["Died","Survived"])
print(new_survived[:5])
# ['Died', 'Survived', 'Survived', 'Survived', 'Died']
# Categories (2, object): ['Died', 'Survived']
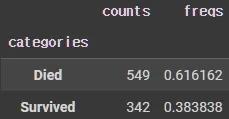
new_survived.describe()
Python
복사
데이터 분리
데이터 분리 라이브러리 모듈 import
from sklearn.model_selection import train_test_split
Python
복사
train, test 데이터 분리 tran_test_split
•
주요 파라미터
◦
X: 입력 데이터, 일반적으로 특징(feature) 배열
◦
y: 타겟 데이터, 일반적으로 레이블(label) 배열
◦
test_size
▪
테스트 세트의 비율이나 절대적 크기
▪
예를 들어 0.2는 전체 데이터의 20%를 테스트 세트로 사용하겠다는 의미
절대값으로도 설정 가능 (예: 1000).
◦
train_size
▪
훈련 세트의 비율이나 절대적 크기
▪
test_size와 동시에 사용하면 충돌할 수 있다.
◦
random_state
▪
난수 생성기의 시드(seed) 값
▪
데이터를 나누는 방식이 재현 가능하게 합니다. 같은 시드를 사용하면 동일한 데이터 분할을 얻을 수 있습니다.
◦
shuffle
▪
데이터를 분할하기 전에 섞을지 여부
▪
기본값은 True
▪
False로 설정하면 데이터가 섞이지 않는다.
◦
stratify
▪
클래스의 비율이 훈련 세트와 테스트 세트에 동일하도록 유지
▪
주로 불균형 클래스 문제를 다룰 때 유용
•
일반적으로 trainsize는 80~90, testsize는 20~10으로 잡고 진행
◦
학습량이 부족하면 testsize를 축소한다
X = df.drop('survived', axis=1) # 깊은 복사 -> 함수로 사용했을 때
y = df['survived'] # 얕은 복사 -> 함수가 아닐 떄
X_tr, X_te, y_tr, y_te = train_test_split(X, y, random_state=SEED, test_size = 0.2) # 20%를 테스트 데이터로 사용
X_tr = X_tr.reset_index(drop=True) # 인덱스를 초기화, drop=True를 하지 않으면 기존 인덱스가 새로운 열로 추가됨
X_te = X_te.reset_index(drop=True) # 인덱스를 초기화
X_tr.shape, X_te.shape
# ((712, 14), (179, 14))
Python
복사
◦
x는 피처만, y는 타겟만 넣어져있는 데이터
•
범주형 데이터만 추출
new_survived = pd.Categorical(y_tr) # y_tr을 범주형으로 변환
new_survived = new_survived.rename_categories(["Died","Survived"]) # 범주형 이름 변경
print(new_survived[:5]) # 5개만 출력
new_survived.describe() # 요약 통계 출력
Python
복사
Data Cleaning
•
데이터 분석 또는 머신러닝 프로젝트에서 데이터의 품질을 향상시키기 위해 수행하는 일련의 과정
•
데이터 수집, 변환, 저장 단계에서 발생할 수 있는 다양한 문제를 해결하는 데 중점
•
데이터를 올바르고 효율적으로 사용하기 위해서는 좋은 데이터를 사용해야합니다. 좋은 데이터는 완결성, 유일성, 통일성을 특정을 갖습니다.
하지만 항상 결측치 제거, 이상치 제거, 데이터 정규화 등을 하는 것이 좋은 것은 아니다.
모델이나 데이터 분포 또는 분석 목적에 따라 Data Cleaning을 하는 것이 좋다.
•
특성
◦
완결성 (Completeness)
데이터의 완결성은 데이터셋에 필요한 모든 정보가 포함되어 있는 정도를 의미
즉, 데이터셋에 누락된 값이나 불완전한 레코드가 없다는 것
문제:
▪
데이터 누락: 특정 열에 값이 없는 경우.
▪
불완전한 레코드: 중요한 정보가 빠진 경우.
해결 방법:
▪
결측치 처리: 결측치가 있는 경우 대체 방법(평균, 중앙값 등)이나 삭제 방법을 사용하여 처리
▪
데이터 검증: 데이터 입력 단계에서 유효성 검사를 통해 필수 정보가 모두 입력되도록 함
# 결측치가 있는 경우 대체하기
df.fillna(df.mean(), inplace=True)
# 결측치가 있는 행 제거하기
df.dropna(inplace=True)
Python
복사
◦
유일성 (Uniqueness)
유일성은 데이터셋 내의 레코드가 중복되지 않고, 각 레코드가 고유하게 식별될 수 있는 정도를 의미
유일한 식별자가 있어야 하는데, 이 식별자는 중복되지 않아야 함.
문제:
▪
중복 레코드: 데이터셋 내에 동일한 정보가 여러 번 포함되는 경우.
▪
비유일한 식별자: 레코드를 식별할 수 있는 값이 중복되는 경우.
해결 방법:
▪
중복 제거: 중복된 레코드를 식별하고 제거
▪
유니크 제약조건 설정: 데이터베이스 설계 시 유니크 제약조건을 설정하여 데이터의 유일성을 보장
# 중복된 행 제거하기
df = df.drop_duplicates()
# 특정 열의 유일성 검사하기
if df['ID'].duplicated().any():
print("중복된 ID가 있습니다.")
Python
복사
◦
통일성 (Consistency)
통일성은 데이터셋 내의 값들이 일관성 있게 정리되어 있는 정도를 의미
같은 데이터의 다양한 표현 방식이 충돌하지 않고 일관되게 유지되어야 함
문제:
▪
형식의 불일치: 날짜 형식이나 주소 형식이 서로 다른 경우.
▪
데이터의 불일치: 동일한 개체에 대해 서로 다른 정보가 기록된 경우.
해결 방법:
▪
데이터 형식 통일: 모든 데이터가 동일한 형식으로 정리되도록 변환
▪
데이터 정규화: 데이터의 형식을 표준화하여 일관되게 만듬
# 날짜 형식 통일하기
df['Date'] = pd.to_datetime(df['Date'])
# 문자열 데이터의 일관성 유지하기 (대문자 변환 등)
df['Category'] = df['Category'].str.upper()
Python
복사
중복 데이터 처리: df.drop_duplicates()
•
파라미터
◦
subset: 중복 검사를 할 열 또는 열들의 리스트. 기본값은 None으로, 모든 열을 기준으로 중복을 검사합니다.
◦
keep: 중복된 항목 중 어떤 항목을 유지할지 지정합니다.
▪
'first': 첫 번째 항목만 유지.
▪
'last': 마지막 항목만 유지.
▪
False: 모든 중복 항목을 제거.
◦
inplace: 원본 DataFrame에서 중복을 제거할지 여부.
▪
True: 원본 DataFrame을 수정하고 새로운 DataFrame을 반환하지 않음.
▪
False: 새로운 DataFrame을 반환하고 원본은 변경하지 않음 (기본값).
# 중복제거
print(f'before: {df.shape}')
df.drop_duplicates(keep='first', inplace=True, ignore_index=True)
print(f'after: {df.shape}')
# before: (891, 15)
# after: (784, 15)
Python
복사
결측치(Missing Value) - Train Data만 확인
테스트 데이터로 결측치를 채우면 탈락
•
데이터셋에서 특정 데이터가 누락된 상태를 의미
•
값이 없는 것
•
표현 방식
◦
NaN: Not a Number (숫자가 아닌)
◦
Null: 아무것도 존재하지 않음
◦
undefined: 정의되어 있지 않음
0은 데이터가 있으므로 결측치가 아님!
결측치 유형 파악
완전 무작위 결측(MCAR: Missing Completely At Random)
결측치가 데이터의 다른 값들과 전혀 관련이 없고, 결측 여부가 무작위로 발생하는 것
⇒ 결측치가 완전히 무작위로 발생하고, 다른 데이터와는 관계가 없다.
•
X1, X2, X3라는 특성이 있다고 가정할 때, X2열의 결측치가 X1, X2, X3 열의 다른 값들과 아무런 상관관계가 없을 경우, 이를 완전 무작위 결측이라고 한다.
•
대부분의 결측치 처리 패키지는 이러한 유형의 결측치를 대상으로 하고 있으며, 데이터를 입력한 이가 실수를 했거나, 전상상의 에러가 난 경우이다.
무작위 결측(MAR: Missing At Random)
결측치가 데이터의 다른 값들과는 관계가 없지만, 결측 여부가 다른 관측 가능한 변수와 관련있는 것
⇒ 결측치가 다른 관측 가능한 변수와는 관련이 있지만, 결측 여부 자체는 무작위이다.
•
X1, X2, X3라는 특성이 있다고 가정할 때, X1이 True인 경우, X2는 결측치를 갖고, X1이 False인 경우, X2는 값을 가진다면,
•
다시 말해 다른 특성의 값에 따라 결측치의 발생 확률이 계산된다면, 그러나 값자체의 상관관계는 알 수 없는 경우. 이를 무작위 결측이라고 한다.
비무작위 결측(NMAR: Not Missing At Random)
결측치가 데이터의 다른 값들과 직접적으로 연관이 있으며, 결측 여부가 관측된 값에 의해 설명될 수 있는 것
⇒ 결측치가 데이터의 다른 값과 직접적인 관계가 있다. 즉, 결측 여부가 데이터 값에 따라 달라진다.
•
위의 두가지 유형이 아닐 때, 비무작위 결측이라 지칭.
•
이 경우 결측치가 일어난 특성(X2)의 값이 다른 특성(X1)의 값과 상관관계가 있다.
예제
예) 성별(X)을 사용해 체중(y)을 예측하는 모델을 구축하기 위해, 설문조사를 통해 Xy DataFrame을 구성했는데, y열에 결측치가 있다고 가정할 떄
•
완전 무작위 결측
단순히 그냥. 체중을 응답하지 않았던 경우
즉, y가 누락된 이유는 다른 X, y값들과는 관련이 없다.
•
무작위 결측
여성(X)의 경우 체중에 잘 응답하지 않았던 경우
즉, y가 누락된 것은 성별(X)에 영향을 받는다.
•
비무작위 결측
체중이 무거운 사람들은 자신의 체중을 잘 응답하지 않는다.
즉, y가 누락된 것은 y자체에 영향을 받았다.
결측치 탐색
통계 탐색
X_tr.info() # info()를 통해서 확인 가능
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 712 entries, 0 to 711
Data columns (total 14 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 pclass 712 non-null int64
1 sex 712 non-null object
2 age 572 non-null float64
3 sibsp 712 non-null int64
4 parch 712 non-null int64
5 fare 712 non-null float64
6 embarked 710 non-null object
7 class 712 non-null category
8 who 712 non-null object
9 adult_male 712 non-null bool
10 deck 158 non-null category
11 embark_town 710 non-null object
12 alive 712 non-null object
13 alone 712 non-null bool
dtypes: bool(2), category(2), float64(2), int64(3), object(5)
memory usage: 59.0+ KB
Python
복사
•
전체 결측치 수 .sort_values(ascending=False)로 항상 정렬을 해서 봐야한다.
X_tr.isnull().sum().sum() # 전체 결측치 수
# 698
---------------------------------------------------------------------------
X_tr.isnull().sum().sort_values(ascending=False) # 각 컬럼별 결측치 수
# return
deck 554
age 140
embarked 2
embark_town 2
pclass 0
sex 0
sibsp 0
parch 0
fare 0
class 0
who 0
adult_male 0
alive 0
alone 0
dtype: int64
---------------------------------------------------------------------------
(X_tr.isnull().sum() / X_tr.shape[0]).round(4).sort_values(ascending=False) # 각 걸럼별 결측치 비율
# return
deck 0.7781
age 0.1966
embarked 0.0028
embark_town 0.0028
pclass 0.0000
sex 0.0000
sibsp 0.0000
parch 0.0000
fare 0.0000
class 0.0000
who 0.0000
adult_male 0.0000
alive 0.0000
alone 0.0000
dtype: float64
Python
복사
그래프 탐색
•
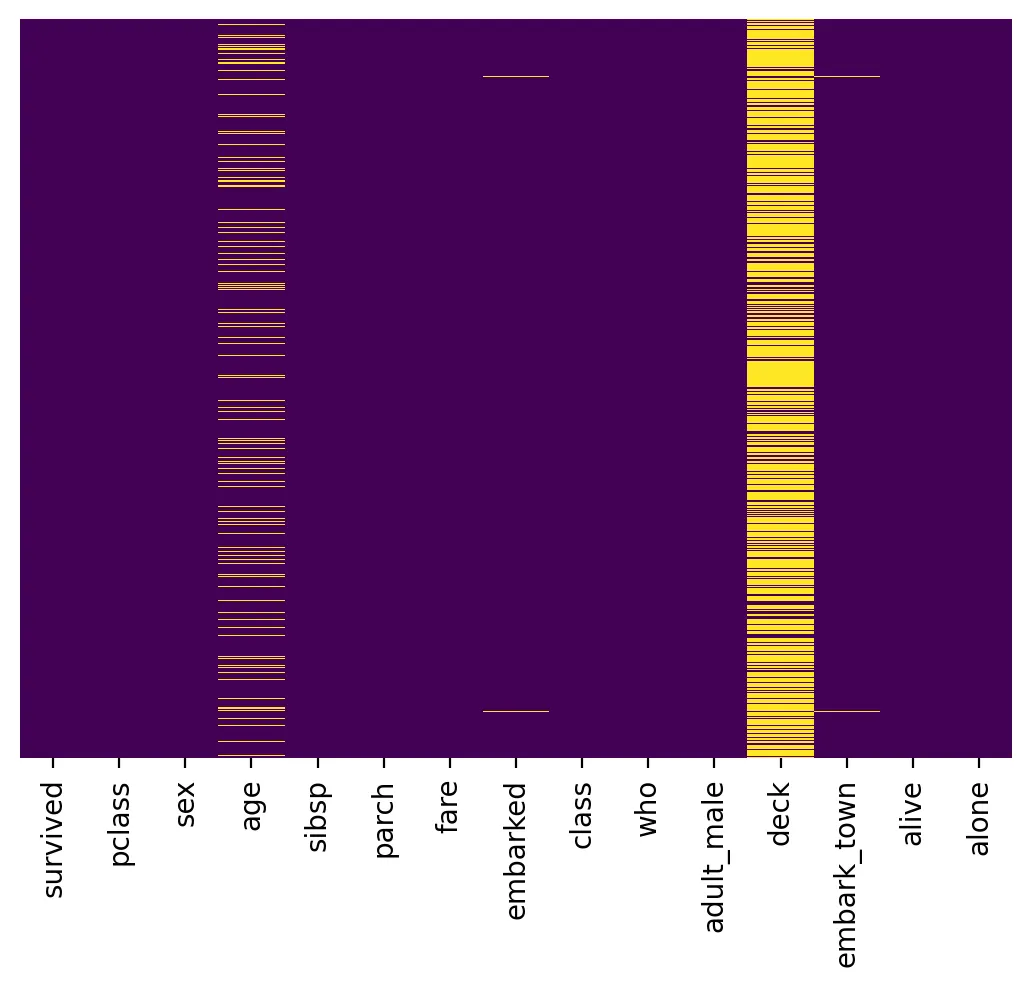
히트맵
# checking null values using the heatmap for better results
# 결측치 시각화 (결측치가 많을 수록 색이 진한 것을 확인 가능)
sns.heatmap(df.isnull(), yticklabels = False, cbar = False, cmap = 'viridis')
# heatmap 파라미터
# 히트맵에 사용할 데이터 - df.isnull로 결측치 여부를 나타냄
# true는 결측치가 있는 위치
# false는 결측치가 없는 위치
# yticklabels : y축 레이블 표시 여부
# cbar(color bar) : 컬러바 표시 여부
# cmap(color map) : 컬러맵
# viridis는 색상의 스펙트럼을 제공하는 색상 맵
# 결측치가 있는 위치와 없는 위치를 색상으로 구분
Python
복사
•
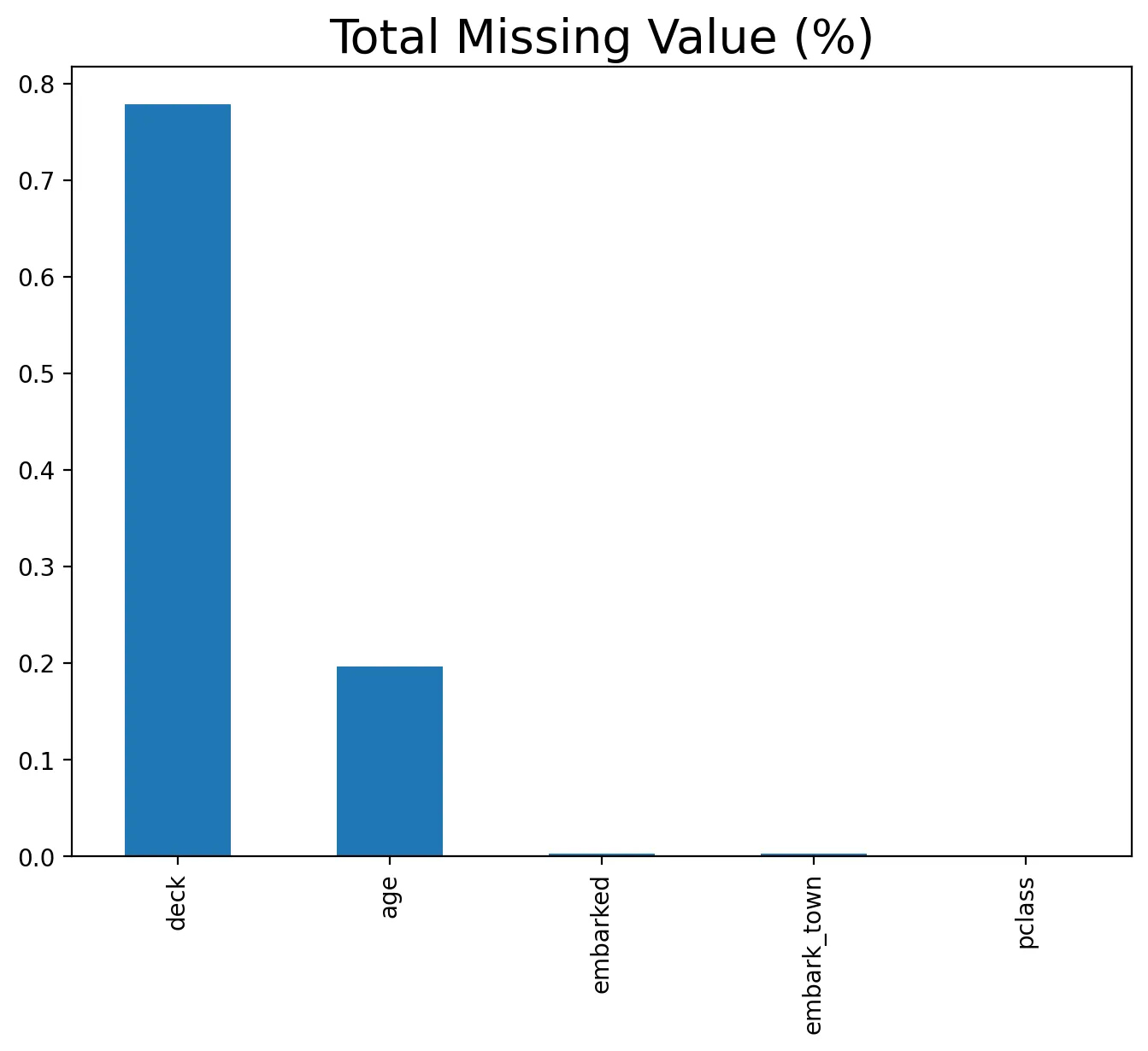
총합 결측치 비율
# 데이터프레임 X_tr의 각 열에 대해 결측치의 총합을 계산한 후, 이를 내림차순으로 정렬
total = X_tr.isnull().sum().sort_values(ascending=False)
# 각 열의 결측치 비율을 계산하고 이를 내림차순으로 정렬
percent = (X_tr.isnull().sum()/X_tr.isnull().count()).sort_values(ascending=False)
# X_tr.isnull().count(): 각 열의 전체 데이터 수를 반환
# X_tr.isnull().sum() / X_tr.isnull().count(): 결측치 개수를 전체 데이터 수로 나누어 결측치 비율을 계산
# sort_values(ascending=False): 비율을 내림차순으로 정렬, 높은 열이 위로
# missing_data = pd.concat([total, percent], axis=1, keys=['Total', 'Percent'])
percent_data = percent.head()
# 상위 결측치 비율 데이터를 막대 그래프로 시각화
percent_data.plot(kind="bar", figsize = (8,6), fontsize = 10)
# kind="bar": 막대 그래프를 생성
# figsize=(8, 6): 그래프의 크기를 설정 (너비 8인치, 높이 6인치).
# fontsize=10: 축 레이블과 그래프 제목의 글꼴 크기를 설정
# x축의 레이블을 설정
plt.xlabel("", fontsize = 20)
# y축의 레이블을 설정
plt.ylabel("", fontsize = 20)
# 그래프의 제목 설정
plt.title("Total Missing Value (%)", fontsize = 20)
# 그래프 표시
plt.show()
Python
복사
•
box그래프
# deck 열의 결측치 여부를 기반으로 새로운 열 hasDeck을 생성
X_tr['hasDeck'] = X_tr['deck'].isnull().apply(lambda x: 0 if x == True else 1)
# X_tr['deck'].isnull(): deck 열의 각 값이 결측치인지 여부를 Boolean 값으로 반환
# age 열의 결측치 여부를 기반으로 새로운 열 hasAge을 생성
X_tr['hasAge'] = X_tr['age'].isnull().apply(lambda x: 0 if x == True else 1)
# X_tr['age'].isnull(): age 열의 각 값이 결측치인지 여부를 Boolean 값으로 반환
# apply(lambda x: 0 if x == True else 1): Boolean 값(True 또는 False)을 0 또는 1로 변환
Python
복사
# fare 열과 hasDeck 열을 합쳐서 새로운 데이터프레임 data를 생성
data = pd.concat([X_tr['fare'], X_tr['hasDeck']], axis=1)
# 열을 기준으로 데이터프레임을 결합
# 즉, fare와 hasDeck이 같은 행 인덱스를 가지며 나란히 배치
# 그래프의 크기를 설정
f, ax = plt.subplots(figsize=(8, 6))
# plt.subplots(): 새로운 그림 객체(f)와 축 객체(ax)를 생성
# 박스 플롯 시각화
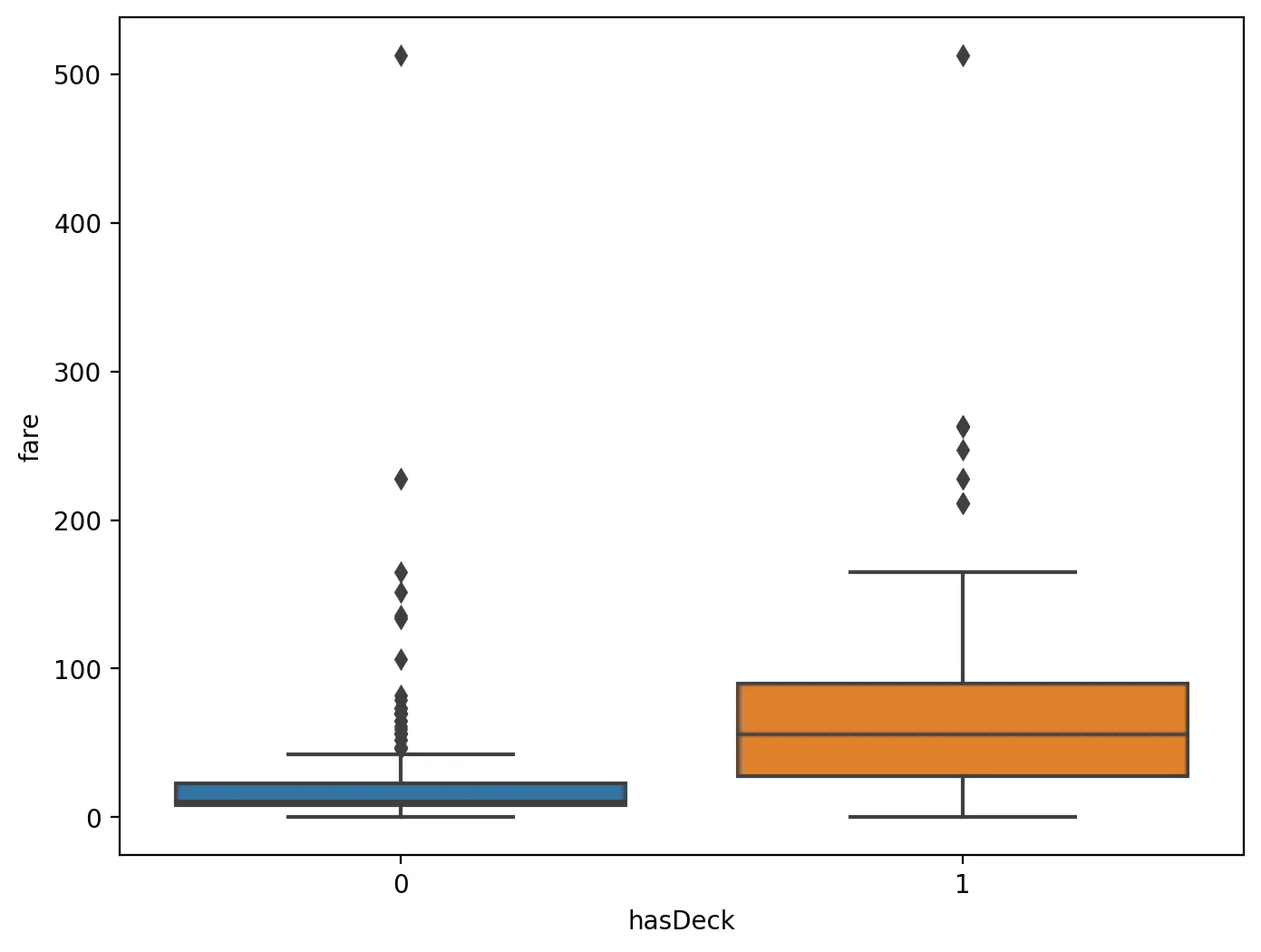
fig = sns.boxplot(x='hasDeck', y="fare", data=data)
# data=data: 시각화할 데이터프레임을 지정
Python
복사
◦
cabin(deck)의 값이 있는 사람들이 fare가 높은 경향이 있다.
•
mosaic
from statsmodels.graphics.mosaicplot import mosaic
# 모자이크 플롯 생성
# 범주형 데이터를 시각화할 수 있는 함수로, 교차 분포를 모자이크 플롯으로 표현
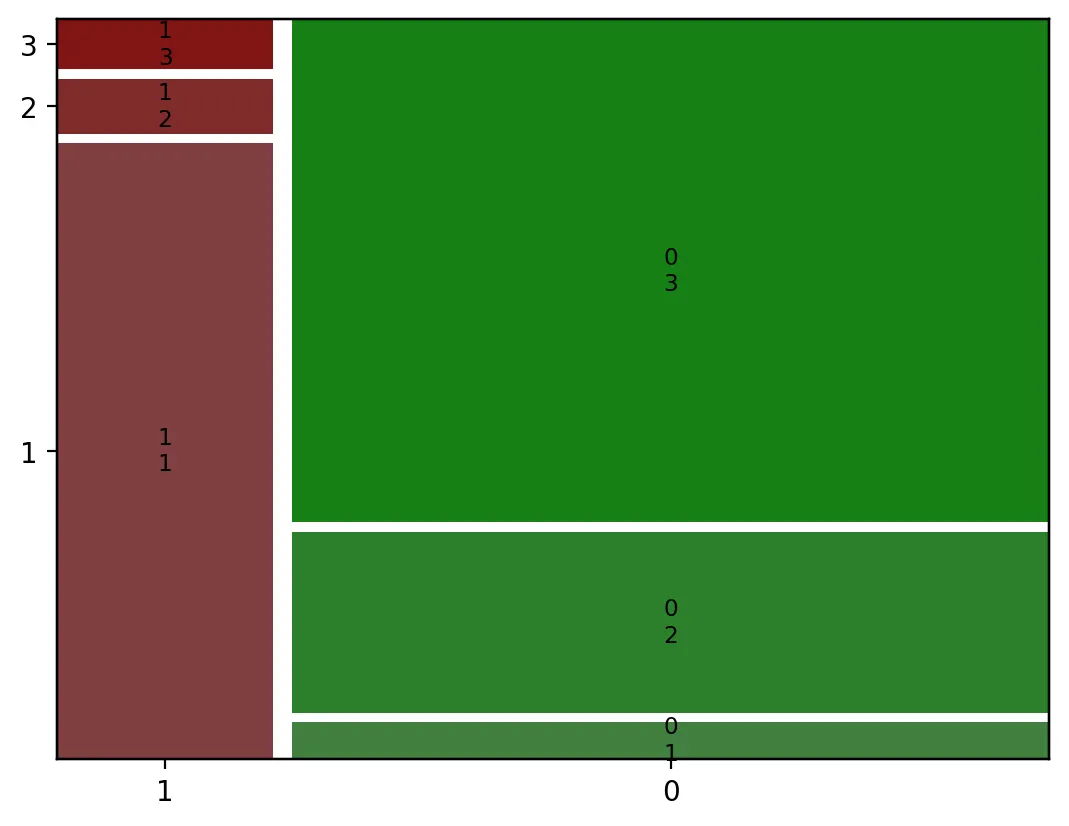
mosaic(X_tr, ['hasDeck', 'pclass'],gap=0.02)
# X_tr: 모자이크 플롯을 생성할 데이터프레임
# ['hasDeck', 'pclass']: 시각화할 두 개의 범주형 변수
# hasDeck과 pclass 변수 간의 교차 분포를 시각화
# gap=0.02: 모자이크 플롯에서 사각형 사이의 간격을 설정. 값이 0.02로 설정
# 각 사각형 간의 간격을 조정
plt.show()
Python
복사
가로축(X): 첫 번째 범주형 변수의 값.
세로축(y): 두 번째 범주형 변수의 값.
사각형 크기: 두 범주형 변수의 조합에 해당하는 빈도 또는 비율을 시각적으로 표현
◦
위의 그래프를 보면 pclass가 3 > 2 > 1 순으로 hasCabin이 0일 확률이 높다.
◦
즉, pclass가 1이면 Cabin값이 null이 아닐 확률이 높다는 뜻이다.
•
concat, subplots, boxplot
# X_tr 데이터프레임에서 fare 열과 embarked 열을 선택하여 새로운 데이터프레임 data를 생성
data = pd.concat([X_tr['fare'], X_tr['embarked']], axis=1)
# pd.concat([X_tr['fare'], X_tr['embarked']], axis=1): 두 열을 열 방향(axis=1)으로 결합
# fare와 embarked가 함께 포함된 데이터프레임이 생성
# 박스 플롯을 그릴 그림 객체(f)와 축 객체(ax)를 생성
# figsize=(너비, 높이)는 그림의 크기를 설정
f, ax = plt.subplots(figsize=(8, 6))
# 박스 플롯을 생성
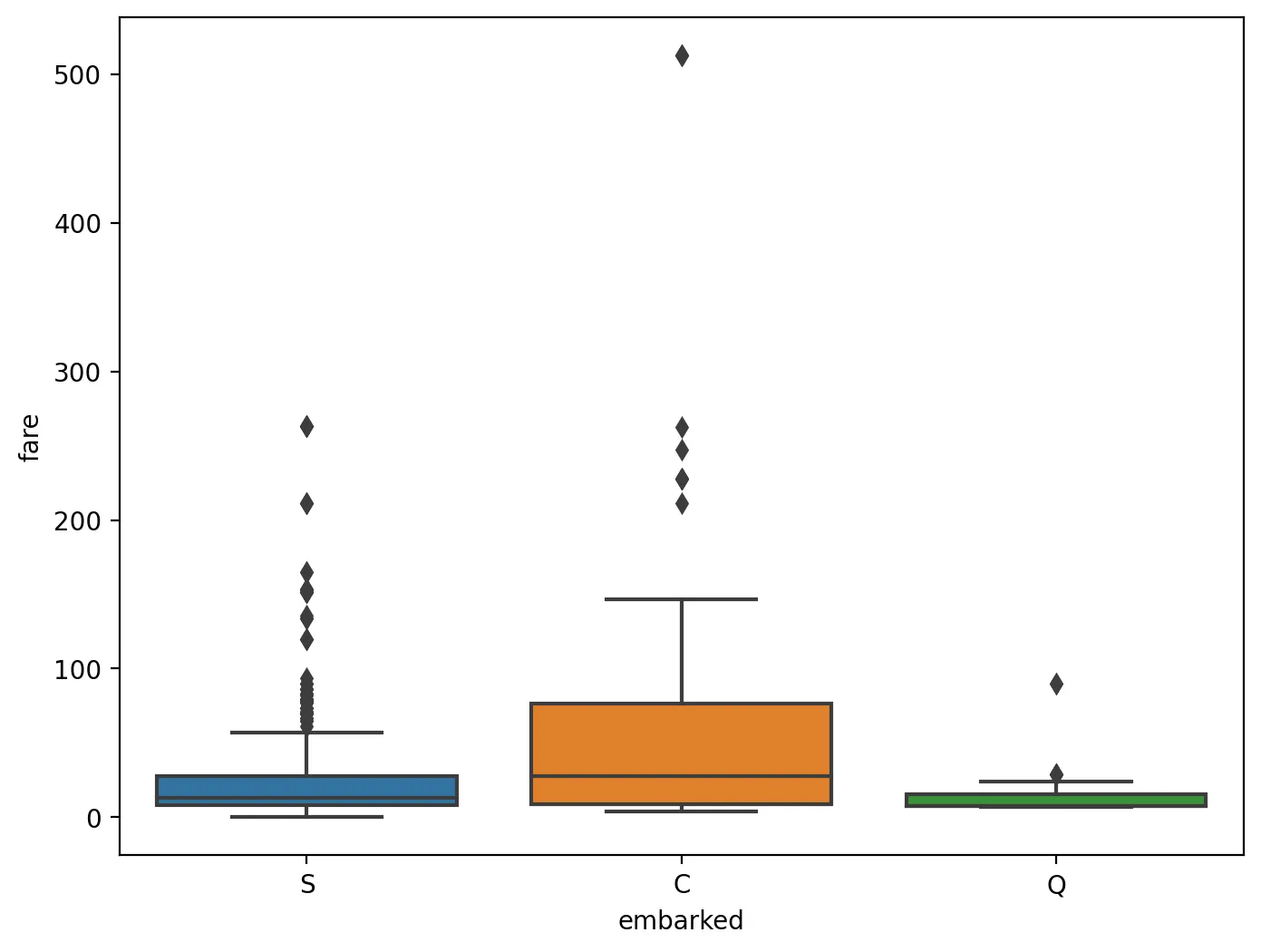
fig = sns.boxplot(x='embarked', y="fare", data=data)
# x축에 embarked 열의 값을 사용합니다. embarked는 범주형 변수로, 이 값에 따라 fare의 분포가 그룹화
# x='embarked': x축에 embarked 열의 값을 사용합니다.
# embarked는 범주형 변수로, 이 값에 따라 fare의 분포가 그룹화
# y='fare': y축에 fare 열의 값을 사용합니다. fare는 연속형 변수
# 각 embarked 값에 대한 요금 분포를 표시
# 시각화할 데이터프레임을 지정
Python
복사
박스 플롯
중앙값 (Median)
•
박스의 중앙에 위치한 선, 데이터의 중간값
•
데이터의 50%가 이 값보다 작고 나머지 50%가 이 값보다 크다.
사분위수 (Quartiles)
•
1사분위수 (Q1): 데이터의 하위 25%에 해당하는 값, 박스의 하단 경계선
•
3사분위수 (Q3): 데이터의 상위 25%에 해당하는 값, 박스의 상단 경계선
•
박스의 높이는 Q1과 Q3 사이의 범위
사분위 범위 (Interquartile Range, IQR)
•
Q3 - Q1의 값, 데이터의 중앙 50% 범위를 나타내며, 박스의 높이에 해당
•
IQR은 데이터의 분포와 변동성을 이해하는 데 중요한 지표
수염 (Whiskers)
•
박스의 상단과 하단에서 중앙값까지의 범위
•
일반적으로 수염의 길이는 IQR의 1.5배까지로 설정, 이 범위를 벗어나는 값은 이상치로 간주
•
수염의 끝은 데이터의 최대값과 최소값(이상치를 제외한 경우).
이상치 (Outliers)
•
박스와 수염의 범위를 벗어나는 데이터 포인트
•
이상치는 일반적으로 박스 플롯에서 점으로 표시
•
위의 그래프를 보면 embarked는 C > S > Q 순으로 fare가 높은 경향이 있다.
•
subplots, boxplot
# 새로운 그림 객체(f)와 축 객체(ax)를 생성
f, ax = plt.subplots(figsize=(8, 6))
# 박스 플롯을 생성
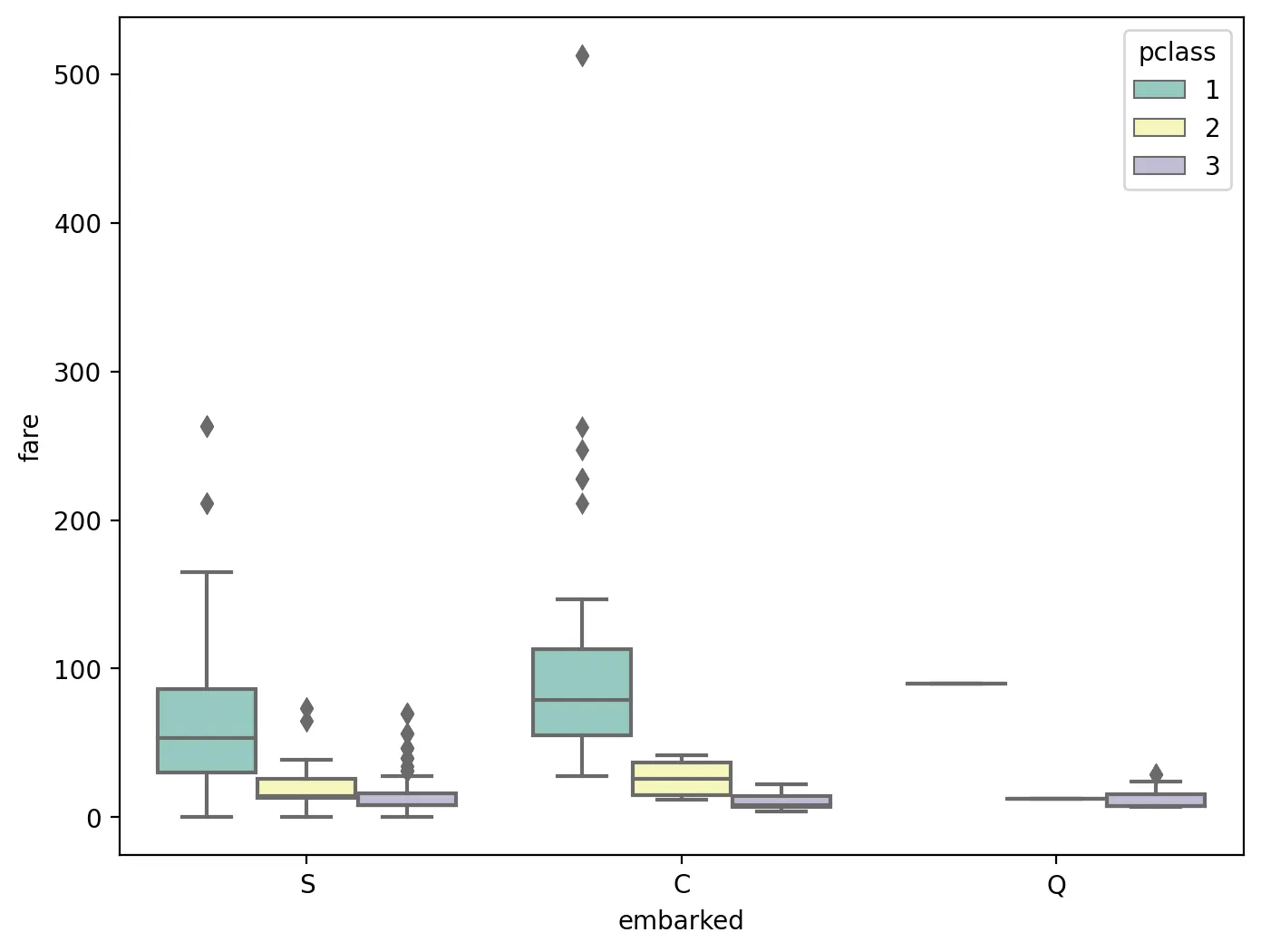
sns.boxplot(x="embarked", y="fare", hue="pclass",
data=X_tr, palette="Set3")
# x="embarked": x축에 embarked 열의 값을 설정
# 범주형 변수로, 탑승한 항구를 표시
# y="fare": y축에 fare 열의 값을 설정
# 승객의 요금을 나타내는 연속형 변수
# hue="pclass": pclass 열의 값에 따라 색상을 구분
# hue는 데이터의 추가적인 범주형 변수를 색상으로 구분할 때 사용
# 여기서는 pclass(탑승 클래스)에 따라 색상을 다르게 하여 각 클래스의 fare 분포를 비교
# data=X_tr: 박스 플롯에 사용할 데이터프레임을 지정
# palette="Set3": 색상 팔레트를 설정
# "Set3"은 Seaborn에서 제공하는 색상 팔레트 중 하나
# 서로 다른 색상을 사용하여 pclass의 각 값을 구분
Python
복사
◦
위 그래프를 보면 embarked(C > S > Q)와 pclass (1 > 2 > 3)을 같이 적용하면, 더욱더 fare가 높은 경향을 보인다.
결측치 구간화
•
연속형 데이터를 범주형 데이터로 변경하면서 처리하는 기법
•
히스토그램 방식의 binning을 사용하여 인코딩을 하면 결측치를 없애지 않고 사용할 수 있다.
•
예를 들어 나이에 결측치가 많다면 나이가 적음, 중간, 많음 또는 10대, 20대, ... 80대 이상으로 구간화를 할 수 있다.
•
구간화를 하고 인코딩을 하면 결측치를 따로 채우지 않아도 되기 때문에 정보의 왜곡을 줄여 과대적합도 방지절대평가(pd.cut) vs 상대평가(pd.qcut)
절대평가(pd.cut) vs 상대평가(pd.qcut)
•
절대평가
tmp_train['age_cut'] = pd.cut(tmp_train['age'].values, bins=4, labels=list(range(1,5)))
print(tmp_train['age_cut'].value_counts())
Python
복사
•
상대평가
tmp_train['age_qcut'] = pd.qcut(tmp_train['age'].values, q=4, labels=list(range(1,5)))
print(tmp_train['age_qcut'].value_counts())
Python
복사
•
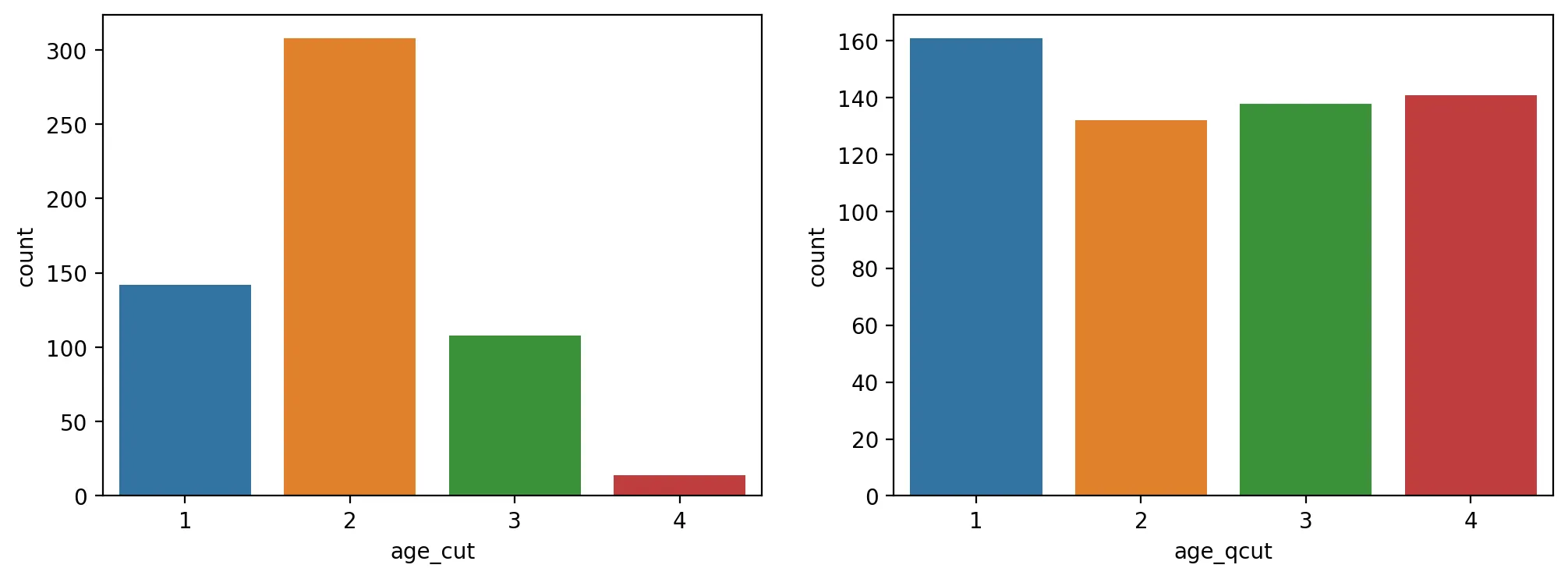
그래프
fig, axes = plt.subplots(1,2, figsize=(12,4))
sns.countplot(data=tmp_train, x='age_cut', ax=axes[0])
sns.countplot(data=tmp_train, x='age_qcut', ax=axes[1])
Python
복사
결측치 처리
•
제거
◦
결측치가 발생한 행 또는 열을 삭제해버리는 가장 쉽고, 단순한 방식이다.
◦
그러나 당연하게도 이런 방식은 데이터의 손실(=표본 크기의 축소)로 이어집니다. 또한 경우에 따라 결측값을 무시하고 관측치만으로 분석을 시행할 경우 통계적 편향이 생길 가능성이 커지기에 조심히 시행되어야 합니다.
•
치환(합리적 접근)
◦
말 그대로 결측치를 적당한 방법으로 대체하는 것입니다.
◦
데이터의 특성에 맞게 적당한 평균, 중간값, 최빈값 등으로 채울 수도 있으며, 다른 특성과 상관관계가 있을 경우 그에 맞는 값을 넣어 줄 수도 있습니다.(그러나 평균값 등으로 단순 대체하는 방법은 자료의 편향성을 높이고 특성들간의 상관관계를 왜곡할 수 있는 가장 안좋은 방법입니다.)
◦
가령 월급특성에 결측치가 있는데, 연봉특성에는 값이 있는 경우 월급 결측치를 채우는 것이 수월할 것입니다. 이런 합리적 접근을 통한 치환 방법은 데이터에 대한 어느 정도의 도메인 지식이 있는 경우 굉장히 효율적으로, 그리고 정확하게 작동할 수 있습니다.
•
모델 기반 처리
◦
결측치를 예측하는 새로운 모델을 구성하고, 이를 기반으로 결측치를 채워나가는 방식입니다.
◦
변수의 특성에 따라 Knn, PolyRegression 등의 방법을 시행할 수도 있습니다.
pandas 사용 결측치 처리
•
메서드들
◦
df.dropna()
▪
df.dropna(axis=0): row 삭제
▪
df.dropna(axis=1): column 삭제
▪
df[['컬럼명']].dropna(axis=1): column 삭제
▪
df.dropna(subset=['원하는 행']): 원하는 행의 결측값이 있는 부분을 기준으로 row 삭제
◦
df.fillna()
▪
df[['컬럼명']].fillna(원하는 값): 원하는 값으로 채우기
▪
df[['컬럼명']].fillna(method='ffill'): 결측값을 앞방향의 값으로 채운다.
▪
df[['컬럼명']].fillna(method='bfill'): 결측값을 뒤방향의 값으로 채운다.
◦
np.where(pd.notnull(df['null값보유컬럼']==True, df['null값보유컬럼],df['null값없는컬럼'])
◦
df.replace()
▪
list_df.replace(np.nan, 5): 결측값을 5로 변경
▪
df.replace({'원하는 column 명' : 바꾸고싶은값}, {'원하는 column 명' : 새로운값})
◦
df.interpolate(method = 'values')
결측값을 선형으로 비례하는 방식으로 결측값 보간 =적절한 비율의 값으로 보간
◦
apply()
# lambda 함수 만들고 apply
fill_mean_func = lambda x: x.fillna(x.mean())
df.groupby('그룹하고싶은컬럼').apply(fill_mean_func)
Python
복사
# 특정값 지정은 dict형식으로 한다 그룹화 한 값 'a', 'b'의 그룹에 채울 새로운값 지정
fill_values = {'a': 1.0, 'b':0.5}
# lambda 함수 지정
fill_func = lambda x: x.fillna(fill_values[x.name])
df.group('그룹화할col명').apply(fill_func)
Python
복사
•
행 제거 방법 (.dropna(axis=0))
print(f'before: {X_tr.shape} / isnull().sum(): {X_tr.isnull().sum().sum()}')
# 결측치가 있는 행 제거 : X_tr.dropna(axis=0)
df_droprows = X_tr.dropna(axis=0)
print(f'after: {df_droprows.shape} / isnull().sum(): {df_droprows.isnull().sum().sum()}')
# before: (712, 16) / isnull().sum(): 698
# after: (142, 16) / isnull().sum(): 0
Python
복사
•
열 제거 방법 (.dropna(axis=1)) (결측치가 있는 열 제거)
print(f'before: {X_tr.shape} / isnull().sum(): {X_tr.isnull().sum().sum()}')
# 결측치가 있는 열 제거 : X_tr.dropna(axis=1)
df_dropcols = X_tr.dropna(axis=1)
print(f'after: {df_dropcols.shape} / isnull().sum(): {df_dropcols.isnull().sum().sum()}')
# before: (712, 16) / isnull().sum(): 698
# after: (712, 12) / isnull().sum(): 0
Python
복사
•
수치형 치환 (추천하는 방법)
X_tr['age_mean'] = X_tr['age'].fillna(X_tr['age'].mean())
X_tr['age_median'] = X_tr['age'].fillna(X_tr['age'].median())
X_tr[['age_mean', 'age_median']].isnull().sum().sum()
# 0
# ---------------------------------------------------
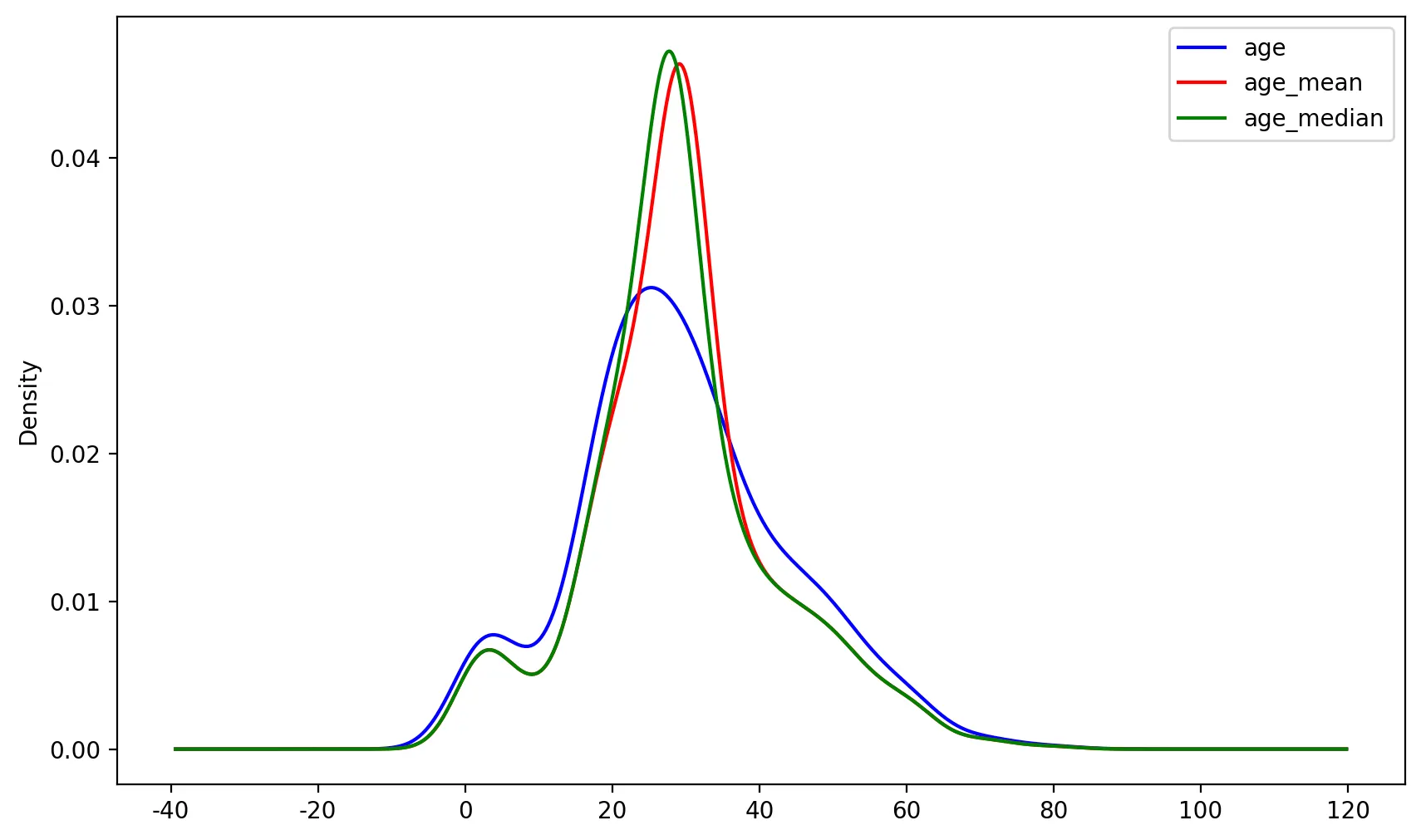
# 분포 시각화
fig, ax = plt.subplots(figsize=(10,6))
X_tr['age'].plot(kind='kde', ax=ax, color='blue')
X_tr['age_mean'].plot(kind='kde', ax=ax, color='red')
X_tr['age_median'].plot(kind='kde', ax=ax, color='green')
lines, labels = ax.get_legend_handles_labels()
ax.legend(lines, labels, loc='best')
Python
복사
X_te['age_mean'] = X_te['age'].fillna(X_tr['age'].mean())
X_te['age_median'] = X_te['age'].fillna(X_tr['age'].median())
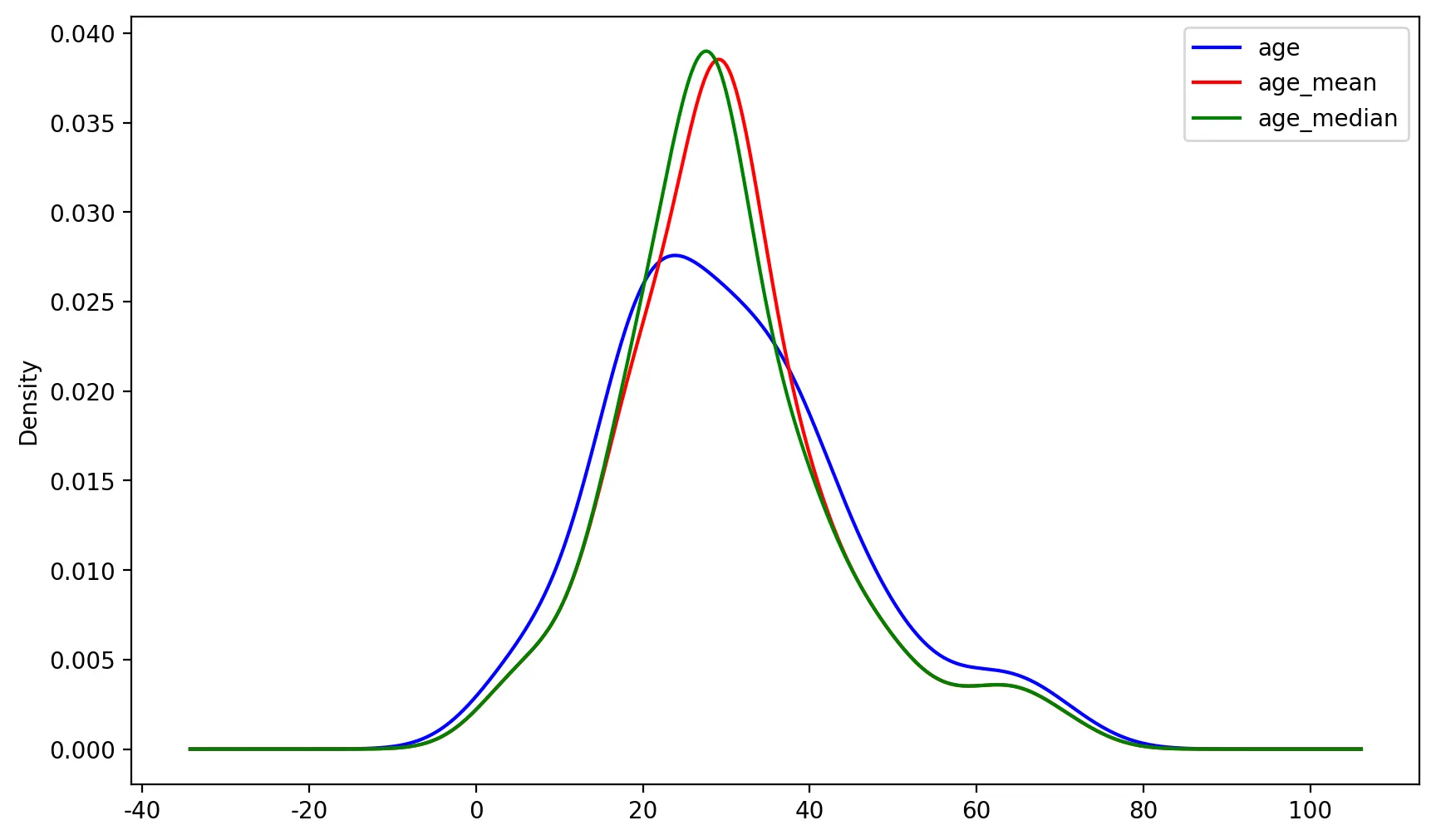
# 분포 시각화
fig, ax = plt.subplots(figsize=(10,6))
X_te['age'].plot(kind='kde', ax=ax, color='blue')
X_te['age_mean'].plot(kind='kde', ax=ax, color='red')
X_te['age_median'].plot(kind='kde', ax=ax, color='green')
lines, labels = ax.get_legend_handles_labels()
ax.legend(lines, labels, loc='best')
Python
복사
◦
위의 그래프는 원래의 분포와 mean/median 분포가 다른 것을 볼 수 있다.
◦
즉, 단순 mean/median으로 결측치 처리를 하면 기존 데이터의 분포가 변형이 된다는 것을 확인할 수 있다.
X_te['age_random'] = X_te['age']
# random sampling
random_sampling = (X_tr['age'].dropna().sample(X_te['age'].isnull().sum()))
random_sampling.index = X_te[lambda x: x['age'].isnull()].index # index 부여
# NA imputation
X_te.loc[X_te['age'].isnull(), 'age_random'] = random_sampling
# 확인
print(X_te[['age', 'age_random']].isnull().sum())
Python
복사
# 분포 시각화
fig, ax = plt.subplots(figsize=(10,6))
X_te['age'].plot(kind='kde', ax=ax, color='blue')
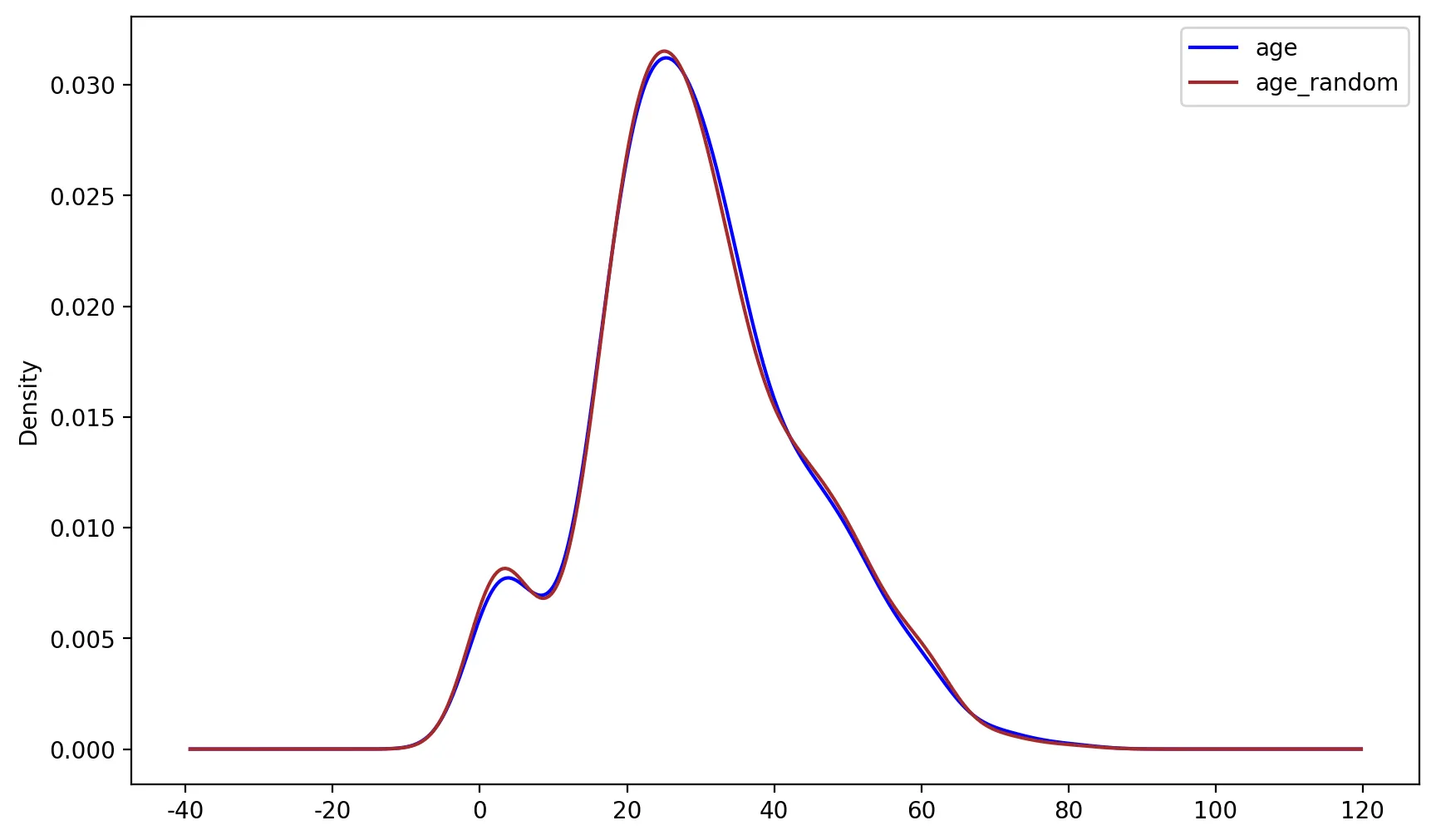
X_te['age_random'].plot(kind='kde', ax=ax, color='brown')
lines, labels = ax.get_legend_handles_labels()
ax.legend(lines, labels, loc='best')
Python
복사
# 먼저 'age_random'이라는 새로운 열을 만드는데, 이는 'age' 열의 복사본
# 이 열은 결측치를 채운 후의 값을 저장할 것
X_te['age_random'] = X_te['age']
# random sampling : 샘플링을 수행
random_sampling = (X_tr['age'].dropna().sample(X_te['age'].isnull().sum()))
# X_tr['age'].dropna(): X_tr 데이터프레임의 age 열에서 결측치가 없는 값들만을 선택
# .sample(X_te['age'].isnull().sum()): X_te의 age 열에서 결측치가 있는 행의 수만큼 무작위로 값을 선택
random_sampling.index = X_te[lambda x: x['age'].isnull()].index # index 부여
# random_sampling.index = X_te[lambda x: x['age'].isnull()].index: X_te의 age 열에서 결측치가 있는 위치(행)의 인덱스를 random_sampling의 인덱스로 설정하여, 샘플링된 값들이 해당 결측치 위치에 정확하게 할당될 수 있도록 함
# NA imputation
X_te.loc[X_te['age'].isnull(), 'age_random'] = random_sampling
# X_te 데이터프레임의 age 열에서 결측치가 있는 위치에, 앞서 샘플링된 값을 age_random 열에 채워 넣는다. 이를 통해 결측치를 대체
# 확인
print(X_te[['age', 'age_random']].isnull().sum())
age 37
age_random 0
dtype: int64
<matplotlib.legend.Legend at 0x7e6f5f71f640>
Python
복사
# 분포 시각화
fig, ax = plt.subplots(figsize=(10,6))
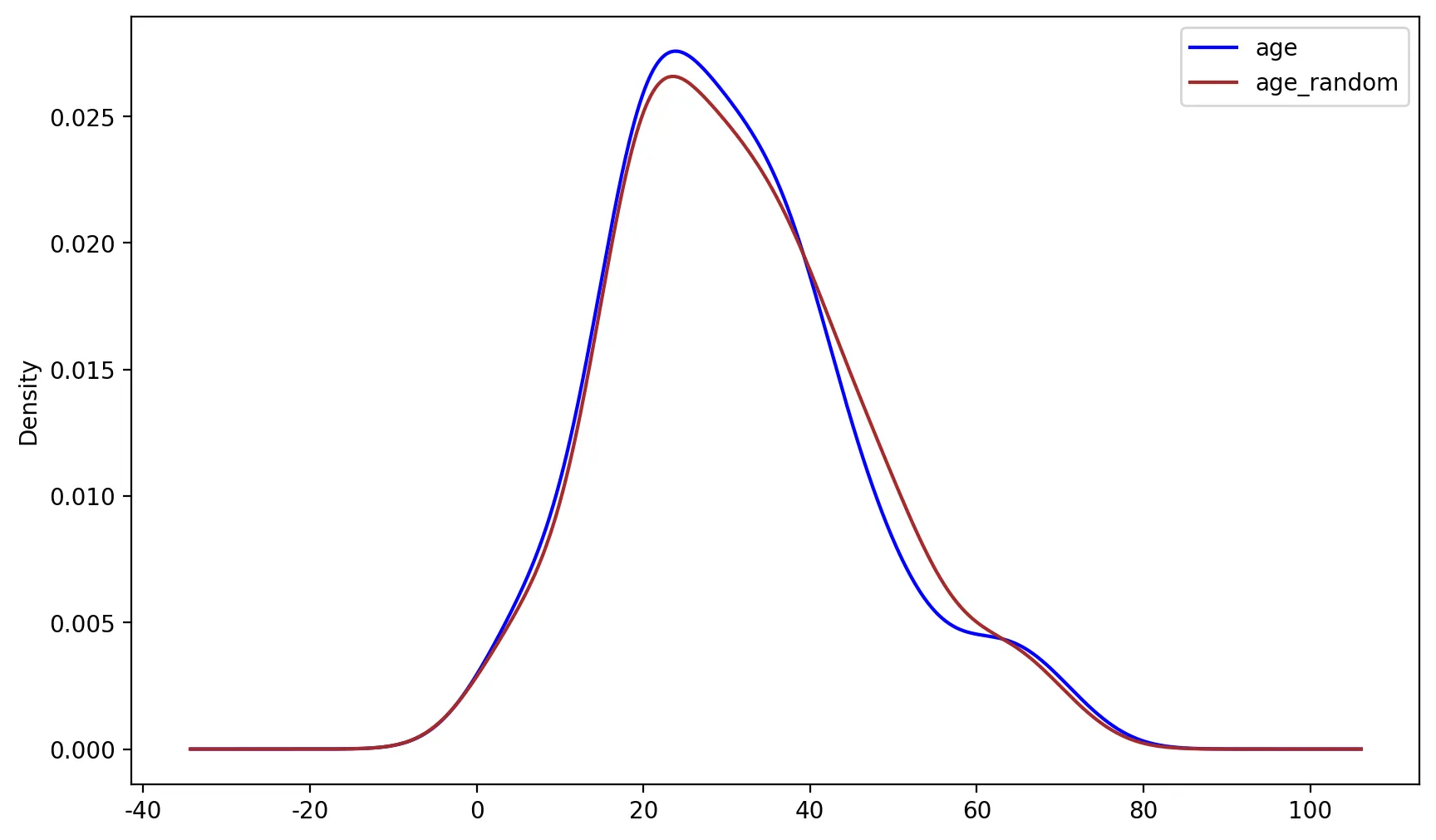
X_te['age'].plot(kind='kde', ax=ax, color='blue')
X_te['age_random'].plot(kind='kde', ax=ax, color='brown')
lines, labels = ax.get_legend_handles_labels()
ax.legend(lines, labels, loc='best')
Python
복사
◦
위의 그래프를 보면 mean/median과 달리 random sample imputation의 경우 원래의 분산 및 분포를 보존한다는 장점을 확인할 수 있다.
•
범주형 치환
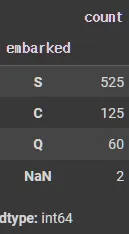
# 범주 별 빈도 수 확인
X_tr['embarked'].value_counts(dropna=False)
Python
복사
X_tr['age'].isnull().sum()
# 140
embarked_mode = X_tr['embarked'].mode().values[0]
embarked_mode
# 'S'
Python
복사
# 최빈값 (가장 자주 등장하는 값)
embarked_mode = X_tr['embarked'].mode().values[0]
# NA imputation
# X_tr와 X_te 데이터프레임의 embarked 열에서 결측치를 최빈값(embarked_mode)으로 채운다.
X_tr['embarked_filled'] = X_tr['embarked'].fillna(embarked_mode)
X_te['embarked_filled'] = X_te['embarked'].fillna(embarked_mode)
# .fillna(embarked_mode): embarked 열에서 결측치(NaN)를 embarked_mode로 대체
# X_tr['embarked_filled']와 X_te['embarked_filled']라는 새로운 열을 만들어 결측치가 채워진 결과를 저장
# 확인
print(X_tr[['embarked', 'embarked_filled']].isnull().sum())
print('-'*50)
print(X_te[['embarked', 'embarked_filled']].isnull().sum())
# isnull().sum(): 각 열에 있는 결측치의 총 개수를 계산
# X_tr와 X_te 각각에 대해 embarked 열과 embarked_filled 열을 비교하여 결측치가 제대로 처리되었는지 확인
embarked 2
embarked_filled 0
dtype: int64
--------------------------------------------------
embarked 0
embarked_filled 0
dtype: int64
Python
복사
sklearn 사용 결측치 처리
•
SimpleImputer; 치환
◦
파라미터
▪
missing_values: default값은 np.nan으로 비어있는 값을 채우게 되고 필요시 다른 값을 빈값으로 인식하게 할 수 있다.
▪
strategy: 채울 값에 대한 함수; mean, median, most_frequent, constant(따로 지정한 값)
▪
fill_value: strategy의 값이 constant일 때, 여기에 정의된 값으로 채움
from sklearn.impute import SimpleImputer
# strategy = mean, median, most_frequent
imputer = SimpleImputer(strategy="mean")
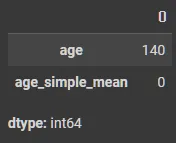
X_tr['age_simple_mean'] = imputer.fit_transform(X_tr[["age"]])
X_te['age_simple_mean'] = imputer.transform(X_te[["age"]])
X_tr[['age', 'age_simple_mean']].isnull().sum()
Python
복사
•
KNNImputer; 모델 기반
from sklearn.impute import KNNImputer
imputer = KNNImputer(n_neighbors=5)
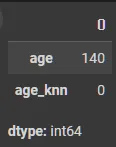
X_tr['age_knn'] = imputer.fit_transform(X_tr[["age"]])
X_te['age_knn'] = imputer.transform(X_te[["age"]])
X_tr[['age', 'age_knn']].isnull().sum()
Python
복사
•
IterativeImputer; 모델 기반
from sklearn.experimental import enable_iterative_imputer
from sklearn.impute import IterativeImputer
imputer = IterativeImputer(random_state=SEED)
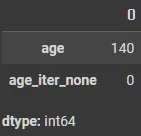
X_tr['age_iter_none'] = imputer.fit_transform(X_tr[["age"]])
X_te['age_iter_none'] = imputer.transform(X_te[["age"]])
X_tr[['age', 'age_iter_none']].isnull().sum()
Python
복사
from sklearn.ensemble import RandomForestRegressor
imputer = IterativeImputer(estimator=RandomForestRegressor(verbose=0, random_state=SEED),
max_iter=10, verbose=0, imputation_order='ascending', random_state=SEED)
X_tr['age_iter_none'] = imputer.fit_transform(X_tr[["age"]])
X_te['age_iter_none'] = imputer.transform(X_te[["age"]])
X_tr[['age', 'age_iter_none']].isnull().sum()
Python
복사
비대칭 데이터(옵션)
비대칭 데이터 확인
•
왜도
# 왜도
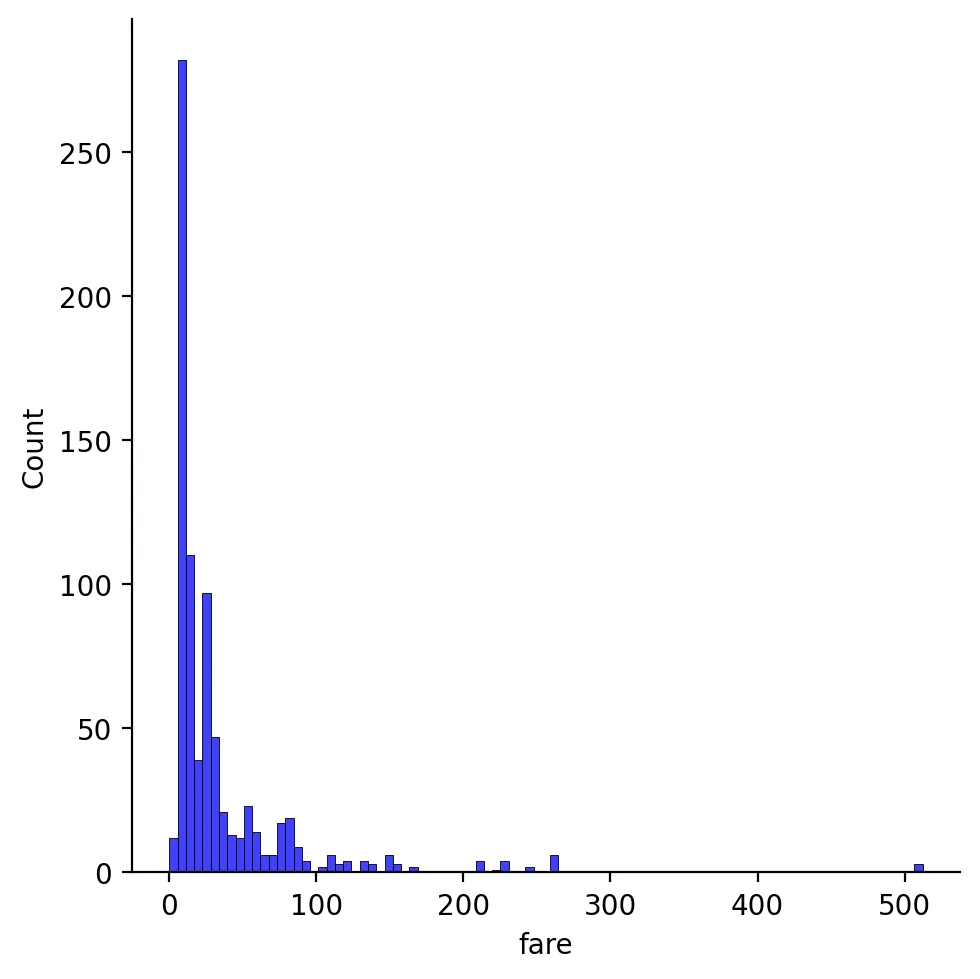
df['fare'].skew()
# 4.570768460673977
Python
복사
•
첨도
# 첨도
df['fare'].kurt()
# 30.20805166179377
Python
복사
•
그래프
sns.displot(df["fare"], color="b", label="Skewness : %.2f"%(df["fare"].skew()))
Python
복사
비대칭 데이터 처리
•
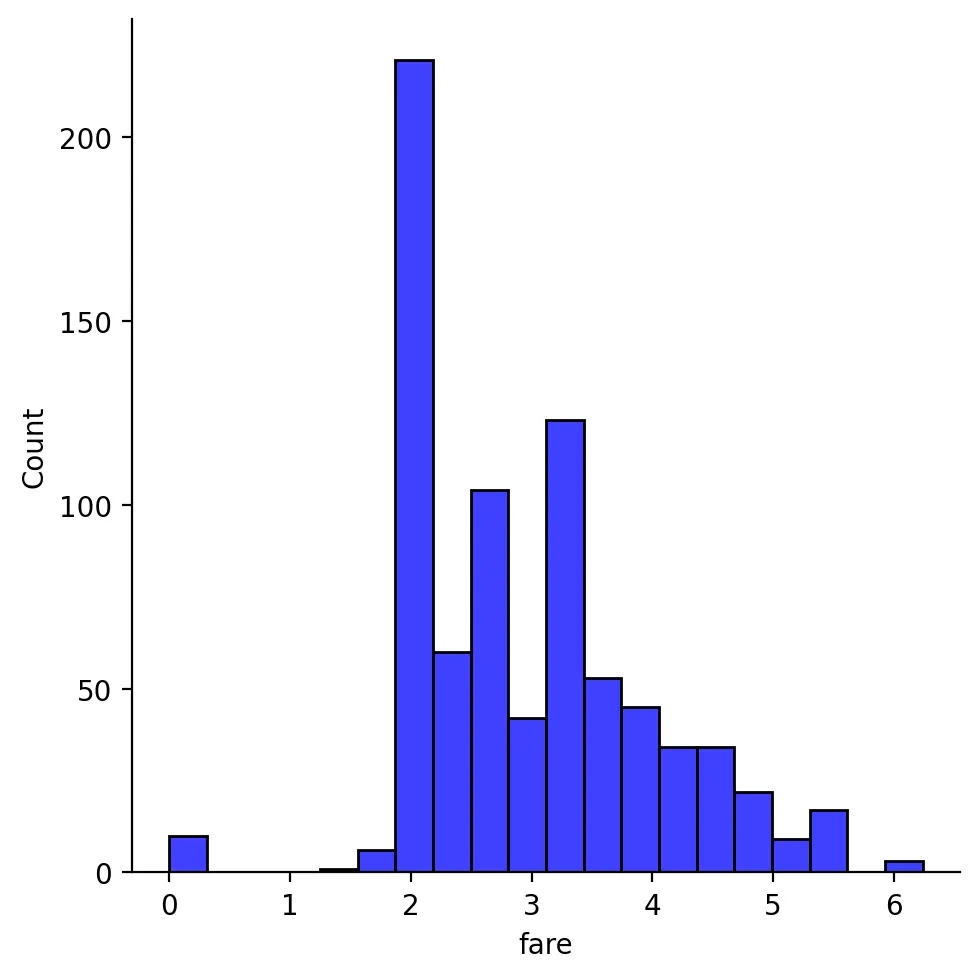
log 이용
df["fare"] = df["fare"].map(lambda i: np.log(i) if i > 0 else 0) # log를 이용하여 비대칭 처리
sns.displot(df["fare"], color="b", label="Skewness : %.2f"%(df["fare"].skew()))
Python
복사
•
krut()
df['fare'].skew(), df['fare'].kurt()
# (0.44180329763623455, 0.4696485867791105)
Python
복사
이상치(옵션)
이상치 확인
df['age'].skew(), df['age'].kurt()
# (0.3674542095476674, 0.09072738061837127)
Python
복사
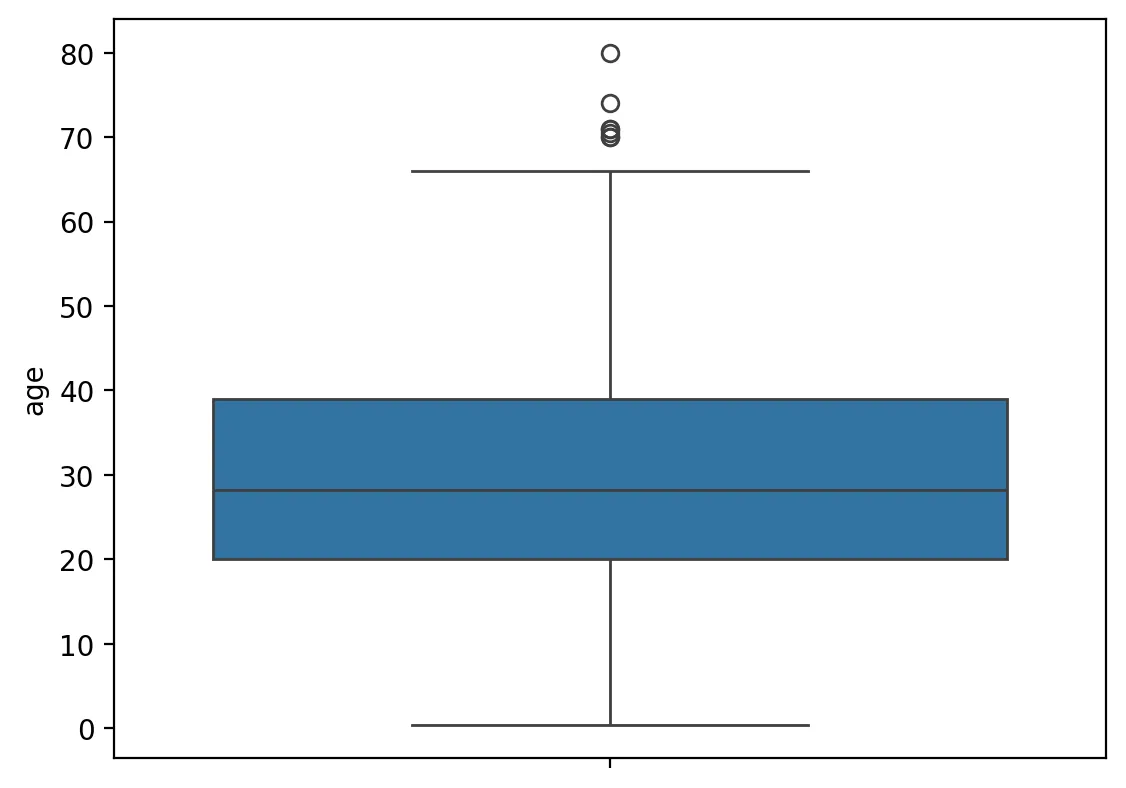
sns.boxplot(y=df['age'], data=df)
Python
복사
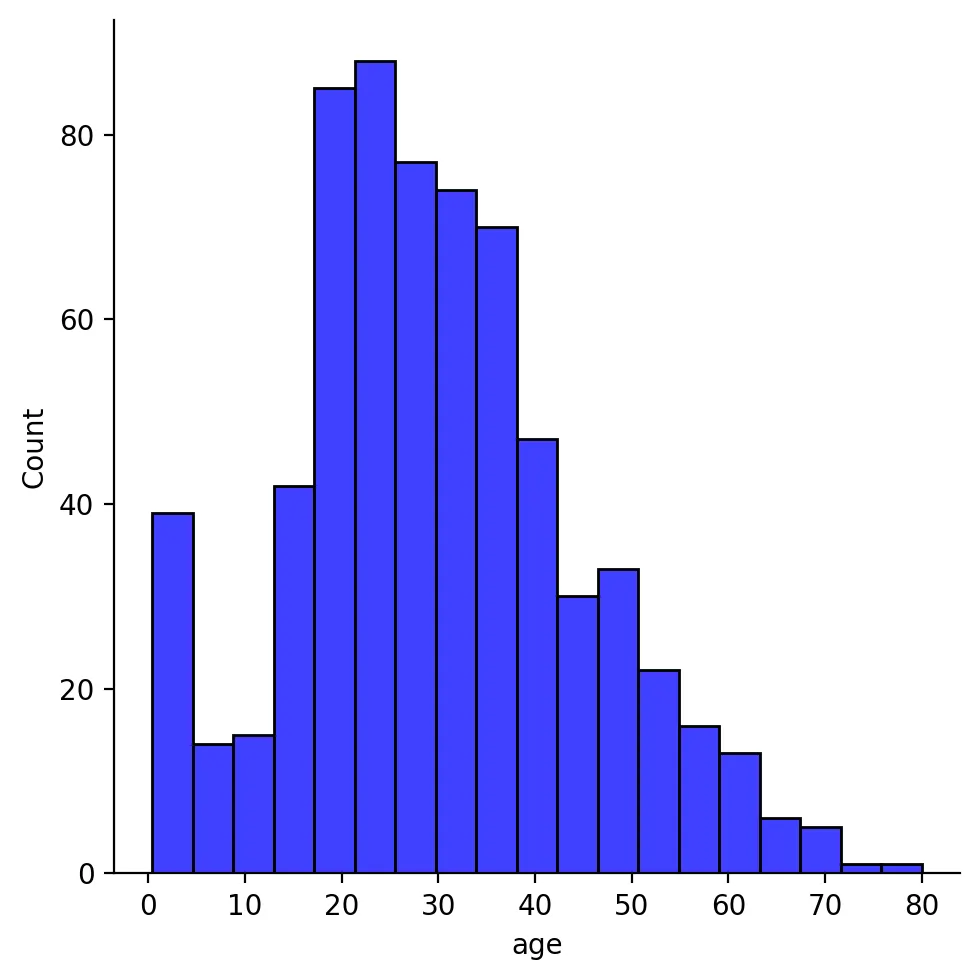
sns.displot(df["age"], color="b", label="Skewness : %.2f"%(df["age"].skew()))
Python
복사
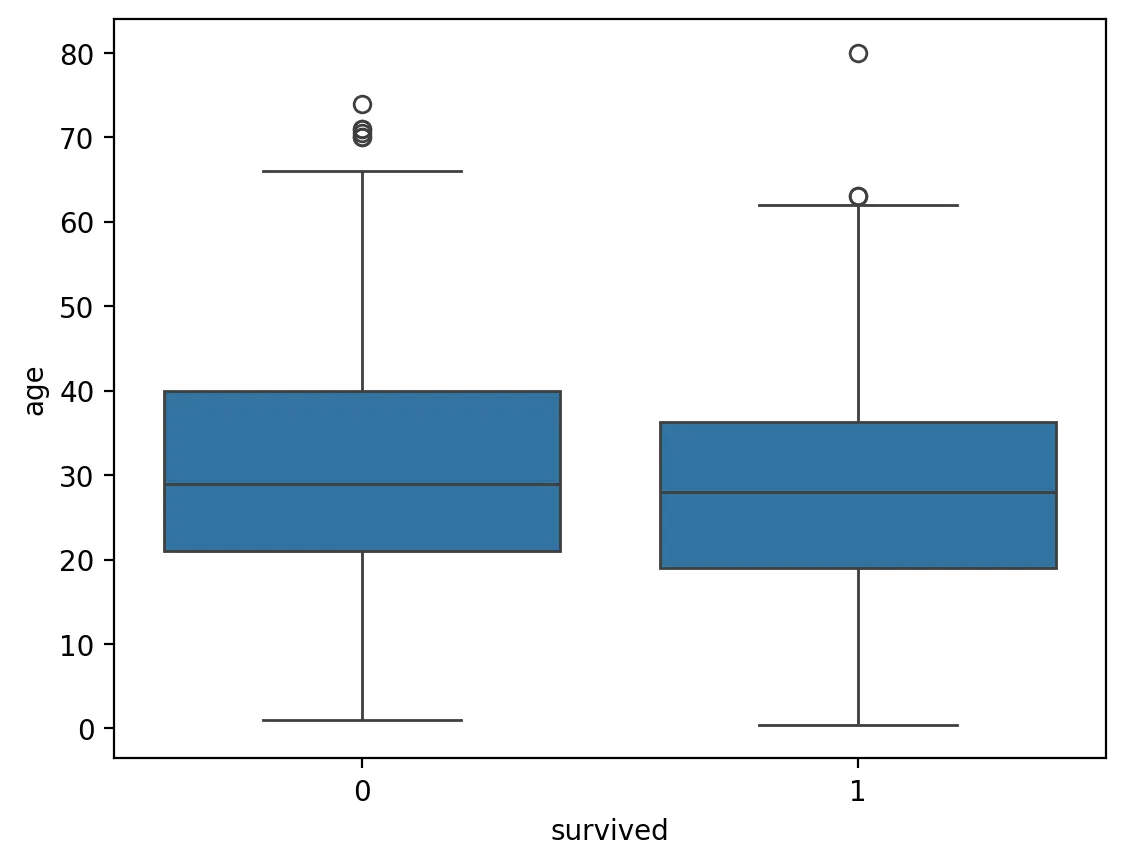
sns.boxplot(x=df['survived'], y=df['age'], data=df)
Python
복사
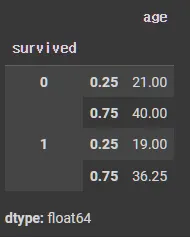
df.groupby(['survived'])['age'].quantile([0.25, 0.75]) # 분위수 계산
Python
복사
df['age'].quantile([0.25, 0.5, 0.75])
Python
복사
quantiles = df['age'].quantile([0.25, 0.75]).values
IQR = quantiles[1] - quantiles[0]
Upper_boundary = quantiles[1] + 1.5*IQR
Lower_boundary = quantiles[0] - 1.5*IQR
print('age outliers are values < {lowerboundary} or > {upperboundary}'.format(lowerboundary=Lower_boundary, upperboundary=Upper_boundary))
# age outliers are values < -8.5 or > 67.5
Python
복사
cond1 = df['age'] > Upper_boundary
cond2 = df['age'] < Lower_boundary
cond = cond1 | cond2
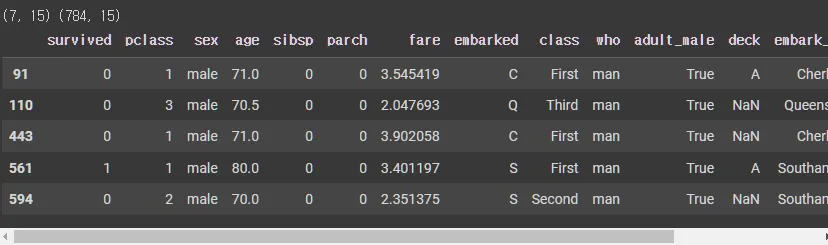
outlier = df.loc[cond]
print(outlier.shape, df.shape)
outlier.head()
Python
복사
c1 = outlier['age'] >= Lower_boundary
c2 = outlier['age'] <= Upper_boundary
c = c1 & c2
outlier.loc[c].shape
# (0, 15)
Python
복사
이상치 처리
df['age'] = df['age'].map(lambda x: Upper_boundary if x > Upper_boundary else x)
df['age'] = df['age'].map(lambda x: Lower_boundary if x < Lower_boundary else x)
Python
복사
cond1 = df['age'] > Upper_boundary
cond2 = df['age'] < Lower_boundary
cond = cond1 | cond2
outlier = df.loc[cond]
print(outlier.shape, df.shape)
outlier.head()
Python
복사
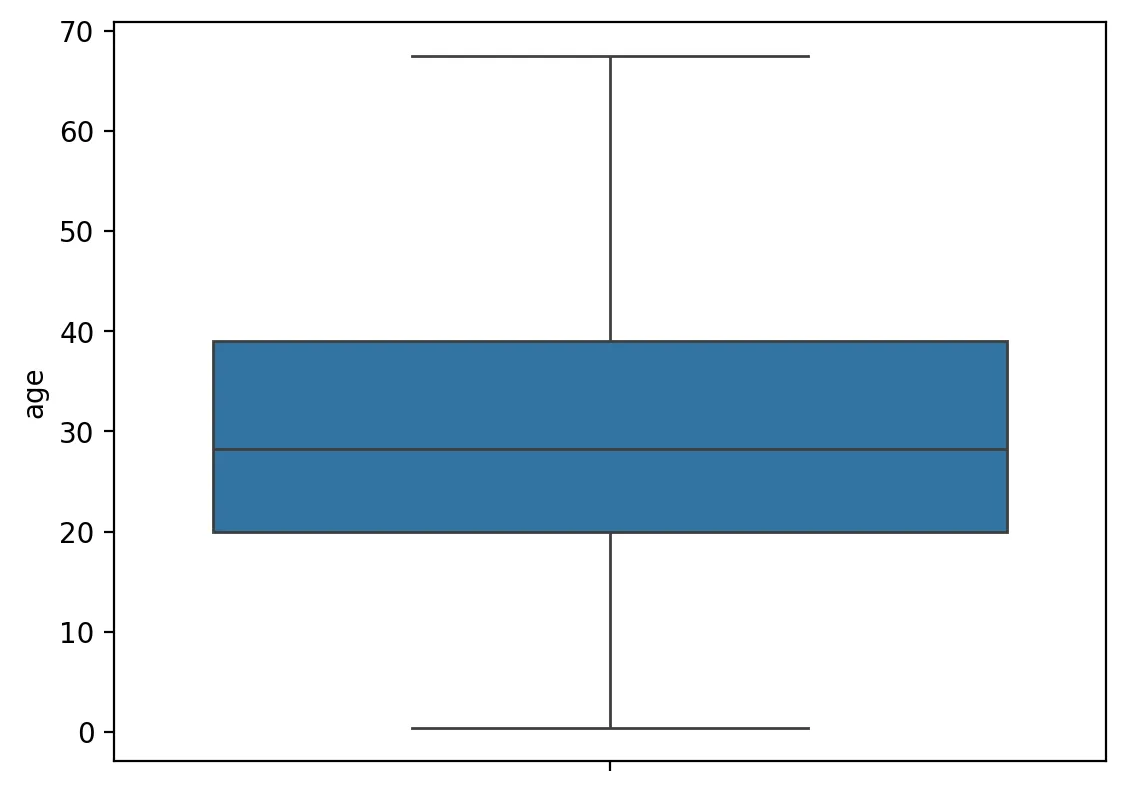
sns.boxplot(y=df['age'], data=df)
Python
복사
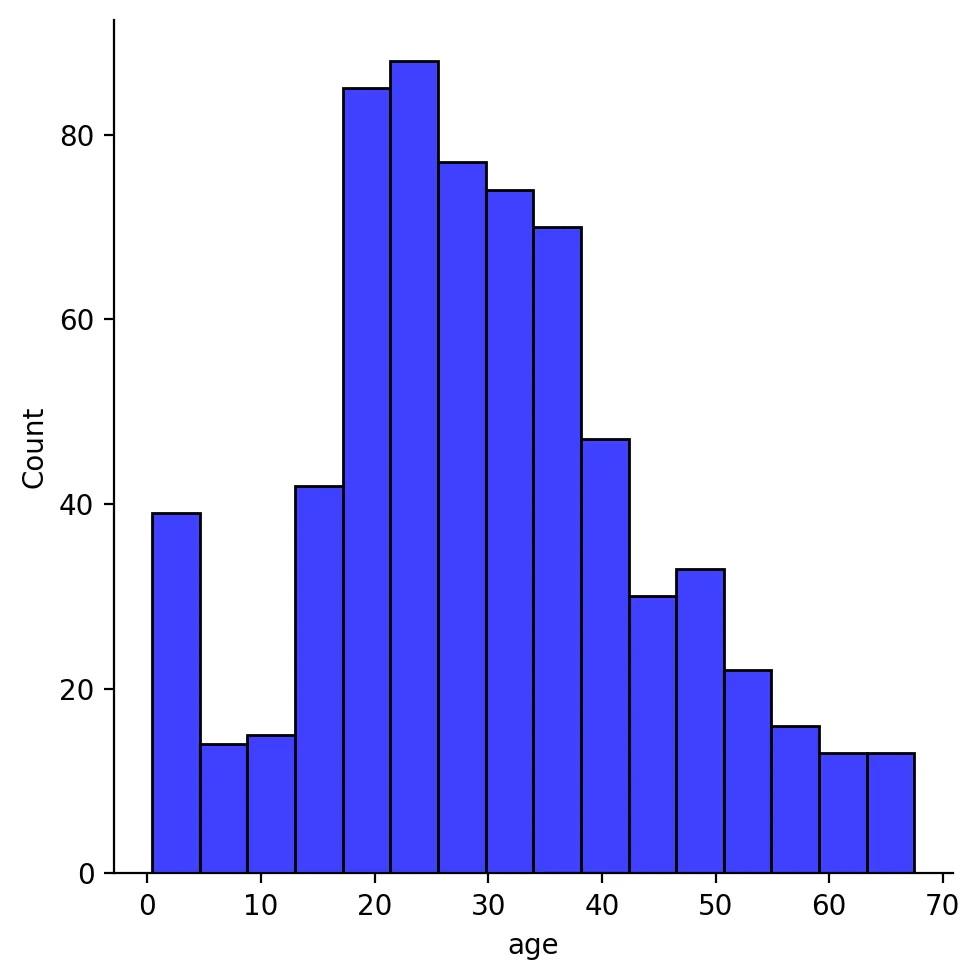
sns.displot(df["age"], color="b", label="Skewness : %.2f"%(df["age"].skew()))
Python
복사
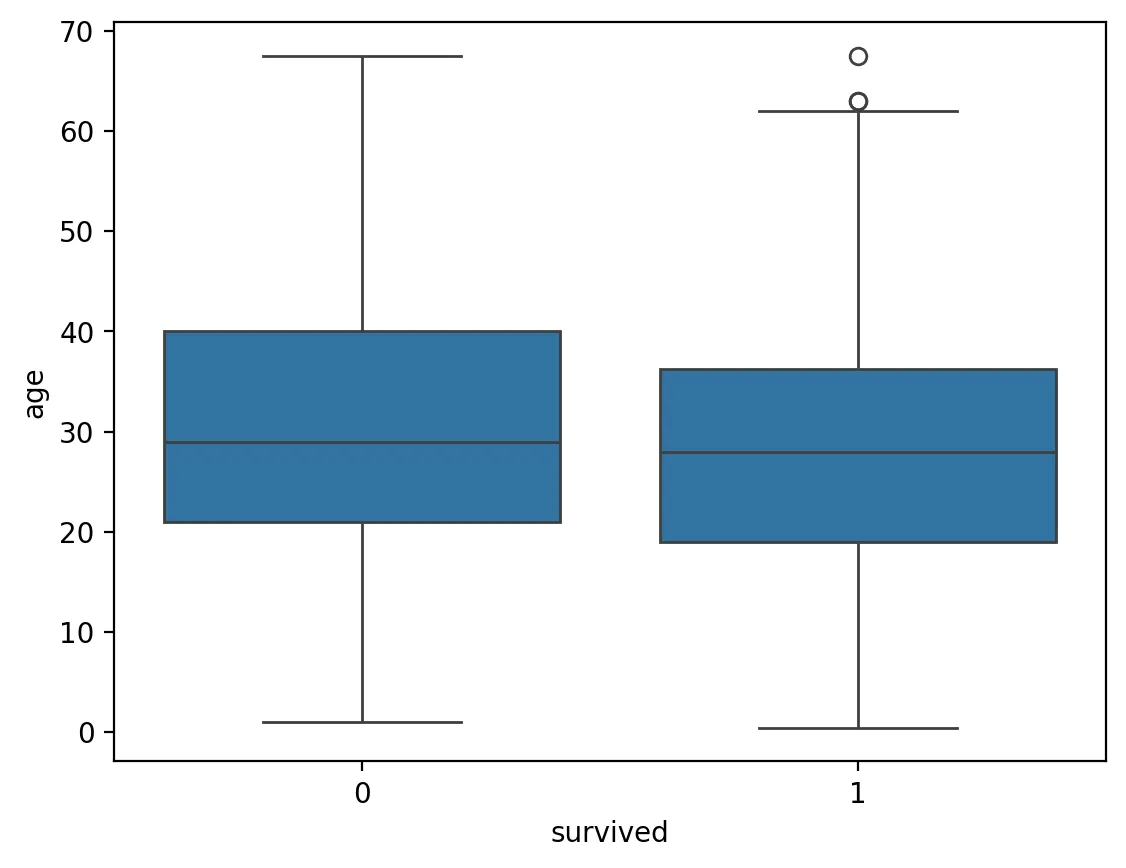
sns.boxplot(x=df['survived'], y=df['age'], data=df)
Python
복사