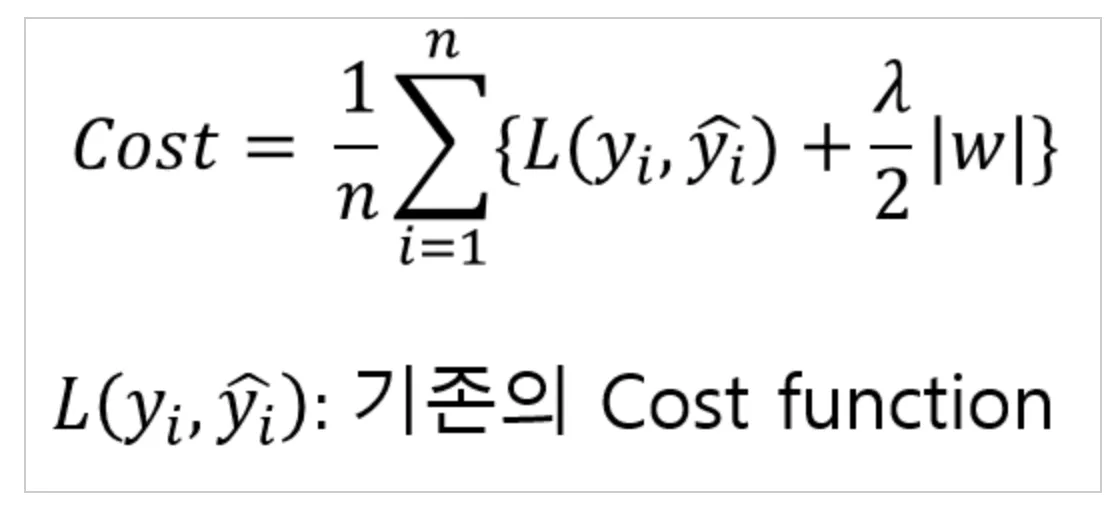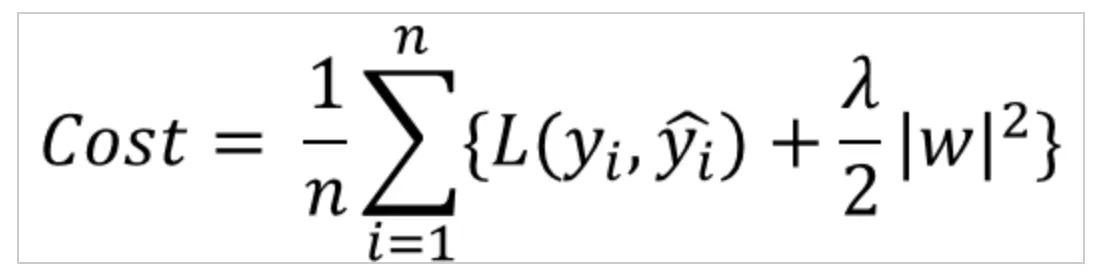예측 모델

import logging

logging.getLogger('matplotlib.font_manager').setLevel(logging.ERROR)

import mglearn

from sklearn.model_selection import train_test_split

import pandas as pd
import numpy as np

import matplotlib.pyplot as plt
import matplotlib as mpl
# import matplotlib.font_manager as fm
import seaborn as sns

# 브라우저에서 바로 그려지도록
%matplotlib inline
Python
복사

선형 회귀

•

수학적으로 생각해보면 어떤 요인의 수치에 따라서 특정 요인의 수치가 영향을 받고 있다고 말할 수 있다.

◦

시험 공부하는 시간을 늘리면 늘릴 수록 성적이 잘 나온다. 

◦

하루에 걷는 횟수를 늘릴 수록 몸무게는 줄어든다. 

•

다른 변수의 값을 변하게하는 변수를 x, 변수 x에 의해서 값이 종속적으로 변하는 변수 y라고 한다면, 변수 x의 값은 독립적으로 변할 수 있는 것에 반해, 변수 y값은 계속해서 x의 값에 의해서 종속적으로 결정되므로, x를 독립변수, y를 종속변수라고 한다.

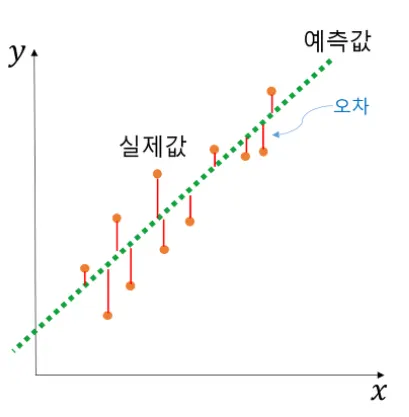
단순 선형 회귀 분석(Simple Linear Regression Analysis)

•

y=wx+by=wx+by=wx+b : 단순 선형 회귀의 수식

•

여기서 독립변수 x와 곱해지는 값 w를 머신러닝에서는 가중치(weight), 별도로 더해지는 값 b를 편향(bias)이라고 함.

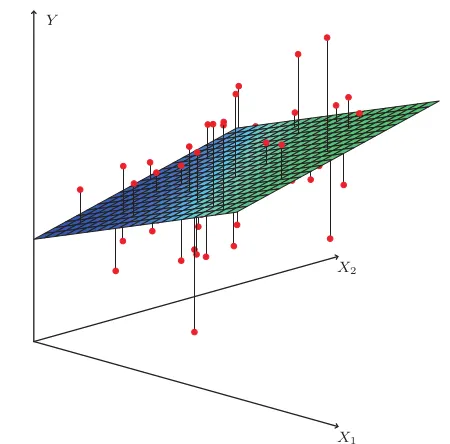
다중 선형 회귀 분석(Multiple Linear Regression Analysis)

y=w_1x_1+w_2x_2+...+w_nx_n+b

•

집의 매매 가격은 단순히 집의 평수가 크다고 결정되는 게 아니라 집의 층 수, 방의 개수, 지하철 역과의 거리 등에도 영향이 있다. 

•

이러한 다수의 요소를 가지고 집의 매매 가격을 예측할때 다중 선형 회귀 분석을 사용한다.

•

딥러닝 때도 자주 사용

정규화(Regularization)

•

모델을 학습할 때는 비용(cost) 즉, 오류를 최소화하는 방향으로 진행이 된다.

•

이 비용(cost) 또는 손실(loss)이 얼마나 있는지 나타내는 것이 비용함수(Cost Function), 손실함수(Loss Function)이라고 한다.

•

W(weight)가 너무 큰 값들을 가지지 않도록 하는 것이다.

•

W가 너무 큰 값을 가지게 되면 과하게 구불구불한 형태의 함수가 만들어지는데, Regularization은 이런 모델의 복잡도를 낮추기 위한 방법이다.

•

Regularization은 단순하게 cost function을 작아지는 쪽으로 학습하면 특정 가중치 값들이 커지면서 결과를 나쁘게 만들기 때문에 cost function을 바꾼다.

L1 Regularization : 마름모

•

가중치의 합을 더한 값에 learning rate(학습률) λ\lambdaλ를 곱하여 오차에 더한다.

•

L2 Norm은 각각의 벡터에 대해 항상 Unique한 값을 내지만, L1 Norm은 경우에 따라 특정 Feature 없이도 같은 값을 낼 수 있다. 

→ 즉, L1 Regularization은 Feature selection이 가능

•

이러한 특징 때문에 L1은 Sparse dataset에 적합

L2 Regularization : 원

•

각 가중치 제곱의 합에 learning rate(학습률) λ를 곱한다.

•

learning rate(학습률) λ를 크게 하면 가중치가 더 많이 감소되고,  λ를 작게 하면 가중치가 증가한다.

L2 규제가 L1 규제에 비해 더 안정적이라 일반적으로는 L2 규제가 더 많이 사용된다.

회귀의 선형 모델

LinearRegression (선형회귀)

•

최소제곱법(Ordinary Least Squares)을 활용.

•

실제값에서 예측값을 뺀 차이의 제곱에 합

\sum{(y_i - f(x_i))^2}

from sklearn.linear_model import LinearRegression
Python
복사

•

데이터 로드

X, y = mglearn.datasets.load_extended_boston()
print(f'{X.shape} / {y.shape}')
# (506, 104) / (506,)
# x = 104개 w도 104개여야함
Python
복사

•

데이터 분리(학습용, 테스트용)

X_tr, X_te, y_tr, y_te = train_test_split(X, y, test_size=0.25, random_state=0)
print(f'X_tr.shape: {X_tr.shape}')
# X_tr.shape: (379, 104)
Python
복사

•

선형 회귀 모델 정의

lr = LinearRegression()
Python
복사

•

모델 학습

lr.fit(X_tr, y_tr)
Python
복사

•

모델 학습 결과 확인

X_tr.shape, y_tr.shape
# ((379, 104), (379,))
Python
복사

print(f'bias: {lr.intercept_} / weights.shape: {lr.coef_.shape} \n\n  / weights: {lr.coef_}')

bias: 30.934563673643304 / weights.shape: (104,) 
# 모델의 파라미터들
  / weights: [-4.12710947e+02 -5.22432068e+01 -1.31898815e+02 -1.20041365e+01
 -1.55107129e+01  2.87163342e+01  5.47040992e+01 -4.95346659e+01
  2.65823927e+01  3.70620316e+01 -1.18281674e+01 -1.80581965e+01
 -1.95246830e+01  1.22025403e+01  2.98078144e+03  1.50084257e+03
  1.14187325e+02 -1.69700520e+01  4.09613691e+01 -2.42636646e+01
  5.76157466e+01  1.27812142e+03 -2.23986944e+03  2.22825472e+02
 -2.18201083e+00  4.29960320e+01 -1.33981515e+01 -1.93893485e+01
 -2.57541277e+00 -8.10130128e+01  9.66019367e+00  4.91423718e+00
 -8.12114800e-01 -7.64694179e+00  3.37837099e+01 -1.14464390e+01
  6.85083979e+01 -1.73753604e+01  4.28128204e+01  1.13988209e+00
 -7.72696840e-01  5.68255921e+01  1.42875996e+01  5.39551110e+01
 -3.21709644e+01  1.92709675e+01 -1.38852338e+01  6.06343266e+01
 -1.23153942e+01 -1.20041365e+01 -1.77243899e+01 -3.39868183e+01
  7.08999816e+00 -9.22538241e+00  1.71980268e+01 -1.27718431e+01
 -1.19727581e+01  5.73871915e+01 -1.75331865e+01  4.10103194e+00
  2.93666477e+01 -1.76611772e+01  7.84049424e+01 -3.19098015e+01
  4.81752461e+01 -3.95344813e+01  5.22959055e+00  2.19982410e+01
  2.56483934e+01 -4.99982035e+01  2.91457545e+01  8.94267456e+00
 -7.16599297e+01 -2.28147862e+01  8.40660981e+00 -5.37905422e+00
  1.20137322e+00 -5.20877186e+00  4.11452351e+01 -3.78250760e+01
 -2.67163851e+00 -2.55217108e+01 -3.33982030e+01  4.62272693e+01
 -2.41509169e+01 -1.77532970e+01 -1.39723701e+01 -2.35522208e+01
  3.68353800e+01 -9.46890859e+01  1.44302810e+02 -1.51158659e+01
 -1.49513436e+01 -2.87729579e+01 -3.17673192e+01  2.49551594e+01
 -1.84384534e+01  3.65073948e+00  1.73101122e+00  3.53617137e+01
  1.19553429e+01  6.77025947e-01  2.73452009e+00  3.03720012e+01]
Python
복사

•

학습한 모델을 이용한 검증 데이터 예측

pred = lr.predict(X_te)
pred[:5] 
# array([23.65294082, 26.73756431, 29.61078314, 10.15490293, 19.63821608])

X_te.shape, X_tr.shape
# ((127, 104), (379, 104))

pred.shape, y_te.shape, X_te.shape
# ((127,), (127,), (127, 104))
Python
복사

•

모델 평가

훈련용 평가지표는 0.95가 넘지만, 테스트용 평가지표는 0.61임으로 이 모델은 Overfitting 된 모델이다.

# 기본 평가지표는 결정계수이다. 결정계수는 0 ~ 1 사이 값을 갖으며, 1에 가까울 수록 정확도가 높다는 뜻이다.
print(f'훈련용 평가지표: {lr.score(X_tr, y_tr)} / 테스트용 평가지표: {lr.score(X_te, y_te)}')
# 훈련용 평가지표: 0.9520519609032728 / 테스트용 평가지표: 0.6074721959665773
# 학습데이터는 기가 막히게 잘 맞추지만 데이터가 조금만 달라져도 멍청이가 된다.
# 오버피팅을 엄청나게 하고 
Python
복사

Ridge with L2(제곱)

•

선형회귀에 L2 규제 적용

from sklearn.linear_model import Ridge

ridge = Ridge().fit(X_tr, y_tr)
Python
복사

L2 규제가 적용된 Ridge를 사용하여 훈련용 평가지표는 LinearRegression보다 낮지만, 테스트용 평가지표는 높은 것을 확인할 수 있다.

print(f'훈련용 평가지표: {ridge.score(X_tr, y_tr)} / 테스트용 평가지표: {ridge.score(X_te, y_te)}')

	# 훈련용 평가지표: 0.8857966585170941 / 테스트용 평가지표: 0.7527683481744751
Python
복사

◦

alpha 값을 낮추면 규제의 효과가 없어져 과대적합이 될 가능성이 높아진다.

◦

alpha 값을 높이면 훈련 세트의 성능은 나빠지지만 일반화에는 도움을 줄 수 있다.

•

실제로 훈련용 평가지표와 테스트용 평가지표의 차이가 줄어든 것을 확인할 수 있다.

ridge10 = Ridge(alpha=10).fit(X_tr, y_tr)
print(f'훈련용 평가지표: {ridge10.score(X_tr, y_tr)} / 테스트용 평가지표: {ridge10.score(X_te, y_te)}')
# 훈련용 평가지표: 0.7882787115369614 / 테스트용 평가지표: 0.635941148917731

ridge01 = Ridge(alpha=0.1).fit(X_tr, y_tr)
print(f'훈련용 평가지표: {ridge01.score(X_tr, y_tr)} / 테스트용 평가지표: {ridge01.score(X_te, y_te)}')
# 훈련용 평가지표: 0.9282273685001992 / 테스트용 평가지표: 0.7722067936479814
Python
복사

plt.figure(figsize=(10,8))

plt.plot(ridge10.coef_, '^', label='Ridge alpha=10')
plt.plot(ridge.coef_, 's', label='Ridge alpha=1')
plt.plot(ridge01.coef_, 'v', label='Ridge alpha=0.1')

plt.plot(lr.coef_, 'o', label='LinearRegression')

plt.xlabel('alpha list') # 계수 목록
plt.ylabel('alpha size') # 계수 크기
plt.hlines(0, 0, len(lr.coef_))
plt.ylim(-25, 25)
plt.legend()
Python
복사

◦

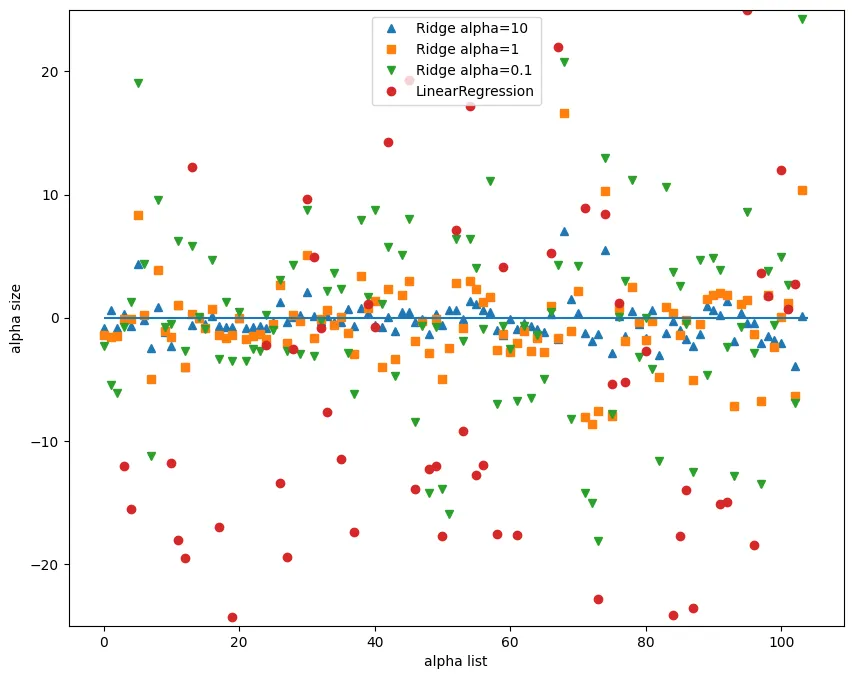
Ridge에서 alpha값이 클 수록 각각의 계수 크기가 작아지는 경향을 볼 수 있습니다. 따라서 L2 규제가 강해진다고 할 수 있으며, 이는 과적합이 될 가능성이 낮아진다는 뜻이다.

◦

하지만 aplha값을 아무리 높이더라도 Ridge의 계수크기가 0이 되지는 않는다.

mglearn.plots.plot_ridge_n_samples()
Python
복사

▪

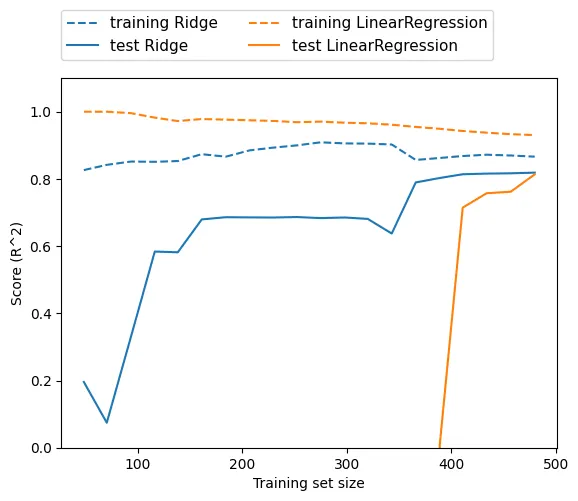
위의 그래프는 보스턴 주택가격 데이터셋에서 여러 가지 크기로 샘플링하여 LinearRegression과 Ridge를 적용한 것이다.

▪

여기서 배울 수 있는 것은 데이터를 충분히 주면 규제 항은 덜 중요해져서 릿지 회귀와 선형 회귀의 성능이 같아질 것이라는 점이다.

Lasso with L1(절대값)

•

L1 규제를 사용하면, 실제로 일부 피쳐들의 계수(weight)가 0이 된다. 

→ 이 말은 모델에서 완전히 제외되는 특성(피쳐)이 생긴다는 뜻이다.

•

일부 계수를 0으로 만들면 모델을 이해하기 쉬워지고 이 모델의 가장 중요한 특성이 무엇인지 드러내준다.

•

alpha값을 줄이면 가장 낮은 오차를 찾아가는 반복횟수(max_iter)가 늘어나야 한다.

from sklearn.linear_model import Lasso

lasso = Lasso().fit(X_tr, y_tr)
print(f'훈련용 평가지표: {lasso.score(X_tr, y_tr)} / 테스트용 평가지표: {lasso.score(X_te, y_te)}')
print('-'*80)
print(f'사용한 특성의 수: {np.sum(lasso.coef_ != 0)} / 전체 특성 수: {X_tr.shape[1]}')

# 훈련용 평가지표: 0.29323768991114607 / 테스트용 평가지표: 0.20937503255272294
# -------------------------------------------------------------------------------
# 사용한 특성의 수: 4 / 전체 특성 수: 104
Python
복사

# alpha값을 변경할 때는 max_iter를 증가 시켜야 한다.
lass001 = Lasso(alpha=0.01, max_iter=100000).fit(X_tr, y_tr)
print(f'훈련용 평가지표: {lass001.score(X_tr, y_tr)} / 테스트용 평가지표: {lass001.score(X_te, y_te)}')
print(f'사용한 특성의 수: {np.sum(lass001.coef_ != 0)} / 전체 특성 수: {X_tr.shape[1]}')

# 훈련용 평가지표: 0.8962226511086497 / 테스트용 평가지표: 0.7656571174549982
# 사용한 특성의 수: 33 / 전체 특성 수: 104
Python
복사

•

오버피팅 발생

lass00001 = Lasso(alpha=0.0001, max_iter=100000).fit(X_tr, y_tr)
print(f'훈련용 평가지표: {lass00001.score(X_tr, y_tr)} / 테스트용 평가지표: {lass00001.score(X_te, y_te)}')
print(f'사용한 특성의 수: {np.sum(lass00001.coef_ != 0)} / 전체 특성 수: {X_tr.shape[1]}')

# 훈련용 평가지표: 0.9507158754515463 / 테스트용 평가지표: 0.6437467421272821
# 사용한 특성의 수: 96 / 전체 특성 수: 104
Python
복사

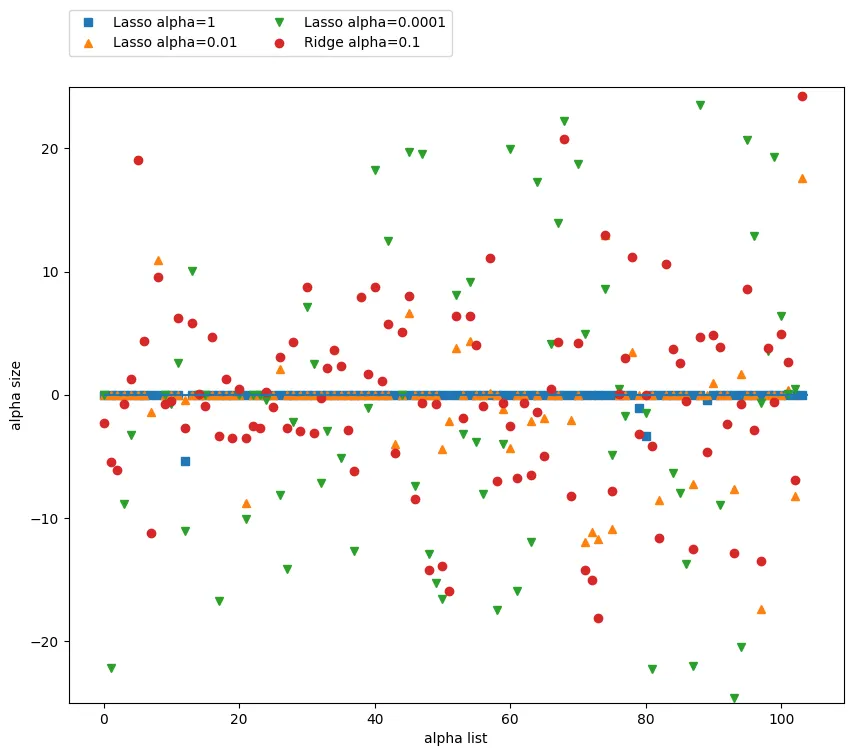
plt.figure(figsize=(10,8))

plt.plot(lasso.coef_, 's', label='Lasso alpha=1')
plt.plot(lass001.coef_, '^', label='Lasso alpha=0.01')
plt.plot(lass00001.coef_, 'v', label='Lasso alpha=0.0001')

plt.plot(ridge01.coef_, 'o', label='Ridge alpha=0.1')

plt.xlabel('alpha list') # 계수 목록
plt.ylabel('alpha size') # 계수 크기
plt.hlines(0, 0, len(lr.coef_))
plt.ylim(-25, 25)
plt.legend(ncol=2, loc=(0, 1.05))
Python
복사

ElasticNet

•

선형회귀에 L1규제, L2규제를 동시에 적용한 모델

•

주요 파라미터

◦

alpha: 규제 계수

◦

l1_ratio(default=0.5)

▪

0이면, L2 규제만

▪

1이면, L1 규제만

▪

0 < l1_ratio < 1이면, 혼합

from sklearn.linear_model import ElasticNet

elnet = ElasticNet().fit(X_tr, y_tr)
print(f'훈련용 평가지표: {elnet.score(X_tr, y_tr)} / 테스트용 평가지표: {elnet.score(X_te, y_te)}')
print(f'사용한 특성의 수: {np.sum(elnet.coef_ != 0)} / 전체 특성 수: {X_tr.shape[1]}')
# 훈련용 평가지표: 0.32837814485847916 / 테스트용 평가지표: 0.2217004367773664
# 사용한 특성의 수: 38 / 전체 특성 수: 104
Python
복사

•

수동 하이퍼파라미터 설정

alpha=0.01
ratios = [0.2, 0.5, 0.8]

for ratio in ratios:
  elnet = ElasticNet(alpha=alpha, l1_ratio=ratio, random_state=42).fit(X_tr, y_tr)
  print(f'ratio: {ratio}')
  print(f'훈련용 평가지표: {elnet.score(X_tr, y_tr)} / 테스트용 평가지표: {elnet.score(X_te, y_te)}')
  print(f'사용한 특성의 수: {np.sum(elnet.coef_ != 0)} / 전체 특성 수: {X_tr.shape[1]}')
  print('-'*50) 
  
# 훈련용 평가지표: 0.8421033820826037 / 테스트용 평가지표: 0.7055067157435387
# 사용한 특성의 수: 93 / 전체 특성 수: 104
# --------------------------------------------------
# ratio: 0.5
# 훈련용 평가지표: 0.8553665697077995 / 테스트용 평가지표: 0.7209054027265394
# 사용한 특성의 수: 84 / 전체 특성 수: 104
# --------------------------------------------------
# ratio: 0.8
#훈련용 평가지표: 0.8752442706471416 / 테스트용 평가지표: 0.741439523522267
# 사용한 특성의 수: 63 / 전체 특성 수: 104
# --------------------------------------------------
Python
복사

alphas=[0.001, 0.01, 0.1]
ratio = 0.8

for alpha in alphas:
  elnet = ElasticNet(alpha=alpha, l1_ratio=ratio, random_state=42).fit(X_tr, y_tr)
  print(f'alpha: {alpha}')
  print(f'훈련용 평가지표: {elnet.score(X_tr, y_tr)} / 테스트용 평가지표: {elnet.score(X_te, y_te)}')
  print(f'사용한 특성의 수: {np.sum(elnet.coef_ != 0)} / 전체 특성 수: {X_tr.shape[1]}')
  print('-'*50)
  
# alpha: 0.001
# 훈련용 평가지표: 0.9271504286329 / 테스트용 평가지표: 0.7813331506633265
# 사용한 특성의 수: 91 / 전체 특성 수: 104
# --------------------------------------------------
# model = cd_fast.enet_coordinate_descent(
# alpha: 0.01
# 훈련용 평가지표: 0.8752442706471416 / 테스트용 평가지표: 0.741439523522267
# 사용한 특성의 수: 63 / 전체 특성 수: 104
# --------------------------------------------------
# alpha: 0.1
# 훈련용 평가지표: 0.7399596108844948 / 테스트용 평가지표: 0.5768205411208096
# 사용한 특성의 수: 33 / 전체 특성 수: 104
# --------------------------------------------------
Python
복사