Search

전치 행렬과 대칭/대각/반대칭 행렬

대분류
인공지능/데이터
소분류
AI 수학
유형
선형 대수학
부유형
전치
대칭
대각
반대칭
주요 레퍼런스
https://wikidocs.net/214407
최종 편집 일시
2024/10/27 15:33
생성 일시
2024/07/15 08:32
13 more properties

전치 행렬 (Transpose Matrix) : 대각선 뒤집기

•
원래 행렬의 행과 열을 뒤바꾼 행렬
•
A의 i행 j열 원소를 a_ij라 할 때, 행렬 A의 전치행렬 A^T는 다음과 같다.
A=[a11a12⋯a1ma21a22⋯a2m⋮⋮⋱⋮an1an2⋯anm]A = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1m} \\ a_{21} & a_{22} & \cdots & a_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nm} \end{bmatrix}
AT=[a11a21⋯an1a12a22⋯an2⋮⋮⋱⋮a1ma2m⋯anm]A^T = \begin{bmatrix} a_{11} & a_{21} & \cdots & a_{n1} \\ a_{12} & a_{22} & \cdots & a_{n2} \\ \vdots & \vdots & \ddots & \vdots \\ a_{1m} & a_{2m} & \cdots & a_{nm} \end{bmatrix}
◦
A는 𝑛×𝑚크기의 행렬이며, 𝐴^𝑇는 𝑚×𝑛 크기의 전치행렬

전치행렬의 특징

1.
전치행렬의 전치행렬은 원래 행렬과 동일
(AT)T=A(A^T)^T = A
2.
두 행렬의 합의 전치는 각각의 전치행렬의 합과 동일
(𝐴+𝐵)𝑇=𝐴𝑇+𝐵𝑇(𝐴+𝐵)^𝑇=𝐴^𝑇+𝐵^𝑇
3.
상수 k를 곱한 행렬의 전치는 상수를 전치한 행렬에 곱한것과 동일
(𝑘𝐴)𝑇=𝑘𝐴𝑇(𝑘𝐴)^𝑇=𝑘𝐴^𝑇
4.
두 행렬의 곱의 전치는 각각의 전치행렬을 역순으로 곱한 것과 동일
행렬의 곱에 전치행렬을 취하면 순서가 역순으로 변경
(𝐴𝐵)𝑇=𝐵𝑇𝐴𝑇(𝐴𝐵)^𝑇=𝐵^𝑇𝐴^𝑇

Python 코드 예시 (NumPy 활용)

import numpy as np # 행렬 생성 matrix = np.array([[1, 2, 3], [4, 5, 6]]) # 전치행렬 계산 transpose_matrix = np.transpose(matrix) print("원래 행렬:") print(matrix) print("전치행렬:") print(transpose_matrix)
Python
복사

대칭/대각 행렬

대칭 행렬(Symmetric Matrix) : 대각선 거울

•
전치(transpose)한 행렬과 원래 행렬이 같은 행렬
•
행렬의 대각선()을 기준으로 대칭되는 원소들이 같은 값을 가지는 행렬
•
주로 실수들로 구성되며, 중복된 정보를 가지고 있는 경우에 주로 사용
A=[abcbdecef]A = \begin{bmatrix} a & b & c \\ b & d & e \\ c & e & f \end{bmatrix}
◦
A_ij와 A_ji의 값이 동일 (i와 j는 행렬의 행과 열의 index)

대각 행렬 (Diagonal Matrix) : 중앙값 제외 값 0

•
대각선 상의 원소 이외의 원소가 모두 0인 행렬
•
다양한 수학적 연산과 변환을 표현할 때 사용
D=[d1000d2000d3]D = \begin{bmatrix} d_1 & 0 & 0 \\ 0 & d_2 & 0 \\ 0 & 0 & d_3 \end{bmatrix}
◦
대각선 외의 원소는 모두 0

Python 코드 예시 (NumPy 활용)

import numpy as np # 대칭행렬 생성 symmetric_matrix = np.array([[1, 2, 3], [2, 4, 5], [3, 5, 6]]) print("대칭행렬:") print(symmetric_matrix) 대칭행렬: [[1 2 3] [2 4 5] [3 5 6]] # 대각행렬 생성 diagonal_matrix = np.diag([2, 5, 8]) print("대각행렬:") print(diagonal_matrix) 대각행렬: [[2 0 0] [0 5 0] [0 0 8]]
Python
복사

반대칭 행렬(Skew-Symmetric Matrix)

•
전치행렬이 원래 행렬의 음수인 행렬
A=−ATA = -A^T

특징

1.
대각원소는 모두 0
aii=0a_{ii}=0
2.
다른 모든 원소에 대해 해당 수식 성립
aij=−aija_{ij} = -a_{ij}

예시

A=[0−2−320−5350]A = \begin{bmatrix} 0 & -2 & -3 \\ 2 & 0 & -5 \\ 3 & 5 & 0 \end{bmatrix}

계산하기

•
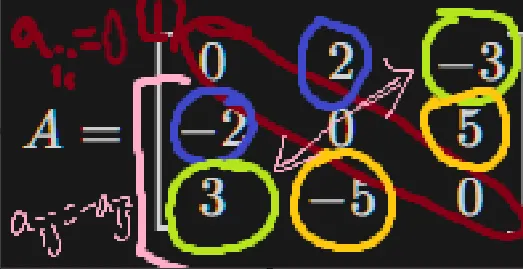
행렬 A에 대하여
A=[02−3−2053−50]A = \begin{bmatrix} 0 & 2 & -3 \\ -2 & 0 & 5 \\ 3 & -5 & 0 \end{bmatrix}
◦
행렬 A가 skew-symmetric하려면 해당 조건을 만족해야함
1.
대각 원소가 모두 0
•
대각 원소가 모두 (1,1), (2,2), (3,3) 모두 0 (Satisfied)
2.
대각 원소가 아닌 원소들에 대해 a_{ij} = -a_{ij}만족
a.
𝑎_{12}=2, −𝑎_{21}=−(−2)=2,  (Satisfied)
b.
𝑎_{13}=−3 , −𝑎_{31}=−3 (Satisfied)
c.
𝑎_{23}=5 ,  −𝑎{32}=−5 (Satisfied)
▪
모든 조건을 만족하므로, 행렬 A는 skew-symmetric 함

Skew-Symmetric Matrix의 활용

•
회전 변환과 관련된 문제에서 자주 활용
•
특정 물리적 시스템에서 나타나는 변환을 모델링하는 데에도 사용 가능

Python 코드 예시 (NumPy 활용)

import numpy as np # Given matrix A A = np.array([[0, 2, -3], [-2, 0, 5], [3, -5, 0]]) # Calculate the transpose of A A_transpose = A.T # Calculate the skew-symmetric matrix (-A_transpose) skew_symmetric_matrix = -A_transpose print("Given Matrix A:") print(A) Given Matrix A: [[ 0 2 -3] [-2 0 5] [ 3 -5 0]] print("\nTranspose of Matrix A:") print(A_transpose) Transpose of Matrix A: [[ 0 -2 3] [ 2 0 -5] [-3 5 0]] print("\nSkew-Symmetric Matrix:") print(skew_symmetric_matrix) Skew-Symmetric Matrix: [[ 0 2 -3] [-2 0 5] [ 3 -5 0]]
Python
복사